Внедрение федеральных государственных образовательных стандартов требует изменения целей образования. Применение системно-деятельностного подхода в процессе обучения учащихся решению сюжетных задач по математике позволяет выделить универсальные учебные действия, которыми должны овладеть ученики на данном этапе обучения.
Цель исследования
Разработка методических рекомендаций по реализации системно-деятельностного подхода в обучении учащихся решению сюжетных задач по математике.
Материал и методы исследования
Системно-деятельностный подход позволяет сформировать у школьников готовность к саморазвитию и самообразованию, способствует активизации познавательной деятельности учащихся.
Системный подход предполагает рассмотрение сложного объекта как системы. Изучение сюжетных задач можно строить как изучение некоторых систем.
В федеральном государственном образовательном стандарте определены требования к результатам, которые должны быть освоены обучающимися основной образовательной программы основного общего образования. В стандарте выделены требования к личностным, метапредметным и предметным результатам [1].
Метапредметные результаты включают освоенные обучающимися межпредметные понятия и универсальные учебные действия, способность их использования в учебной, познавательной и социальной практике, самостоятельность планирования и осуществления учебной деятельности и организации учебного сотрудничества с педагогами и сверстниками, построение индивидуальной образовательной траектории [1].
Для основного общего образования разработана программа развития универсальных учебных действий, в которой выделены следующие универсальные учебные действия: личностные, регулятивные, познавательные, коммуникативные [2].
В познавательные универсальные учебные действия включаются общеучебные действия, в частности знаково-символические; логические и действия постановки и решения проблем [2].
Действия, связанные с переработкой учебной информации, относят к познавательным общеучебным универсальным учебным действиям. В результате преобразования учебной информации в курсе математики получают различные учебные модели. В процессе обучения решению сюжетных задач получают следующие модели: схемы поиска решения сюжетной задачи, знаковая модель записи решения сюжетной задачи, алгоритм для решения задач, имеющих одинаковую структуру решения [3].
При обучении учеников решению сюжетных задач их необходимо познакомить с понятием графа, сформировать умения строить и описывать графовую модель. Эта деятельность связана с методом моделирования.
Моделирование – процесс создания модели. Моделирование устанавливает отношения между объектом, выбранным в качестве модели, и объектом, для которого он является моделью [4].
Результаты исследования и их обсуждение
Рассмотрим возможности развития познавательных универсальных учебных действий учащихся на примере обучения решению сюжетных задач. Задачи этого типа входят в состав ИГА, ЕГЭ и вызывают затруднения у учащихся.
В процессе решения сюжетной задачи ученик должен выполнить поставленные в задаче требования. Необходимо выявить зависимости между элементами сюжетной задачи, выразить их с помощью определенных действий, получить новые данные, использовать их в дальнейшем.
Трудности выполнения анализа условия задачи обусловлены тем, что существует разрыв между ситуацией, представленной в задаче, и ее математической моделью. Поэтому для осуществления анализа задачи ученикам можно предложить использовать графовые модели.
Построение графовых моделей помогает выделить элементы сюжетной задачи, установить связи и отношения между элементами.
В процессе решения сюжетной задачи ученики строят различные модели, которые соответствуют переформулированиям задачи.
При формировании у школьников умения проводить поиск решения сюжетной задачи необходимо выявление структуры решения задачи. Знание структуры позволяет оценивать сложность решения сюжетной задачи. Эта характеристика позволяет провести систематизацию задач по сложности их решения [5].
В процессе анализа сюжетных задач в школьных учебниках были выделены следующие виды отношений: отношение зависимости: c = a • b, отношение разностного (кратного) сравнения: a2 = a1 + d (a2 = a1 • d), отношение суммирования (вычитания): a = a1+ a2 (a = a1 - a2).
На рис. 1 представлены графы, которые являются простейшими.
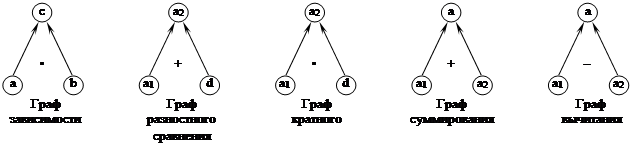
Рис. 1. Простейшие графы
Графы для более сложных задач строятся с использованием этих простейших графов.
В методике обучения математике используют общую схему, которая включает в себя следующие этапы решения задачи:
1. На первом этапе происходит понимание постановки задачи.
2. На втором этапе ученики получают план решения задачи.
3. На третьем этапе происходит осуществление плана решения задачи.
4. На четвертом этапе проводится анализ результатов решения задачи.
Используя эти этапы, выделяют соответствующие этапы графового моделирования:
1. Разбор задачи. На данном этапе выявляются структурные элементы решения задачи.
2. Описание задачи. На втором этапе устанавливаются связи и отношения между элементами.
3. Графовое моделирование решения задачи. На этом этапе происходит построение графовой модели.
4. Составление знаковой решающей модели. На четвертом этапе, с использованием графовой модели, составляется знаковая модель решения задачи.
5. Решение полученной модели. На данном этапе ученики получают решение задачи, подставляя известные значения величин.
6. Анализ результатов решения. На этом этапе целесообразно составить взаимно обратные задачи.
Покажем на примере обучения решению сюжетной задачи реализацию структурных элементов графового моделирования.
Задача 1. Два токаря выполнили заказ, изготовив 296 деталей. Один токарь изготавливал 10 деталей в день, а другой – 12 деталей. За сколько дней закончил работу второй токарь, если первый токарь работал 14 дней?
Разбор задачи показывает, что в задаче представлены две ситуации. В каждой ситуации рассматриваются три величины: с – объем работы, а – производительность, в – время. Между этими тремя величинами устанавливается отношение зависимости. Между величинами объема работы устанавливается отношение суммирования.
Представим структуру решения задачи на рис. 2.
с деталей – объем совместной работы,
с1 деталей – объем работы, выполненной первым токарем,
с2 деталей – объем работы, выполненной вторым токарем,
а1 деталей/день – производительность первого токаря,
а2 деталей/день – производительность второго токаря,
b1 дней – время работы первого токаря,
b2 дней – время работы второго токаря.
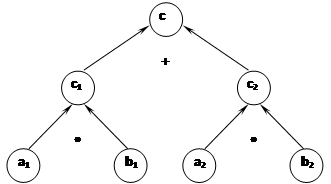
Рис. 2. Структура решения задачи 1
Составим знаковую решающую модель задачи:
1) 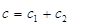
2) 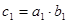
3) 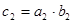
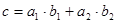
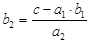
С помощью графовой модели можно получить алгоритм решения задачи.
Решение задачи методом составления уравнения можно получить, если «описывать» граф «снизу вверх».
Граф является обобщенной моделью решения задач различных сюжетов, в которых имеются те же отношения между величинами.
Из знаковой решающей модели можно получить взаимно обратные задачи:
1) 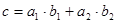
2) 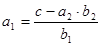
3) 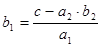
4) 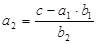
Решение взаимно обратных задач требует использования еще одного учебного действия. Это действие перемоделирования с помощью тождественных преобразований.
В качестве задания можно предложить ученикам составить задачи, решения которых можно представить в виде аналогичной графовой модели.
Рассмотрим примеры задач.
Задача 2. Турист первую часть пути проехал 2 часа на автобусе, скорость которого 60 км/ч, а вторую часть пути продолжал со скоростью 5 км/ч и затратил 0,5 часа. Какое расстояние турист преодолел за это время?
Задача 3. В кассе театра продано 120 билетов по 400 рублей и 80 билетов по 600 р. Сколько денег получено за все билеты?
Задача 4. В магазин привезли 15 ящиков картофеля, по 10 килограммов в каждом, и 7аящиков огурцов, по 12 килограммов в каждом. Найти массу товара, который привезли в магазин.
Задача 5. На стройке работало 4 бригады, по 25 человек в каждой, и 5 бригад, по 32ачеловека в каждой. Сколько человек работало на стройке?
Используя отношения разностного и кратного сравнения, можно получить задачи с усложненной структурой решения.
Задача 6. Две бригады изготовили 40 деталей. Первая бригада изготавливала 7 деталей в час, вторая – 4 детали в час. За сколько времени выполнила работу первая бригада, если известно, что вторая бригада работала на 1 час меньше первой бригады?
На рис. 3 представлена графовая модель решения задачи. Результат разностного сравнения: d часов.
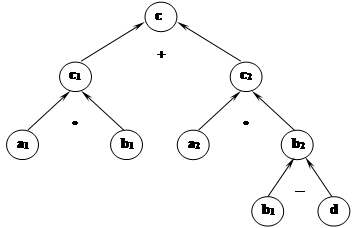
Рис. 3. Структура решения задачи 6
Задача 7. За 3 ч езды на автобусе и 8 ч езды на электропоезде туристы проехали 810 км. Определить скорость электропоезда, если известно, что она на 5 км/ч больше скорости автобуса?
На рис. 4 представлена структура решения задачи.
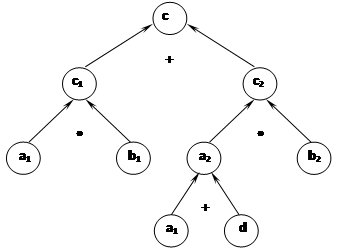
Рис. 4. Структура решения задачи 7
Рассмотрим пример задачи на кратное сравнение.
Задача 8. За 2 кг конфет и 3 кг печенья заплатили 1050 р. Сколько стоит 1 кг конфет, если он в 2 раза дороже 1 кг печенья?
На рис. 5 представлена графовая модель решения задачи.
При обучении учащихся решению сюжетных задач использование графовых моделей дает возможность выделить все элементы сюжетной задачи и установить отношения между элементами.
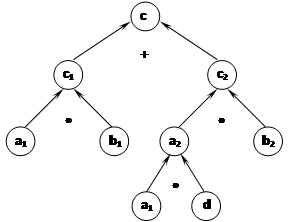
Рис. 5. Структура решения задачи 8
Построение графовой модели структуры решения сюжетной задачи помогает учащимся правильно провести анализ задачи, представить ход решения задачи в виде алгоритмического предписания и выбрать рациональный способ решения задачи.
Заключение
Таким образом, развитие познавательных универсальных учебных действий учащихся в процессе обучения решению сюжетных задач с использованием графового моделирования способствует активизации самостоятельной деятельности учащихся, что соответствует системно-деятельностному подходу в обучении.



