К важнейшим из компетенций будущего учителя относятся компетенции, позволяющие сформировать у него навыки составления задач. В статье обоснована необходимость обучения студентов, будущих учителей математики, методам составления задач.
Цель исследования: провести анализ методов составления задач, выделить наиболее подходящие из них для преподавания математики (представлены три из выделенных методов), проанализировав опыт обучения студентов приемам решения задач.
Материал и методы исследования. Одним из направлений подготовки учеников к Единому государственному экзамену является отработка навыков тестовой проверки знаний учащихся, что требует от учителя создания обширных классов однотипных задач, позволяющих формировать различные варианты равнозначных по уровню сложности тестов. Мощность каждого созданного класса задач коррелируется с числом вариантов одного уровня сложности, которые можно предложить учащимся. Тестовая проверка знаний учащихся позволяет осуществить контрольно-диагностический анализ уровня усвоения материала, может осуществляться для обучающих и тренировочных целей. Но как составить хотя бы необходимый минимум задач, не обременяя учителя многовариантной проверкой работ учащихся? Как помочь учителю в осуществлении этих идей? Для этого необходимо вооружить педагога знаниями методов составления задач. В поддержку нашего тезиса выступает и недостаточное на сегодняшний день количество систематизированных сборников задач, и доступность для ученика решения не авторской задачи в Интернете [1].
Второй, не менее важный, аргумент в пользу важности овладения навыками составления задач сводится к более глубокому пониманию метода решения задач данного типа. Отработка навыка решений задач данного класса не будет полной, если ученик не поймет специфики формулировки задач, решаемых данным методом. Умение составить задачу с прогнозируемым методом решения свидетельствует о глубоком понимании и проникновении в суть метода решения задач данного класса.
Обосновывая необходимость обучения студентов педагогических специальностей методам составления задач, можно воспользоваться принципом дополнительности, предложенным Г.Г. Гранатовым. Из всех постулатов этого принципа воспользуемся тем, что в любом педагогическом явлении должны присутствовать пары взаимодополняющих элементов. Для наиболее эффективного усвоения метода решения задачи необходимо усвоение умений и навыков создания задач, решаемых этим методом. Третий аргумент необходимости обучения методам составления задач сводится к развитию математического творчества, пониманию возможностей математики при решении прикладных, возможно даже производственных задач, составленных учащимися [2].
Мы выделяем следующие приемы формирования новых задач, которыми должны овладеть учителя:
1. Составление задач с заданным методом решения в общем виде.
2. Отыскание подзадач прямой задачи, их формулировка и решение.
3. Составление прикладных задач с использованием подбора необходимых и достаточных условий анализируемой ситуации, исключения лишних требований, дополнение данных по неполной ситуации [3].
4. Создание однотипных задач с вариативными численными данными.
5. Введение параметра при решении задачи и дальнейшая его конкретизация при составлении класса задач с прогнозируемыми свойствами решений.
6. Составление задачи по общей схеме краткой записи условия [4].
7. Составление обратных задач.
8. Формулировка вопросов к так называемой открытой задаче, методы составления открытых задач [5].
Результаты исследования и их обсуждение. Остановимся на некоторых из них. Рассмотрим способ введения параметра при решении задачи и дальнейшей его конкретизации для получения класса задач с прогнозируемым свойством решений.
Большие возможности в составлении задач предоставляют нам задачи с параметром. Рассмотрим для примера следующую задачу: «Решите уравнение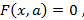 
где a – параметр». Ясно, что при каждом значении параметра мы получаем формулу решений или доказываем, что уравнений не имеет решений. Решив данное уравнение, мы будем иметь большие возможности в составлении новых задач. Для этого достаточно вместо параметра подставить конкретное число. И в зависимости от того, в какой диапазон попало это число, мы получаем формулу решения или будем иметь уравнение, которое не имеет решений. Таким образом, научив студентов решать задачи с параметрами, мы вооружаем их эффективным приемом составления задач, не содержащих параметр, заранее удовлетворяющих необходимым на данном этапе обучения свойствам. Заметим, что компиляцию задач на этом уровне можно поручить и электронным средствам [6].
Рассмотрим этот прием на простейшем примере. При отработке со студентами методики обучения учащихся решению квадратных уравнений для получения много вариативных ответов можно ввести в квадратное уравнение один или несколько параметров. Решить его, а затем, используя конкретизацию параметров, получить много однотипных задач с заданными ограничениями на решения. Сформулированный ответ позволяет составить серию квадратных уравнений предложенного вида, имеющих два решения, единственное решение и не имеющих решений. Для этого необходимо взять конкретные значения параметров, удовлетворяющих соответствующим ограничениям в ответе. Кроме того, мы имеем общую формулу решений, позволяющую быстро проверить правильность ответов учащихся.
Особое место с точки зрения дидактики изучения методов решения задач занимает составление задач с заданным методом решения в общем виде [6; 7].
Рассмотрим этот метод на примере изучения темы «Использование свойств функций при решении уравнений и неравенств». После актуализации со студентами приемов использования монотонности функций при решении уравнений и неравенств, мы формулируем следующую теорему.
Теорема. Пусть функция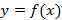 
определена на некотором промежутке Х.
Тогда
А. Если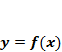 
монотонна на промежутке Х, то справедлив равносильный переход
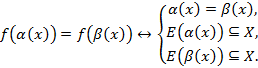
В. Если 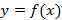возрастает на промежутке X, то
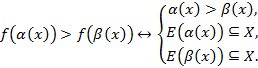
С. Если 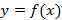убывает на промежутке X, то
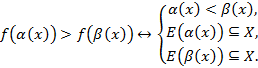
Студентам предлагается сформулировать алгоритм решения уравнений и неравенств с использованием представленной теоремы.
Алгоритм.
1. Ввести функцию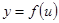 
.
2. Определить вид функций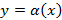 
и 
.
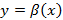3. Записать уравнение (неравенство) в виде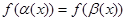 
( 
).
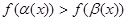4. Исследовать функцию :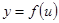
А. Найти область определения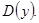 
Б. Определить характер монотонности, используя свойства монотонных функций или исследование монотонности функции при помощи производной.
В. Сделать вывод о возможности применения метода.
5. Применив теорему, получить соответствующую систему уравнений и неравенств.
6. Решить полученную систему. Записать ответ.
Студентам предлагается решить следующие уравнения и неравенства:
1. 
.
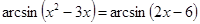2. 
.
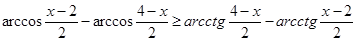3. 
.
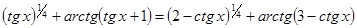4. 
.
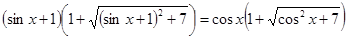Только после отработки метода решения предлагается придумать алгоритм, позволяющий составлять задания, решаемые данным способом:
1. Задать монотонную на множестве X функцию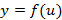 
.
2. Подобрать функци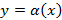и и .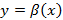
3. Представить уравнение (неравенство) в виде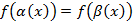 
(
).
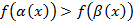4. Сформулировать условие задачи, усложнив в необходимой мере уравнение (неравенство): 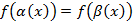(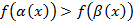), распределив некоторые слагаемые по разным частям и спрятав тем самым общий вид исходной функции .
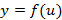5. Решить для проверки полученную задачу, применив ранее сформулированный алгоритм.
Затем мы предлагаем студентам реализовать представленный алгоритм с заданными функциями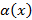 
, 
, 
.
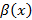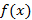Возникает вопрос, как подобрать монотонную функцию 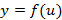? Для этого можно воспользоваться элементарными монотонными функциями, можно на основе свойств суммы, разности и произведения монотонных функций строить новые.
При изучении данной темы студентами были составлены разноуровневые задачи, решаемые данным методом:
1-й уровень.
1. 
.
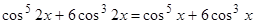2. 
.
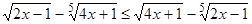3. 
.
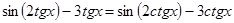В этих уравнениях и неравенствах легко определяются функции , ,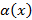 
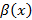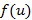. Монотонность функции 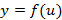из свойств монотонных и элементарных функций.
2-й уровень.
1. 
.
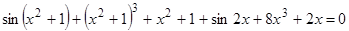2. 
.
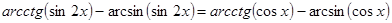3. 
.
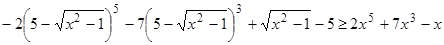Сложность в подборе функции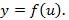 
Существенные ограничения на область определения функции 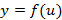, а значит, на значения функций 
и .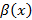
3-й уровень.
1. 
.
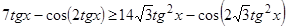2. 
.
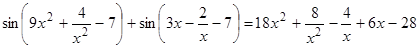3. 
.
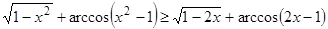На этом уровне присутствует существенная сложность в подборе функции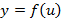 
, в доказательстве ее монотонности, существенные ограничения на область определения функции 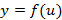, а значит, на значения функций и .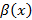
Формированию компетенций, способствующих выработке навыков составления задач, необходимо уделять постоянное внимание. Так, при изучении темы «Область значения функции» делается акцент на различного рода ограниченности функций.
После изучения соответствующего приема решения студентам было дано задание составить и решить задачи, в решении которых можно использовать данную теорему. Студенты предложили следующие задания:
1. 
.
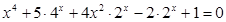2. 
.
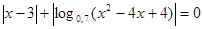3. 
.
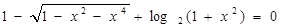Сами же студенты расширили рамки изучаемого метода и предложили следующее утверждение уже для неравенств:
Пусть левая часть неравенства
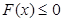
может быть представлена в виде суммы функций (2), каждая из которых неотрицательна на области допустимых значений неравенства, тогда справедлива следующая равносильность:
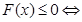
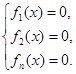
Студентами были составлены следующие задачи:
1. 
.
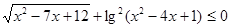2. 
.
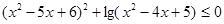3. 
.
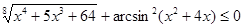4. 
.
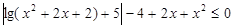Приемы составления задач и формулировки новых утверждений настолько увлекли студентов, что они фактически самостоятельно пришли к формулировке следующих утверждений:
1. Если требуется решить уравнение (неравенство)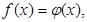 
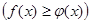
и на области допустимых значений справедливы ограниченности функций: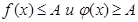 
, то имеют место следующие равносильности:
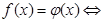
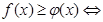
2. Если для уравнения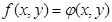 
на области допустимых значений выполняются ограничения на значения функци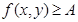й: 
и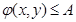 
, то справедлива равносильность
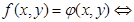
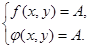
Студентами были составлены следующие задачи, при решении которых могут быть использованы сформулированные утверждения:
1. 
.
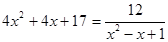2. 
.
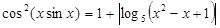3. 
.
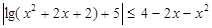4. 
.
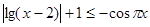5. 
.
Много возможностей для формирования навыков умения составлять задачи дает геометрия. В силу разнообразия геометрического материала, логики строения и решения геометрических задач мы постоянно сталкиваемся с необходимостью отыскания подзадач прямой задачи, их формулировки и решения, с формулировкой прикладных задач с анализом подбора необходимых и достаточных условий рассматриваемой ситуации [8-10]. Большие возможности дает геометрия для формулировки новых задач при решении задач на построение, особенно на этапе анализа уже решенной задачи. Так, исходя из проведенного анализа задачи на построение, можно формулировать задачи с заданными свойствами решений. В статье мы рассмотрим прием открытых задач. Студентам формулируется условие задачи, они же должны сформулировать вопрос и решить ее.
Студентам было предложено следующее условие: «Даны три отрезка, длины которых относятся как 3:4:5. Постройте треугольник так, чтобы…». Студентами составлены и решены были следующие задачи:
А. Эти отрезки были его сторонами и медианой, выходящими из одной вершины.
Б. Два из этих отрезков были медианой и стороной, выходящими из одной вершины, а третья – стороной, к которой проведена медиана.
В. Эти отрезки были его сторонами и высотой, выходящими из одной вершины.
Г. Два из этих отрезков были высотой и стороной, выходящими из одной вершины, а третья – стороной, к которой проведена высота.
Рассмотрите все возможные случаи. Сколько решений имеет задача при каждом наборе элементов?
Заключение. Именно содержание математического образования в школе требует от учителей знания приемов составления задач, а также дает возможность формулировки большого и разнообразного круга задач, которые могут составить сами учителя, в зависимости от целей, реализуемых на данном этапе обучения. Компетенции, позволяющие сформировать навыки составления задач, не должны оставаться за рамками нашего внимания при обучении будущих учителей.