Умение решать задачи – один из главных показателей уровня математической подготовки учащихся и глубины усвоения ими учебного материала. Важнейшей целью обучения математике в общеобразовательной школе является овладение учащимися методами решения определенных типов математических задач.
Одним из самых сложных разделов математики в школе является решение стереометрических задач, т.к. они требуют и развитого пространственного воображения, навыка проводить непростые алгебраические преобразования, а также умения выбирать способ решения [1; 2].
Реализация дидактического принципа вариативности предполагает развитие у учащихся вариативного мышления, т.е. формирование способностей к систематическому перебору вариантов и адекватному принятию решений в ситуациях выбора.
Особое место в стереометрии занимают задачи на поиск экстремальных значений. В общем виде одну из задач этого типа можно сформулировать следующим образом: найти минимальную площадь сечения треугольной пирамиды плоскостью, проходящей через ее заданное ребро и пересекающей противоположное.
Цель исследования
Разработка методики формирования у школьников стремления к выбору метода решения на примере стереометрических задач на поиск экстремальных значений.
Материал и методы исследования
Задача. Основанием треугольной пирамиды ТАВС является равносторонний треугольник АВС со стороной основания, равной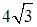 
. Высота пирамиды совпадает с боковым ребром ТА и равна 
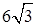. Какую наименьшую площадь S может иметь сечение пирамиды плоскостью, проходящей через сторону основания АС и пересекающей боковое ребро 
?
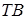В настоящей статье мы рассмотрим три метода решения задачи: геометрический [3], [4], алгебраический с использованием производной [5-7], а также метод использованием векторной алгебры (для учащихся школ с углубленным изучением математики) [8-10].
Результаты исследования и их обсуждение
Первый метод решения.
Пусть плоскость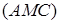 
– искомое сечение (рис. 1).
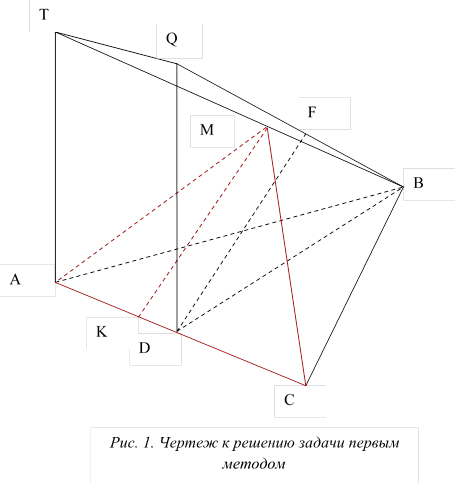
Проведем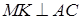 
, тогда искомая площадь вычисляется по формуле 
.
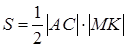Поскольку длина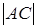 
фиксирована, то значение площади S будет минимальным тогда и только тогда, когда длина отрезка 
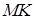минимальна. В свою очередь, длина отрезка 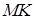минимальна тогда и только тогда, когда 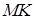является расстоянием между скрещивающимися прямыми и 
.
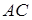Таким образом, задача свелась к нахождению расстояния между двумя скрещивающимися прямыми. Отметим, что данный способ не требует нахождения местоположения точки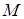 
на ребре .
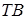Найдем расстояние между скрещивающимися прямым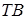и и .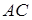
Проведем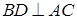 
, тогда 
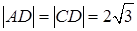, (т.к. 
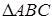– равносторонний, высота в нем совпадает с медианой и биссектрисой).
Проведем DQ║AT,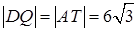 
.
Тогда TQ║AT,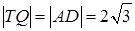 
.
Обозначим за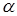 
плоскость 
.
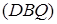Так как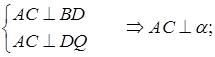 
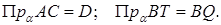
Проведем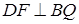 
. Так как 
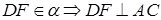, т.е. 
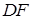и является расстоянием между скрещивающимися прямым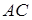и и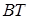 
.
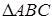– равносторонний, следовательно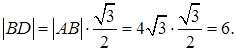 
По теореме Пифагора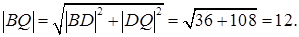 
Т.к.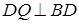 
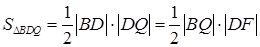, откуда
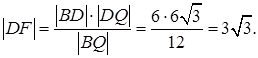
Тогда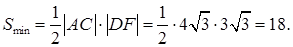 
В общем виде алгоритм решения задач данного типа первым методом можно представить таким образом:
1) записывается формула для вычисления площади сечения в общем виде;
2) выясняется, что минимальная площадь сечения достигается в случае, если длина высоты полученного в сечении треугольника является расстоянием между определенными скрещивающимися прямыми;
3) находится это расстояние;
4) находится минимальная площадь сечения.
Второй метод решения.
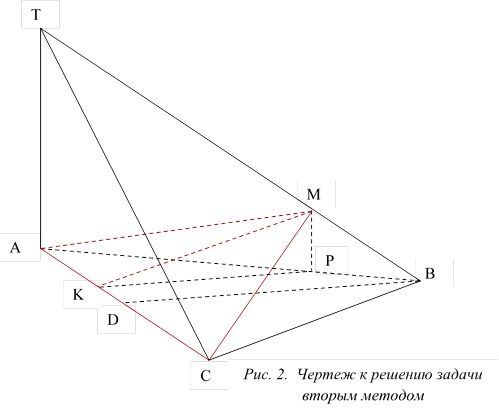
Пусть плоскость – искомое сечение (рис. 2).
Проведем 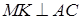, тогда искомая площадь вычисляется по формуле .
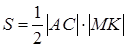Проведем МР║ТА ⇒ МР ⊥ (АВС) ⇒ МР ⊥ АВ.
Проведем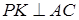 
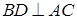,, тогда , 
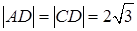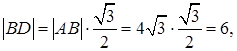т.к. 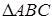– равносторонний.
Обозначим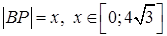 
, тогда 
.
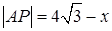Из подобия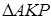 
и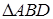 
получаем:
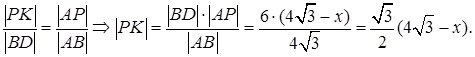
Из подобия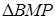 
и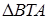 
получаем:
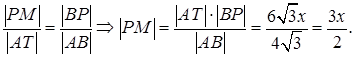
По теореме Пифагора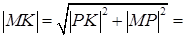 
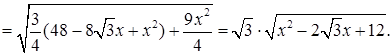
Тогда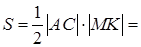 
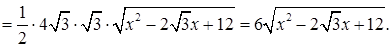
Поскольку величина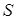 
не может быть отрицательной, то 
.
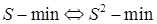Обозначим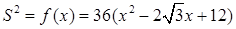 
.
Найдем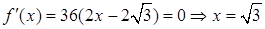 
.
Убедимся, что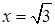 
является точкой минимума функции 
.
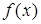Для этого найдем знаки производной функции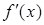 
на интервалах 
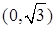и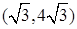 
(рис. 3).
Таким образом, 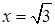является точкой минимума функции 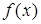. Поэтому 
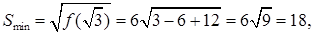т.е.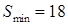 
.
В общем виде алгоритм решения задач данного типа вторым методом можно представить таким образом:
1) вводится неизвестная величина – расстояние от точки пересечения искомого сечения с соответствующим ребром пирамиды до одной из его вершин;
2) составляется функция для вычисления площади искомого сечения, зависящая от введенной неизвестной величины;
3) вычисляется производная этой функции и проверяется, что при значении производной, равной нулю, данная функция достигает своего минимума;
4) для вычисления площади сечения в функцию подставляется найденное значение неизвестной величины и вычисляется минимальное значение площади сечения.
Третий метод решения.
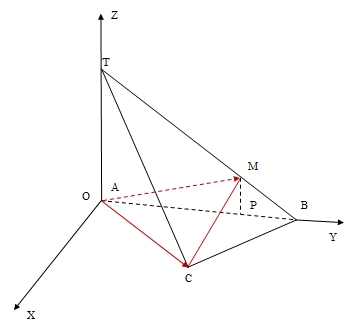
Рис. 4. Чертеж к решению задачи третьим методом
Введем в трехмерном пространстве правую декартову систему координат. Начало координат совпадает с точкой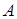 
, ось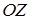 
совместим с высотой 
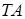, ось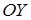 
– c ребром основания 
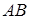, ось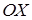 
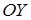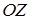проведем перпендикулярно осям и . Ось 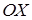будет лежать в плоскости основания пирамиды (рис. 4).
Пусть плоскость 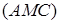– искомое сечение. Тогда искомая площадь вычисляется по формуле 
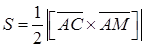(половина длины векторного произведения векторов 
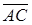и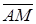 
. Найдем координаты этих векторов.
Проведем MP¦TA. Обозначим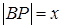 
, тогда .
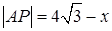Из подобия 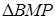и 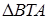получаем:
,
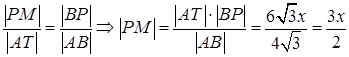а вектор 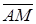имеет координаты 
.
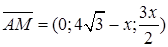Так как – равносторонний, 
, координаты вектора следующие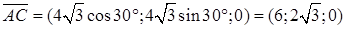 
.
Найдем векторное произведение векторов 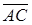и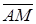
.
Вычисляем его длину
,
.
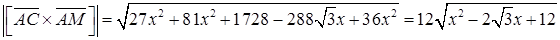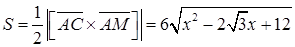Далее проводим такие же действия, как и в предыдущем способе, и получаем, что .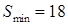
В общем виде алгоритм решения задач данного типа третьим методом можно представить таким образом:
1) вводится декартова система координат в трехмерном пространстве;
2) вводится неизвестная величина и через нее записываются координаты всех точек, используемых при решении задачи;
3) используя векторное произведение двух векторов, составляется функция для нахождения площади искомого сечения, зависящая от введенной неизвестной.
Далее выполняются пункты 3), 4) второго метода.
Таким образом, третий метод решения поставленной задачи является комбинацией методов векторной алгебры и математического анализа.
Заключение
Отметим, что представленные методы решения стереометрических задач на нахождение экстремальных значений достаточно близки по трудоемкости. Учащиеся, обладающие хорошо развитым пространственным воображением, выбирают, как правило, первый способ решения. Второй способ часто предпочитают учащиеся, хорошо освоившие алгебру и основы математического анализа. Учащиеся школ с углубленным изучением математики, знакомые с основами векторной алгебры, предпочитают третий способ.
Поэтому целесообразно ознакомить школьников с различными методами решения задач данного типа и оставить выбор способа решения на их усмотрение.