В условиях модернизации отечественного высшего образования становится актуальной проблема развития самообразования обучающихся. Порождается она информатизацией современного общества, необходимостью усваивать обучающимися постоянно увеличивающийся периодически обновляющийся поток научной информации, новые методы, технологии использования полученных знаний и способов деятельности на практике, перестройкой образовательного процесса в сторону увеличения доли самостоятельной работы, меняющимися потребностями общества в специалистах-педагогах различных профилей. Все это говорит о том, что выпускник педвуза должен уметь проанализировать и оценить имеющийся у него запас профессиональных знаний и способов деятельности, их соответствие требованиям времени, наметить траекторию профессионального роста или переквалификации. Следовательно, уже в период обучения в вузе будущий учитель должен овладеть умениями анализировать и оценивать качество усвоения предметных, педагогических, методических знаний и способов деятельности, вырабатывать потребности в их пополнении и обновлении. Соответствующие требования к выпускникам вузов находят отражение в нормативно-правовой документации, регламентирующей подготовку специалистов для сферы педагогического образования (профиль «Математика») [1], развитие российского непрерывного образования [2], и в исследованиях педагогов-исследователей: Э.Ф. Зеера, И.А. Зимней, И.Ф. Медведева [3, 4, 5].
Процесс развития понятия «самообразование» нашел отражение в работах Ю.В. Сенько, Л.Г. Титовой, В.В. Юдина [6], И.Ф. Медведева [5], в которых оно обрело современные характеристики. В контексте настоящего исследования представляют интерес: опыт формирования индивидуальных траекторий обучения [3], опыт организации пролонгированного оценивания учебной деятельности студентов, основанного на регулярном мониторинге поступательного продвижения по пути усвоения учебного материала, формирования умений самооценивания обучающимися своей деятельности путем вовлечения их в процесс выработки критериев оценки результатов [7]. Исследования В.И. Загвязинского [8], А.В. Хуторского [9, 10], авторский опыт внедрения новшеств в образовательный процесс указывают на необходимость сопровождать инновации дидактическим инструментарием, способствующим комплексной реализации всех аспектов новшества. Итак, краткий анализ литературы по теме исследования свидетельствует о недостаточной разработанности системного подхода к созданию дидактического сопровождения развития самообразования, а именно с позиций взаимосвязи поставленной цели, выявляемой структуры, наполнения содержанием каждого компонента и конечного результата.
Целями настоящей статьи являются теоретическое обоснование и конструирование дидактического обеспечения развития самообразовательной деятельности будущего учителя, включая наполнение содержанием каждого структурного компонента.
Материал и методы исследования. Теоретической основой настоящего исследования являются: основные положения системного и деятельностного подходов в образовании, разработанные И.А. Зимней [4], А.В. Хуторским [10] и иными; ведущие положения концепции самообразования, изложенные в работах И.Ф. Медведева [5], основные положения изысканий В.И. Загвязинского [8], А.В. Хуторского [9] в области методологии научного исследования и внедрения новшеств в образовательный процесс, результаты исследований в области развития профессиональной рефлексии П.Н. Осипова [11], Л.А. Одинцовой, Л.М. Бронниковой [12]. В исследовании использованы методы: анализа, синтеза, абстрагирования, конкретизации, обобщения и систематизации авторского опыта, педагогического эксперимента.
Результаты исследования и их обсуждение. Раскроем понятийный аппарат исследования. На основе анализа развития понятия самообразования за основу в настоящем исследовании примем трактовку, сформулированную в работе И.Ф. Медведева [5]. Под самообразованием будем понимать систематическую целенаправленную исследовательски ориентированную познавательную деятельность, направленную на достижение определенных личностных или социально значимых образовательных целей, управляемую самой личностью. С опорой на работы И.Ф. Медведева выделим следующие его признаки: 1) развитая внутренняя мотивация; 2) самостоятельность в деятельности и мышлении, самоактуализация, развивающие непрерывность самообразования; 3) самореализация и саморазвитие; 4) механизмы самоуправления: системность и систематический характер этой деятельности, самонаблюдение и рефлексия, планирование (самоорганизация и самопознание), осуществление (самообучение), самоконтроль и самооценка.
Итак, обучаясь в педвузе, студент готовит себя к профессиональной деятельности, осуществлять которую будет самостоятельно. К тому же он должен будет сам заботиться о пополнении знаний и способов деятельности в предметной области, педагогике и методике преподавания. Он должен сам уметь ставить образовательные цели и научить этому своих учеников, подобрать систему заданий, методов и технологий для организации образовательной деятельности обучающихся, осуществить контроль за ходом деятельности и полученными результатами. Будущий учитель будет сам организатором образовательного процесса, поэтому должен овладеть всем арсеналом средств его профессионального управления. Задача вузовского преподавателя – помочь ему в этом. Для оперативного управления образовательным процессом, ориентированным на развитие самообразовательной деятельности будущего учителя, у преподавателя-предметника должен быть подготовлен запас дидактических средств управления каждым из этапов образовательного процесса, имеющим свое функциональное назначение. Выясним, каким должно быть дидактическое обеспечение образовательного процесса, ориентированного на развитие самообразовательной деятельности будущего учителя, каковы его структура, составляющие, содержание составляющих. Исходя из признаков самообразовательной деятельности конструирование дидактического обеспечения развития самообразовательной деятельности будущего учителя начнем с выделения принципов, которым оно должно удовлетворять. Поскольку конструируемый объект имеет определенную цель – формирование самообразовательной деятельности, то все его компоненты должны подчиняться этой цели, быть взаимосвязаны и носить деятельностный характер. Следовательно, в качестве основных следует выбрать принципы системности и деятельности. Непосредственно из признаков самообразования вытекают следующие два принципа – рефлексии и управляемости. Еще одним важным принципом является принцип взаимодополняемости контактной и внеконтактной самостоятельной работы обучающихся. Контактная самостоятельная работа, выполняемая под непосредственным управлением преподавателя, служит образцом для организации и выполнения внеконтактной работы.
Приступим к описанию конструирования дидактического обеспечения развития самообразовательной деятельности будущего учителя.
Компонентом 1 дидактического обеспечения выступает генеральная цель – развитие самообразовательной деятельности будущего учителя-предметника. Ей должно быть подчинено функционирование всех остальных компонентов создаваемого объекта. Учитывая специфику самообразования, считаем целесообразным выделить следующие компоненты его дидактического обеспечения: 2) банк заданий для самообразовательной деятельности; 3) электронный курс дисциплины, включающий: а) курс лекций; б) содержание практических занятий; в) задания для контактной самостоятельной работы; 4) задания для внеконтактной самостоятельной работы; памятки, указания, рекомендации; 5) фонд контрольных средств по дисциплине; 6) критериальный аппарат оценивания контрольных срезов.
Схематически его структура представлена на рисунке.
Структура дидактического обеспечения развития самообразовательной деятельности будущего учителя
Компонент 2. Банк заданий для самообразовательной деятельности представляет систему учебных заданий, служащих средством организации самостоятельной деятельности студентов, направленной на усвоение научных знаний по предмету, знаний о видах профессиональной деятельности (включая самообразовательную) и овладение приемами их использования на практике, что будет обеспечивать приобретение и развитие профессионального опыта. Эта система структурируется по разделам и темам курса. Подсистема каждого раздела должна содержать следующие группы заданий.
I. Задачи на осознание сущности общенаучных методов познания, логических методов построения рассуждений и развитие умений и навыков их применения при усвоении математических знаний и способов деятельности. Для развития самообразовательной деятельности будущего учителя важно проиллюстрировать и научить применять общенаучные методы при формировании новых математических понятий (выделение сущностных характеристик, объема понятия). Приведем некоторые конкретные примеры.
1. Выделите объем и содержание понятия «стационарная точка». Как изменится объем понятия, если сократить или дополнить его содержание?
2. Проведите сравнительный анализ понятий: «точка экстремума», «точка максимума», «точка минимума», «максимум функции», «минимум функции», «стационарная точка», «критическая точка», «точка разрыва функции», «точка перегиба», «точка излома». Изобразите на кругах Эйлера соотношение объемов этих понятий.
3. Выделите свойства, которыми не обладает понятие «нечетная функция»: а) каждому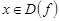 
соответствует единственный
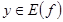; б) область определения симметрична относительно начала координат; в) график симметричен относительно оси ординат; г) график симметричен относительно начала координат; д) для любого 
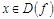выполняется 
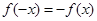, е) существует 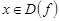, для которого выполняется 
.
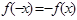II. Задачи, способствующие развитию умений и навыков самостоятельно добывать знания, вычленять проблемы, вести поиск приемов их решения, критически осмысливать новые знания, умения и способы решения, выявлять наиболее рациональные. Для достижения указанных целей наиболее подходят задания, побуждающие студентов делать для себя учебные математические открытия (факты и методы, известные в науке, но являющиеся новыми для обучающихся), актуализирующие необходимость применения знаний в новой ситуации, носящие опережающий и открытый характер.
Примерами могут послужить ниже следующие задания.
1. Докажите: а) прямоугольным треугольником максимальной площади с заданной суммой катетов является равнобедренный треугольник; б) прямоугольник наибольшей площади, вписанный в круг, является квадратом; в) из всех прямоугольных треугольников с заданной гипотенузой наибольшую площадь имеет равнобедренный треугольник.
2. Докажите: из всех плоских фигур равного периметра наибольшую площадь имеет круг. Опираясь на данное утверждение, вставьте пропущенное слово в предложение «Из всех плоских фигур равной площади … периметр имеет круг», чтобы получилось верное утверждение, и докажите его.
III. Задачи творческого характера, выполнение которых предполагает деятельность студентов: выбор задач из некоторой совокупности решаемых некоторым заданным методом или комбинацией методов, сравнение полученных решений, выбор наиболее рационального; решение задач с избыточным несформированным, противоречивым условием; составление новых задач (обратной, противоположной, аналогичной и др.), подготовка рецензий, проектов, кейсов, портфолио. Конкретизируем задания данной группы.
1. Каковы должны быть стороны прямоугольника, согнутого из проволоки, чтобы его площадь получилась наибольшей? (у студента нет возможности приступить к решению без знания длины имеющейся проволоки).
2. Задание на выбор студента: а) имея целью продемонстрировать приложения производной, подготовьте сборник задач из дополнительных источников; б) выберите одну из областей приложения производной (физика, химия, экономика, техника и т.д.) и с помощью презентаций продемонстрируйте возможности производной.
3. Найдите наибольшее значение функции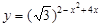 
одним из трех способов, выбрав наиболее рациональный: а) с помощью производной функции; б) используя монотонность функции; в) методом оценки.
IV. Задачи прикладной направленности, предполагающие развитие мотивации к самообразовательной деятельности, стимулирующие повышение интереса к математике, раскрывающие ценность и мощь математического языка и методов исследования в различных областях знания и практической деятельности. Проиллюстрируем примерами.
1. Вокруг прямоугольного поля площадью 400 га надо посадить со всех сторон деревья в форме полосы шириной 10 м. Каковы должны быть линейные размеры поля, чтобы площадь, занимаемая деревьями, была наименьшей?
2. Канат висячего моста имеет вид параболы и прикреплен к вертикальным опорам, отстоящим одна от другой на 200 м. Самая нижняя точка каната находится на 40 м ниже точек подвеса. Найдите угол между канатом и опорными колоннами.
V. Задачи на формирование рефлексивной составляющей самообразовательной деятельности. Их главное назначение – развитие креативности, инициативности, целеустремленности, способности к самоанализу, к предвидению и прогнозированию результатов своей самообразовательной деятельности. Приведем примеры вопросов рефлексивного характера к задачам, задаваемых после решения: Какие затруднения возникали при выполнении задания? Правильно ли Вы спланировали свою деятельность? Какие ошибки были допущены? Что необходимо предпринять, чтобы не допускать такие ошибки? Какая помощь требуется для этого?
VI. Для формирования самоуправленческих умений и навыков в систему целесообразно включать задания на: 1) анализ фактической ситуации, включающий определение уровня сформированности знаний и способов деятельности для работы над фрагментом учебного материала; 2) планирование деятельности, предполагающее разработку последовательности действий для достижения поставленной цели; 3) организацию деятельности, т.е. выполнения спланированной последовательности действий в системе самостоятельной работы студентов; 4) осуществление самоконтроля за выполнением последовательности действий; 5) организацию коррекционной работы (повторение теоретических основ выполнения заданий, исправление ошибок).
Компонент 3. Электронный курс по дисциплине включает: 1) электронный курс лекций, спецификой которого является расширенный объем примеров, конкретизирующих вводимые понятия, разъяснений рассматриваемых теорем и их доказательств, примеров использования изучаемого теоретического материала на практике; 2) планы практических занятий; 3) задания для контактной самостоятельной работы с рекомендациями использования для организации учебной деятельности методов, средств, технологий.
Компонент 4. Задания для внеконтактной самостоятельной работы. Эта система заданий, взятая из Банка заданий (Компонент 2), структурированная по разделам и темам, предназначена для организации самостоятельной работы, выполняемой во внеаудиторное время без непосредственного контакта с преподавателем. Поэтому она снабжена необходимыми памятками, указаниями, рекомендациями.
Компонент 5. Фонд контрольных средств по дисциплине содержит: 1) перечень всех контрольных срезов по предмету (контрольные работы; индивидуальные, творческо-поисковые, проектные задания, зачетные задания, перечень вопросов к экзамену); образцы каждого вида задания для ознакомления студентов; 2) комплекты заданий различных видов для организации контроля преподавателями. Если дисциплина изучается несколько семестров, данный фонд содержит комплекты таких заданий для каждого семестра.
Компонент 6. Критериальный аппарат оценивания контрольных срезов содержит перечень критериев сформированности самообразовательной деятельности и конкретизирующих показателей: 1) мотивационный (целеустремленность); 2) когнитивный (знание и понимание понятий, фактов, приемов и способов деятельности в предметной и методической областях); 3) деятельностный (умение и владение приемами и способами деятельности в предметной и методической областях). Все показатели конкретизируются для каждой темы или раздела, по которым осуществляется контроль. Для отслеживания динамики сформированности самообразовательной деятельности выделены три уровня (даны их характеристики при помощи выделенных показателей).
Созданное дидактическое обеспечение развития самообразовательной деятельности будущего учителя прошло опытно-экспериментальную проверку в течение года в рамках одного вуза в преподавании математического анализа на первом курсе. Первая часть эксперимента была посвящена использованию электронного дидактического инструментария для организации в условиях очного обучения контроля, взаимоконтроля, самоконтроля и коррекции самообразовательной деятельности студентов, вторая – для организации дистанционного образовательного процесса, ориентированного на развитие самообразовательной деятельности: установление обратной связи, своевременное оказание необходимой помощи студентам. Проведенный на основе разработанного критериального аппарата сравнительный анализ (с использованием математических методов) результатов входного и итогового контроля (соответственно в начале и конце учебного года) показал положительные сдвиги в развитии самообразовательной деятельности.
Выводы. В настоящем исследовании теоретически обоснованы и разработаны структура и содержание дидактического обеспечения развития самообразовательной деятельности. Проведенная опытно-экспериментальная проверка его функционирования позволяет сделать следующие заключения.
1. Реализация построенного дидактического обеспечения развития самообразовательной деятельности будущего учителя способствует формированию мотивации, о чем свидетельствует достаточно быстрое появление нацеленности на деятельность, на освоение нового, чувства ответственности за своевременность и качество выполнения заданий, соответствие предъявляемым требованиям.
2. Предлагаемый электронный курс дисциплины в значительной мере гармонизирует теоретическую и практическую составляющие подготовки учителя математики: курс лекций способствует осознанному усвоению сути изучаемых математических фактов и способов деятельности, практические занятия нацеливают внимание обучающихся на факты, служащие основой выполнения определенных способов деятельности, что в совокупности с использованием рефлексивных заданий способствует выработке умений аргументировать свои утверждения, правильно выбирать методы решения учебных проблем.
3. Задания для внеконтактной самостоятельной работы и фонд контрольных средств служат инструментом оперативной организации самообразовательной деятельности; критериальный аппарат – средством ориентации в предъявляемых требованиях к выполнению самообразовательной деятельности.
4. Выявленная положительная динамика сформированности самообразовательной деятельности студентов свидетельствует об эффективности разработанного дидактического обеспечения ее развития.