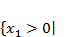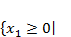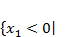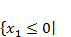Ежегодно в письменной части профильного единого государственного экзамена по математике выпускникам предлагается решить задачу с параметрами (задание 18) [1]. Это задание относится к высокому уровню сложности, оценивается в четыре первичных балла (максимальный балл из возможных). Согласно опубликованным данным анализа результатов ЕГЭ [2; 3], за последние пять лет видна растущая заинтересованность учащихся в правильном выполнении задания с параметрами.

Проведенный анализ школьных учебников и задачников по алгебре и началам анализа позволяет сделать следующие выводы.

В задачниках Мордковича А.Г. [4-5] и Виленкина Н.Я. [6] представлен достаточно большой объем упражнений, требующих умения применять различные методы решений заданий с параметрами. В учебнике Алимова Ш.А. [7] материал по методам решения задач с параметрами представлен незначительно. В основном рассматривается аналитический способ решения.

В учебнике Колмогорова А.Н. [8] задачи с параметрами включены в раздел «Повторение. Задачи повышенной трудности». Разобранных примеров, иллюстрирующих методы решения задач с параметрами, не приводится.

Наиболее большой спектр заданий с параметрами представлен в сборнике задач Галицкого М.Л. [9]. В нем содержатся уравнения и неравенства, системы уравнений и неравенств первого и второго порядка с параметрами, для решения которых можно применять аналитический и (или) графический методы решения. Задания располагаются в порядке повышения сложности.

В школьных учебниках практически отсутствуют объяснения решений задач с параметрами. Существует множество пособий по решению таких задач [10-13]. Заметим, что они в основном ориентированы на хорошо подготовленных учащихся, тогда как в школьных программах по математике задачам с параметрами отводится небольшое количество времени, рассматривается небольшой круг заданий.

Умение решать задачи с параметрами является одним из важнейших показателей уровня математической подготовки и глубины освоения материала. В школьной программе 8–11 классов задачи с параметрами обычно рассматриваются в конце каждой темы, что позволяет учащимся обобщать и структурировать полученные знания. Решение задач с параметрами развивает способность анализировать и формирует навыки логического мышления.

Нужно отметить, что задачи, содержащие параметр, очень разнообразны, и при их решении используются различные методы (графический, аналитический, перебор вариантов, комбинированный и т.д.). Наибольшую трудность для учащихся как раз составляет выбор «правильного» метода, позволяющего обоснованно и с наименьшими затратами выполнить решение задачи.

Цель исследования: показать необходимость изучения школьниками метода, основанного на применении теоремы Виета, для решения систем уравнений с параметрами, сводящихся к квадратному уравнению. При этом на область допустимых значений переменной (ОДЗ) накладывается определенное условие, определяемое из условия задачи.

Материал и методы исследования. Рассмотрим следующую задачу. Дана система уравнений, которая сводится к квадратному уравнению вида

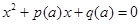, (1)

содержащему параметр 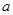. При этом, исходя из условий задачи, область допустимых значений (ОДЗ) для неизвестной переменной 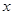имеет вид 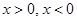(2)

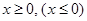либо (3).

Дискриминант уравнения равен 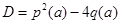. Обозначим 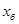и 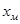соответственно больший и меньший корни уравнения (1).

Зачастую учащиеся пытаются непосредственно найти решения уравнения (1) и определить, при каких значениях параметра 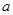на ОДЗ попадает нужное число решений. В этом случае задача сводится к решению иррационального неравенства либо системы иррациональных неравенств.

Если требуется найти значения параметра 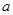, при которых уравнение (1) с ОДЗ (3) имеет два различных решения, получаем:

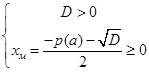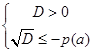или . (4)

Если требуется найти значения параметра 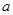, при которых уравнение (1) с ОДЗ (3) имеет единственное решение, приходим к следующей совокупности систем уравнений и неравенств:

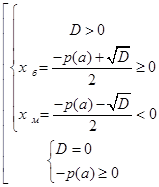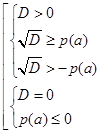или . (5)

Если же для уравнения (1) с ОДЗ (3) требуется найти значения параметра 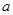, при которых оно имеет хотя бы одно решение, получаем

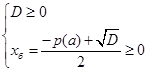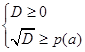или . (6)

В том случае, когда дискриминант уравнения (1) является полным квадратом, решение систем (4), (6) либо совокупности (5) не вызывает у выпускников трудностей. В противном случае само по себе решение иррациональных неравенств – сложная задача, ведь каждое из этих неравенств, в свою очередь, сводится к решению системы неравенств и приводит чаще всего к ряду ошибок.

Для уравнения (1) при ОДЗ 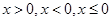получаем аналогичную картину.

В пособиях [10; 12] для решения рассматриваемого класса задач используется графический метод, основанный на исследовании расположения корней квадратного трехчлена относительно нуля. Этот метод больше подходит учащимся с развитым визуальным восприятием.

Использование теоремы Виета подойдет учащимся, склонным к аналитическому мышлению. Предлагаемый метод позволяет, на наш взгляд, существенно упростить решение рассматриваемой задачи, избежав решения иррациональных неравенств.

Пусть дано квадратное уравнение

,

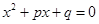его дискриминант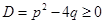, его корни и . Тогда получаем следующие условия (таблица).

Соответствие между корнями квадратного уравнения и его коэффициентами

Естественно, данная таблица не подлежит заучиванию. Учащимся необходимо объяснить механизм приведенных соответствий, следующих из теоремы Виета.

Используя соответствия, представленные в таблице, при решении выше поставленной задачи приходим к системам, не содержащим иррациональных неравенств.

Если требуется найти значения параметра 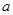, для которых уравнение (1) при ОДЗ (3) имеет два различных решения, приходим к системе

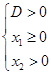или .

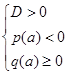Для нахождения значений параметра 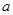, для которых уравнение (1) при ОДЗ (3) имеет единственное решение, получим:

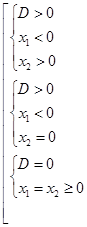или .

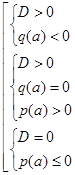Для нахождения значений параметра 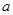, при которых уравнение (1) при ОДЗ (3) имеет хотя бы одно решение, получаем следующую совокупность систем неравенств:

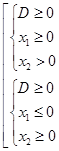или .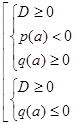

Уравнение (1) при ОДЗ 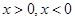или 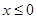исследуется аналогично.

Рассмотрим следующие примеры.

Пример 1. Найти значения параметра 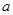, при которых система уравнений

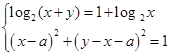(7)

имеет а) два различных решения; б) единственное решение; в) хотя бы одно решение.

Решение. Из первого уравнения получаем

.

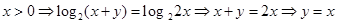Поскольку для каждого значения переменной 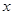значение переменной 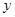находится однозначно, то число решений системы (7) при каждом из значений параметра 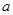соответствует числу решений системы

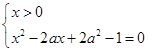. (8)

а) Система (8) имеет два различных решения при

.

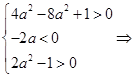
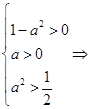
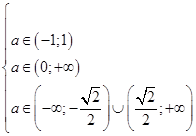Окончательно, .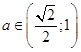

б) Система (8) имеет единственное решение при

.

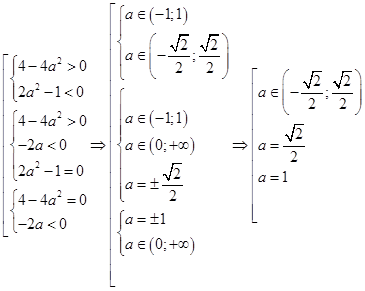Окончательно, .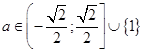

в) Система (8) имеет хотя бы одно решение при

.

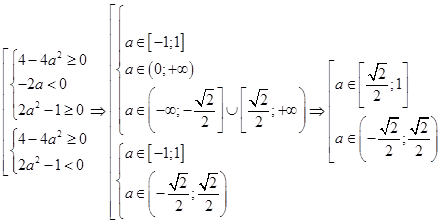Окончательно, .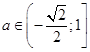

Находя корни квадратного уравнения непосредственно, имеем

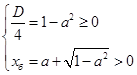
содержащую иррациональное неравенство.

Пример 2. Найти значения параметра 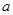, при которых система уравнений

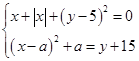(9)

имеет

а) два различных решения; б) единственное решение; в) хотя бы одно решение.

Решение. Поскольку при 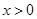первое уравнение системы не имеет решений, то рассматриваем только 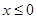. Тогда из первого уравнения системы

.

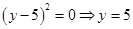
Задача свелась к нахождению числа решений системы

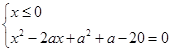(10)

в зависимости от параметра .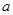

а) Система (10) имеет два различных решения, если

.

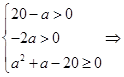
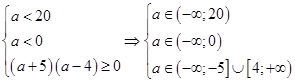Окончательно, .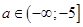

б) Система (10) имеет единственное решение при

.

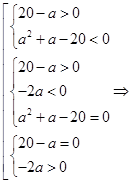
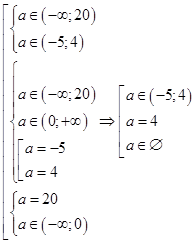Окончательно, .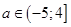

в) Система (10) имеет хотя бы одно решение при

.

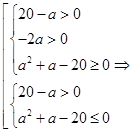
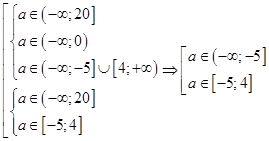Окончательно, .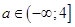

Заключение. Предложенный в статье метод решения задач достаточно легко усваивается учащимися. Навык использования теоремы Виета быстро развивается. Такой способ решения подойдет учащимся, склонным к аналитическому мышлению. Отметим, что важно познакомить выпускников со всеми методами решения задач с параметрами, поскольку зачастую при решении таких задач используется комбинированный подход.

Приведенные примеры иллюстрируют преимущество данного метода по сравнению с непосредственным нахождением корней, дальнейшей проверкой их попадания на ОДЗ и последующим определением значений параметра, удовлетворяющих условию поставленной задачи. При использовании данного метода, в отличие от стандартного метода, отпадает необходимость решения одного или нескольких иррациональных неравенств.