Учитывая это, можно говорить, что система не обладает избыточностью и не является слишком сложной, если ее нельзя упростить, сохранив при этом достаточно высокий уровень ее совершенства. Игнорирование сложности создаваемой системы может приводить к ситуациям, в которых незначительное повышение качества управления достигается неоправданно высоким усложнением системы.
В качестве параметра интегральной оценки избыточности синтезируемых устройств предлагается использовать коэффициент избыточности R [2]. Согласно доказанной Шенноном теоремы
H(X;Y) ≤ H(X) + H(Y), (1)
где H(X), H(Y) - энтропия множеств X и Y; H(X;Y) - энтропия результирующего множества, возникшего при взаимодействии исходных множеств X и Y.
Очевидно, что данное соотношение остается справедливым при переходе от рассмотрения абстрактных математических множеств к множествам элементов конкретных физических систем.
Знак равенства в соотношении (1.1) относится к случаю независимых множеств или не вступающих во взаимодействие физических систем. Для всех остальных случаев на основании (1.1) можно записать
∆IS = H(X) + H(Y) - H(X;Y) > 0, (2)
где ∆IS - приращение структурной информации, характеризующей количество новых связей между элементами систем X и Y, возникающих в процессе их взаимодействий.
Частным, но и наиболее характерным, является случай взаимодействия системы Х с окружающей средой Y, при этом происходит процесс адаптации системы к внешним условиям. Образование корреляционных связей между воздействиями среды и реакциями системы приводит к уменьшению энтропии по сравнению максимальной. Данное уменьшение энтропии можно рассматривать как приращение структурной информации, характеризующей упорядоченность (неизбыточность) структуры т.е.
∆IS = HMAX - HR, (3)
где HMAX - максимальная энтропия системы; HR - реальная энтропия.
Таким образом, в результате взаимодействия двух систем или системы с окружающей средой происходит упорядочивание структуры, характеризующееся уменьшением избыточности и наращиваем структурной информации на величину.
Анализ содержательного смысла рассмотренных аналитических соотношений показывает, что величина ∆IS квалифицируется теорией информации как количество избыточной информации, однако ее можно использовать и для оценки структурной упорядоченности системы. Введение понятия потенциального коэффициента полезного действия системы, показывающего, какая часть структурной информации может реализовать требуемый функционал системы, позволяет считать
R = ∆IS / HMAX или R = 1 - HR / HMAX. (4)
Тогда аналогично
R = ∆N / NMAX или R = 1 - NR / NMAX, (5)
где NMAX - максимальное число элементов системы; NR - число элементов системы, способных реализовать все требуемые функции и режимы работы устройства; ∆N - число элементов системы, которое можно исключить без нарушения условий допустимости.
Из рассмотрения соотношений (1.5) следует, что возможно два предельных структурных состояния системы:
- случай при R=1 соответствует жестко детерминированной системе, не способной адаптироваться к изменениям внешней среды. Нормальное функционирование данной системы возможно только в условиях стабильной среды.
- случай при R=0 соответствует системе полностью лишенной структуры, что представляет собой теоретическую абстракцию.
Реальные системы, находясь в промежуточном состоянии, соответствуют условию 1 < R < 0. При этом возникает противоречие, в котором значение R системы, с одной стороны, должно выполнять условиям вариабельности внешней среды, а с другой стороны, не приводить к излишней перегруженности (избыточности) системы. Данное противоречие можно отнести к классу диалектических противоречий, которое разрешается путем формирования и развития иерархических систем.
Процедура микроэлектронного синтеза СФ блоков для систем управления предполагает наличие трех иерархических уровней: структурного, функционального и схемотехнического. При этом информационная емкость системы возрастает в Кi раз по мере перехода с одного уровня иерархии на более высокий структурный уровень. Указанную закономерность для микроэлектронных систем можно представить в виде вписанной в опрокинутый конус спирали, у которой диаметр и длина витка каждого следующего иерархического уровня возрастают в Кi раз (рисунок 1).
При этом коэффициент К показывает соотношение числа элементов системы между различными уровнями. Движение по окружности соответствующего уровня иерархии от точки А, характеризующейся значением коэффициента избыточности R=0 и максимальным количеством элементов системы, к точке В, характеризующейся значением коэффициента R=1, сопровождается снижением избыточности синтезируемого ТО. Наличие дополнительных уровней иерархии, следующих за схемотехническим уровнем, вполне допустимо и может быть связано с исключением избыточности на уровне топологии элементов схемы, процесса изготовления и т.д.
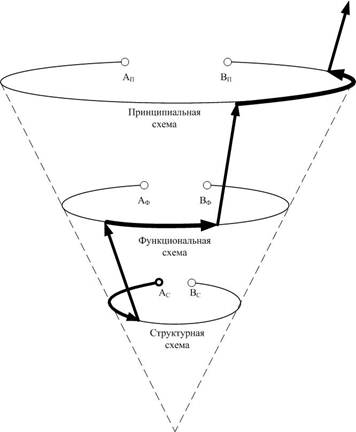
Рисунок 1. Иерархическая модель информационной емкости системы
В реальных системах значение R=1 нереализуемо, так как в этом случае число элементов системы должно быть равно нулю. Максимальное значение R ограничивается предельной величиной RLIM, являющейся оптимальной как с точки зрения адаптивности системы, так и с позиции громоздкости системы. На рисунке 2 представлена зависимость, характеризующая изменение коэффициента R при прохождении поэтапных процедур исключения избыточности.
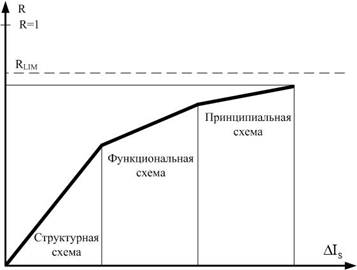
Рисунок 2. Зависимость коэффициента R при иерархическом исключении избыточности
Данная зависимость показывает, что наличие процедур исключения избыточности на всех этапах синтеза СФ блоков позволяет приблизиться к предельному значению RLIM на наименьшее расстояние.
Процесс исключения структурной и функциональной избыточности микроэлектронных сложных функциональных блоков подробно изложен в работах [3,4,5]. Задача исключения избыточности микроэлектронных систем на схемотехническом этапе синтеза рассмотрена в работе [6]. Остановимся более подробно на этапе синтеза схемотехнически интегрированных решений.
Синтез интегрированной принципиальной схемы предлагается осуществлять в соответствии с граф-схемой, представленной на рисунке 3.
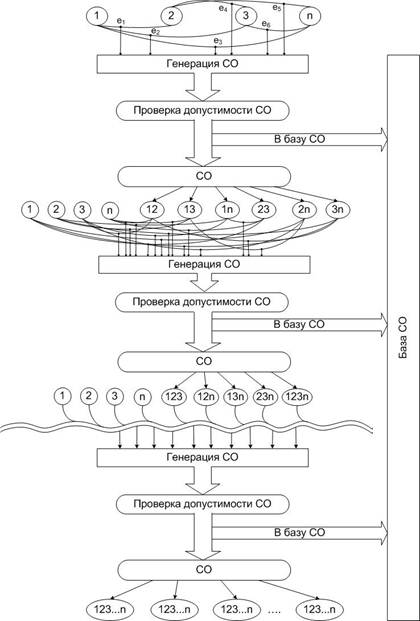
Рисунок 3. Граф-схема процесса синтеза интегрированных схемотехнических решений
В предлагаемом графе в качестве вершин (обозначенных окружностью с номером) используются схемные объекты (СО) из начального набора, соответствующего набору функций принципиальной схемы прототипа. Дуги задают операции схемотехнической интеграции объектов, расположенных в вершинах графа. Таким образом, образуется граф
G = (V,E), (6)
где V = {1,2,3 ... n}, E = {e1, e2, e3, e4, e5, e6,}, e1 = (1,2), e2 = (1,3), e3 = (1,n), e4 = (2,3), e5 = (2,n), e6 = (3,n).
В результате выполнения операции «Генерация СО» формируется дополнительное множество, состоящее из СО, реализуемых путем схемотехнической интеграции исходных СО. Обозначение таких СО и соответствующих им вершин графа состоит из двух номеров СО прототипа, задействованных в получении соответствующего нового СО.
Проверка допустимости сгенерированных схемотехнических решений осуществляется в соответствии с правилами, изложенными в [6]. Допустимые решения заносятся в базу СО.
Во втором этапе схемотехнической интеграции участвуют СО прототипа, а также СО, сгенерированные в первом этапе. При этом результатом генерации являются СО, имеющие в обозначении трехзначный номер. Аналогично первому этапу проводятся операции проверки допустимости и занесения в базу СО.
Количество этапов синтеза схемотехнически интегрированных решений определяется возможностью получения новых схемотехнических решений и в пределе может достигать величины n-1. Причем в результате возможна генерация множества решений функционально соответствующих предъявляемым требованиям, но отличающихся схемотехническим исполнением.
Классическим примером синтеза неизбыточного, схемотехнически интегрированного решения является низковольтный стабилизатор напряжения, в котором источник опорного напряжения интегрирован с усилителем сигнала рассогласования [7]. При этом на основе синергетического эффекта удалось синтезировать стабилизатор, обладающий высокой долговременной стабильностью, низким уровнем собственных шумов и сверхмалыми значениями выходного напряжения.
Рецензенты:
- Савельев М.В., д.т.н., профессор кафедры «Электронных вычислительных машин», ГОУ ВПО «Южно-Российский государственный технический университет (НПИ), г. Новочеркасск.
- Галушкин Н.Е., д.т.н., профессор, зав. кафедрой «Прикладная информатика и математика», филиал ФГАОУ ВПО «Южный федеральный университет», г. Новошахтинск.
Работа получена 30.08.2011.



