В современной экономике залогом успешного развития организации является сбалансированное и эффективное управление портфелем инвестиционных активов.
Инвестиционный портфель формируется практически любой компанией среднего и крупного бизнеса. При этом организация стремится включить в портфель только те активы, которые соответствуют ее стратегическим приоритетам, генерируют необходимый денежный поток с допустимым для организации уровнем риска в условиях ограниченного финансирования.
Ограниченность доступных инвестиционных ресурсов как раз и определяет актуальность задачи оптимизации портфеля для любой развивающейся компании и заставляет организацию выбирать из множества активов те, которые соответствуют ожиданиям доходности при установленном уровне риска [1].
Для формирования сбалансированного инвестиционного портфеля вводятся системы ограничений, которые представляют собой некоторые пороговые значения, задающие характеристики будущего инвестиционного портфеля. К объективным ограничениям инвестиционного портфеля можно отнести:
- доступные финансовые ресурсы;
- условие диверсификации инвестиционной деятельности (хеджирование портфеля);
- доходность и самофинансируемость портфеля;
- государственные нормативные требования к реализации инвестиционных проектов.
В задаче оптимизации портфеля перечисленные ограничения образуют допустимое множество решений, то есть допустимое множество инвестиционных активов, которые могут быть включены в портфель в разных долях. С точки зрения процесса формирования портфеля доступные финансовые ресурсы являются наиболее серьезным ограничением. Доступные денежные средства могут не учитываться в математических моделях при нахождении оптимального решения, но тем не менее являются неотъемлемой частью дальнейших инвестиционных решений.
Диверсификация активов или хеджирование портфеля требует включения в портфель как высокорисковых активов, так и активов с минимальными рисками. При этом активы выбираются преимущественно из разных сфер экономики, чтобы еще более снизить эффект от негативных событий. Описание модели портфеля, учитывающей это ограничение, можно встретить в работе [1].
Включение в условия формирования портфеля средств, которые генерируются непосредственно самим инвестиционным портфелем, как правило, учитывается только в динамических моделях оптимизации портфеля и предполагает использование в модели метрик самофинансирования или самоокупаемости актива [2]. Такие модели синхронизации разработки портфеля инвестиций и обеспечения его необходимыми финансовыми ресурсами называют также теоретическими моделями капитала [5].
Совокупность рассмотренных выше условий задает базис для задачи моделирования процесса формирования оптимального портфеля инвестиционных проектов. Структура модели зависит от конкретной постановки задач и цели инвестиционного планирования в организации. Тем не менее именно объективные ограничения инвестиционной деятельности, которые были описаны выше, позволяют построить некоторую практическую модель сбалансированного портфеля инвестиций [3].
При рассмотрении портфеля проекта как объекта моделирования в качестве прототипа была выбрана математическая модель с дополнительными ограничениями [4]. Описанная модель позволяет сформировать инвестиционный портфель с ограничениями сверху, когда доля активов в общей структуре может составлять не более заданной величины. В качестве меры риска портфеля рассматривается стандартное отклонение (или дисперсия), характеризующее вероятность отклонения доходности портфеля от ожидаемого значения. Любой портфель характеризуется двумя параметрами: ожидаемой эффективностью и риском.
Цель работы заключается в модификации описанной методики с помощью ввода дополнительных ограничений на минимальные значения долей активов в портфеле. Для формирования портфеля выбирается пул ценных бумаг - акции и облигации российских компаний - и проводятся предварительные вычисления: расчет доходности и статистических характеристик для каждого актива. Для расчета доходности акций используются временные ряды цен закрытия.
Полученные ряды доходностей используются для расчета математического ожидания и среднего квадратического отклонения доходности ценных бумаг, корреляционной матрицы доходностей активов. Далее устанавливаются необходимые ограничения: заданная доходность портфеля, ограничение на максимальную и минимальную долю каждого актива в портфеле и ограничение на минимальную возможную размерность лота.
Исходная задача представляет собой проблему квадратичного программирования, для решения которой разработаны специальные численные методы. Для конечного последовательного перебора всех возможных опорных планов предлагается воспользоваться алгоритмом перебора с возвратами, который также называется алгоритмом Гамильтона, и применить его на каждом этапе симплексного преобразования. Задача минимизации риска портфеля осуществляется при заданной доходности, начиная от нулевой и до ожидаемой доходности портфеля.
Для проведения вычислительного эксперимента случайным образом было отобрано 10 видов ценных бумаг - акций и облигаций, которые котируются на российской фондовой бирже. Минимальное возможное значение риска для рассматриваемого экспериментального портфеля составляет 10% при отсутствии пороговых ограничений при условии, что доля каждой ценной бумаги не может быть более 35% (табл 1). При малой эффективности в портфель включаются наиболее эффективные облигации в максимальных долях (пороговое ограничение 35%). Например, при заданной эффективности в 10% облигации составляют 98% всего портфеля инвестора.
Таблица 1 - Результаты решения задачи оптимального портфеля
|
# |
mp |
Vp |
x1 |
x2 |
x3 |
x4 |
x5 |
x6 |
x7 |
x8 |
x9 |
x10 |
|
1 |
10% |
0.19 |
0.00% |
0.00% |
0.28% |
0.37% |
1.13% |
35.00% |
35.00% |
0.00% |
28.19% |
0.00% |
|
2 |
15% |
1.92 |
0.00% |
0.00% |
1.93% |
0.76% |
4.82% |
35.00% |
35.00% |
0.00% |
22.49% |
0.00% |
|
3 |
20% |
5.68 |
0.00% |
0.00% |
3.44% |
1.11% |
8.54% |
35.00% |
27.86% |
0.00% |
24.06% |
0.00% |
|
4 |
30% |
19.32 |
0.00% |
0.00% |
6.40% |
1.79% |
15.98% |
35.00% |
6.41% |
0.00% |
34.43% |
0.00% |
|
5 |
50% |
71.04 |
0.00% |
0.00% |
12.68% |
3.21% |
30.76% |
35.00% |
0.00% |
0.00% |
18.35% |
0.00% |
|
6 |
65% |
136.20 |
0.00% |
0.00% |
23.47% |
9.74% |
35.00% |
0.00% |
16.03% |
0.00% |
15.76% |
0.00% |
Преобладающая доля облигаций в портфеле объясняется тем, что облигации традиционно считаются менее рисковым активом, чем акции. Акции корпораций являются не только менее надежными, но и более доходными ценными бумагами. Поэтому невысокая требуемая доходность обеспечивается в основном за счет облигаций, почти без добавления акций, при этом достигается минимизация риска.
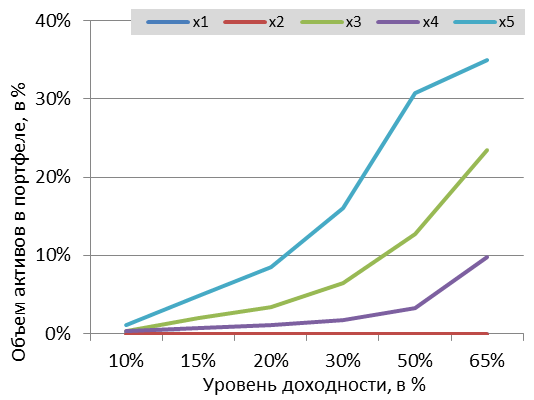
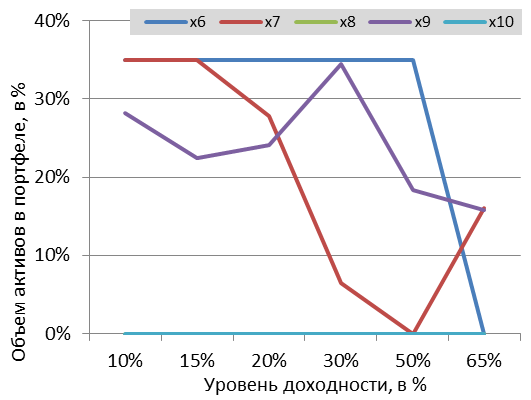
С увеличением эффективности постепенно понижается доля облигаций в портфеле и возрастает доля акций. Для максимальной эффективности (65%) следует вложить капитал в акции, которые обладают высокой доходностью, и в облигации с низким риском. Процесс перераспределения капитала между акциями и облигациями показан на рис. 1 и 2.
|
Рис. 1. Распределение акций в портфеле. |
Рис. 2. Распределение облигаций в портфеле. |
Полученные доли ценных бумаг в инвестиционном портфеле соответствуют классическим распределениям активов при рыночной стратегии минимизации рисков. Таким образом полученные значения распределения долей могут быть использованы для формирования реального инвестиционного портфеля организации с действующими ограничениями.
Указанный метод полного последовательного перебора всех возможных базисных решений подходит только для решения задач с небольшой размерностью. С ростом размерности задачи количество допустимых базисных решений резко возрастает, что увеличивает время обработки. В этом случае предлагается воспользоваться элементами метода Монте-Карло.
Рецензенты
- Сидоренко С.В., д.э.н., начальник Отдела по интеграции науки и образования РАН, г. Москва.
- Галушкин А.И., д.т.н., профессор, начальник лаборатории «Интеллектуальные информационные системы» Федерального государственного научного учреждения «Центр информационных технологий и систем органов исполнительной власти», г. Москва.