Эксплуатация заглубленных в грунт низкотемпературных продуктопроводов требует решения проблем, связанных с обеспечением их устойчивости. Тепловое взаимодействие транспортируемого газа с окружающей грунтом может вызвать так называемое вторичное пучение, которое может нарушить устойчивость трубопровода. Цель данной работы: моделирование теплового поля вокруг трубопровода, транспортирующего продукт с температурой ниже нуля, а также установление места образования прослоев льда и их размеров. По результатам численного расчета даются рекомендации для предотвращения пучения.
Вокруг заглубленного в грунт низкотемпературного трубопровода образуется зона промерзания, в которой может развиваться пучение. Вследствие пучения возможно выпирание трубопровода в сторону дневной поверхности и другие виды нарушении устойчивости трубы.
Характер выделения льда вокруг трубопровода зависит от большого числа факторов: свойств грунта, температурного градиента, условий миграции влаги, вида нагрузки, приложенной к поверхности и т.д. В тонкодисперсных породах вокруг трубопровода в промерзших массивах грунта возможна сегрегация льда за счет миграции незамерзшей влаги к фронту промерзания. При этом частицы грунта раздвигаются кристаллами льда, из микропор агрегатов частиц отжимается вода, которая превращается в лед. В начале промерзания питание растущих прослоев льда происходит в основном за счет собственных запасов грунтовой влаги талой зоны, находящейся вблизи фронта промерзания, а в следующем - за счет внешнего потока влаги. Лед, выделившийся в виде линз и прослоек различной формы и ориентировки, называют ледяными шлирами.
Вокруг холодного трубопровода, заглубленного в дисперсный грунт, практически постоянный температурный градиент существует в течение многих лет. Тепловые потоки, обуславливающие миграцию влаги, малы и практически постоянны, но за длительное время эксплуатации трубопровода суммарный объем сегрегированного льда может быть значительным, и последствия могут быть негативными. Такое пучение грунта в зарубежной литературе [6] называют вторичным.
Для обоснования температуры охлаждения продукта, режимов регулирования температуры продукта во времени и по поверхности теплообмена необходимо располагать методикой тепловых расчетов трубопроводов, учитывающей динамику изменения температуры продукта и окружающей среды (грунта и воздуха). В работе [1] изложена физико-математическая модель явления вторичного морозного пучения вокруг холодных труб, позволяющая проследить механизм развития шлиров в тонкодисперсных материалах, поры которых заполнены влагой и не содержат воздуха, при отсутствии внешних механических нагрузок.
Математическая постановка задачи прогнозирования теплового режима вокруг подземного трубопровода для области, представленной на рис.1, имеет вид нелинейного уравнения теплопроводности:
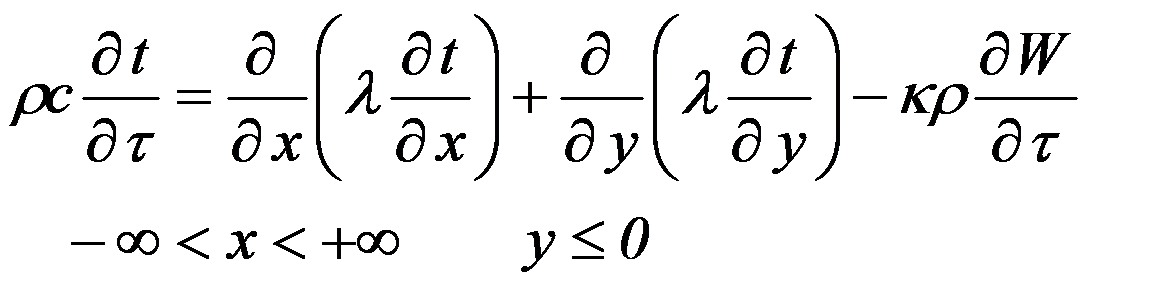(1)
где фазовый переход влаги учитывается последним слагаемым в правой части, 
соответственно температура, координаты, время, удельная теплоемкость, коэффициент теплопроводности, объемный вес скелета грунта, теплота фазового перехода и влажность грунта.
Начальное условие:
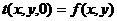(2)
Граничные условия (рис.1) имеют следующий вид:
на Г1: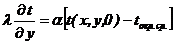 
; (3)
где a-теплоотдача от поверхности грунта; 
; 
;
на Г2: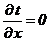 
; на Г3: 
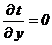; на Г4: 
; на Г5: 
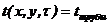. (4)
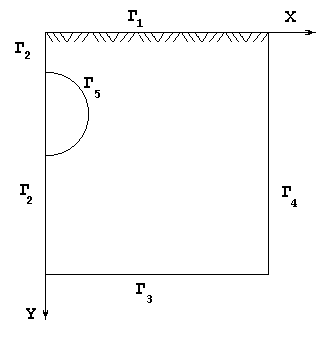
Рис.1.Схема расположения трубопровода в грунте
В тонкодисперсных грунтах, благодаря наличию незамерзшей влаги, резкого фронта фазового перехода не существует и их теплофизические свойства описываются гладкой функцией от температуры. Для определенного вида грунта содержание незамерзшей воды при условиях, близких к термодинамическому равновесию, зависит только от температуры: 
.
Тогда уравнение (1) преобразуется следующим образом
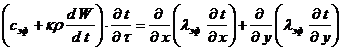, (5)
где 
- соответственно эффективный коэффициент теплопроводности и эффективная теплоемкость.
Для решения уравнения (5) с приведенными выше начальными и граничными условиями (2)-(4) используется метод аппроксимации дифференциального уравнения разностной задачей [5]. Численное решение полученной системы разностных уравнений на каждом временном шаге проводилось универсальным продольно-поперечным методом с помощью компьютера. Результаты программы были протестированы формулой Г. Карслоу и Дж. Егера [4], определяющей радиус кольцеобразной зоны оттаивания вокруг трубы, в квазистационарном приближении.
Далее по полученному температурному полю, используя методику, изложенную в работе [1], исследуется механизм образования сегрегационного пучения под трубопроводом. Учитывая тот факт, что процессы переноса массы и энергии протекают с существенно разными скоростями (коэффициент влагопроводности в промерзающем грунте, по крайней мере, на порядок меньше, чем коэффициент температуропроводности), следует ожидать, что миграция влаги, вызывающая сегрегацию льда, протекает в температурных условиях, близких к стационарным, что подтверждается экспериментами Э. Д. Ершова [2]. Поэтому уравнение энергопереноса принимает следующий вид (квазистационарное приближение):
, (6)
где значения 
определяются решением уравнения (5) при начальных и граничных условиях вида (2)-(4).
Далее, учитывая тот факт, что шлиры образуются только в мерзлой части грунта, решение уравнений массопереноса сводится к решению задач вида
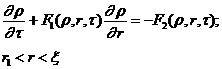(7)
где
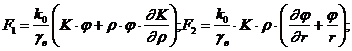
при начальных условиях:
Здесь ξ - граница талой зоны, определенная при решении задачи (2)-(4), а так как талая зона исключается при образовании шлиров, то на ее границе выполняется
(8)
В результате решения задачи (6)-(8) могут получаться области, где 
, т.е. прослои чистого льда. Коэффициент влагопроводности зависит главным образом от плотности грунта и определяется следующим образом 
[4].
Так как непосредственное интегрирование уравнения (7) затруднено, то полученная задача решается методом характеристик [3], т.е. вместо (7) записывается система обыкновенных дифференциальных уравнений:
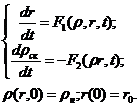
Пересечению характеристик соответствует наложение слоев грунта друг на друга, чем вызвано резкое увеличение плотности, резкое увеличение коэффициента влагопроводности 
и образование шлира.
Графики показывают (рис. 2) , что вокруг холодного газопровода (при 
) после его закладки в теплый грунт образуются прослои льда в короткий промежуток времени на расстоянии 8-12 см от трубы, а позднее (рис. 3) возникает еще один прослой под трубой на расстоянии 90-100 см.
ρ
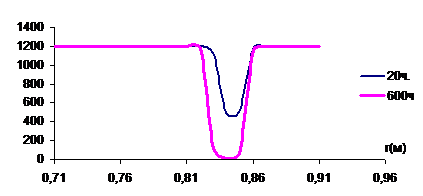
Рис. 2. Графики образования прослоев льда на поверхности трубы при 
ρ
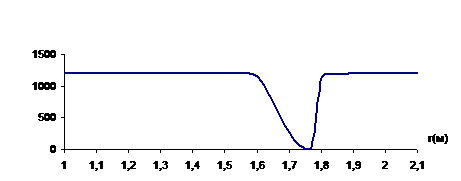
Рис. 3. График образования шлира под трубой с
Исследован процесс образования шлиров для различной температуры трубопровода, транспортирующего охлажденный газ. Результаты показали, что чем ниже температура, тем глубже находится зона образования второго пучения под трубой. При 
второй прослой образуется на расстоянии 50-60 см от трубы, а при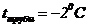 
шлир появляется только на поверхности трубы (рис.4).
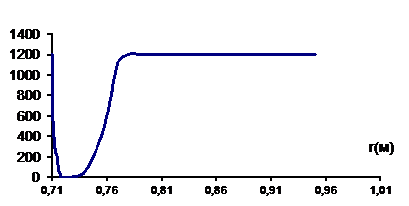
Рис.4. График образования шлира под трубой с
По результатам расчета можно внести следующие технические рекомендации для предотвращения пучения. Если температура газа ниже минус 2 0С, то для устранения пучения нужно увеличить траншею, предназначенную для укладки трубопровода в грунт, до 100 см по радиусу трубы (в зависимости от температуры газа) и засыпать ее непучинистым грунтом.
Другим вариантом является улучшение теплоизоляции трубопровода с тем, чтобы температура на его поверхности была не ниже минус 2 0С. Тогда объем грунта, который нужно менять, значительно уменьшается. Выбор одного из этих вариантов должен быть обоснован технико-экономическим расчетом.
Рецензенты:
- Миронов Виктор Владимирович, д.т.н., профессор, проректор по научной и инновационной работе ТюмГАСУ, г. Тюмень.
- Чекардовский Михаил Николаевич, д.т.н., профессор, заведующий кафедрой «Теплогазоснабжения и вентиляции» ТюмГАСУ, г. Тюмень.