В системах спутниковой связи для формирования требуемых зон покрытия на земной поверхности при заданной области гарантированного уровня сигнала (ГУС) широкое применение получили многолучевые зеркальные антенны (МЛЗА). Одним из этапов проектирования МЛЗА является решение задачи по обеспечению зависящей от геометрооптических параметров антенной системы (АС) требуемой развязки между парциальными лучами, формируемыми излучателями облучающей антенной решетки (ОАР).
Целью статьи является разработка алгоритма оценки величины развязки между парциальными лучами МЛЗА и анализ влияния параметров конфигурации АС на величину развязки между парциальными лучами.
Постановка задачи
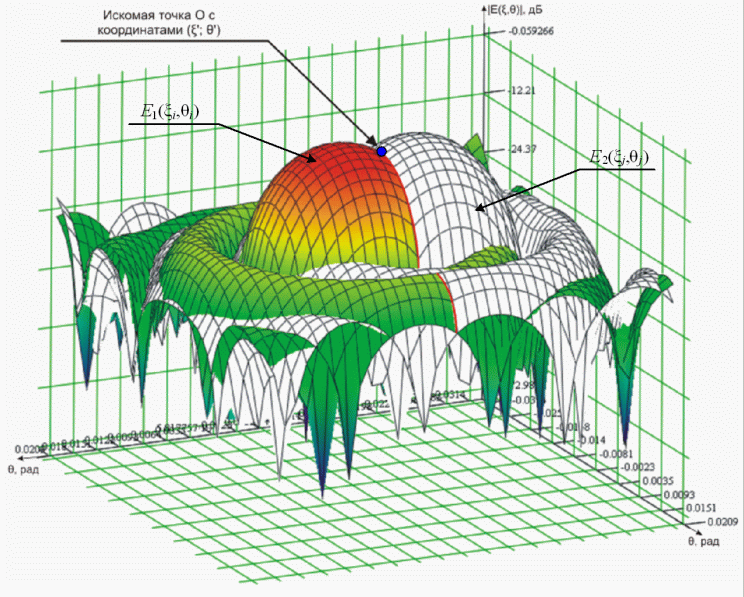
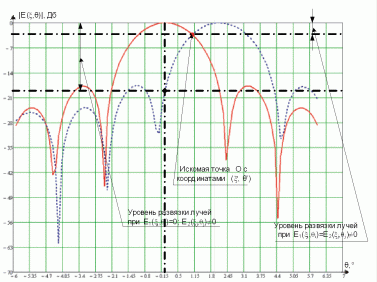
Геометрия задачи представлена на рисунке 1. Определение величины развязки между парциальными лучами МЛЗА для фиксированных значений E1(θi, ξi) и E2(θj, ξj) сводится к поиску точки пересечения между лучами - диаграммами направленности (ДН) антенны от выбранных излучателей для основного вида поляризации (точка O, рисунок 1).
В общем виде задачу определения величины развязки можно свести к задаче поиска экстремума при наличии ограничения в виде равенств [5] либо к задаче поиска максимума со связанными переменными [6].
|
|
|
|
a |
б |
Рис. 1. Геометрическое представление задачи по определению величины развязки между парциальными лучами: a - трехмерное представление ДН; б - двумерное представление среза ДН.
В случае определения величины развязки при постановке задачи поиска экстремума с ограничениями в виде равенств необходимо максимизировать функцию f(ξ,θ):
|
|
(1) |
,
при ограничении в виде равенства
|
|
(2) |
,
где 
, 
- амплитуды векторов электрического поля антенны для основного вида поляризации 1-го и 2-го кластеров соответственно.
В выражении (1) 
- амплитуда вектора электрического поля антенны для основного вида поляризации любого из двух выбранных кластеров (1-го или 2-го).
Определение величины развязки при постановке задачи поиска максимума со связанными переменными в виде
|
|
(3) |
;
требует в заданной медианной плоскости сечения ДН (луча) изменения угла θ = varia на интервале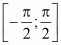 
с условием, что ξ = const для определения минимума функции F(ξ,θ), характеризующей величину невязки между амплитудами электрического поля антенны от 1-го и 2-го кластеров для основного вида поляризации, т.е. является функцией невязки:
|
|
(4) |
.
В ситуации, когда общая задача определения величины развязки сводится к расчету величины развязки между двумя парциальными лучами антенны от двух излучателей из ОАР, исходную постановку можно упростить до решения одномерной безусловной оптимизационной задачи поиска минимума целевой функции:
|
|
(5) |
.
Значение сферического угла ξ' определяется выражением
|
|
(6) |
,
где x1, y1; x2, y2 - координаты центров 1-го и 2-го излучателей в системе координат ОАР.
Решение задачи (5) методами оптимизации первого (метод градиентного спуска, наискорейшего градиентного спуска, сопряжённых градиентов и т.д.) или второго порядка (метод Ньютона, Ньютона-Рафсона, Марквардта и др.) [2] требует вычисления первой и второй производной целевой функции:
|
|
(7) |
|
|
(8) |
,
,
где значение электрического поля 
антенны от любого излучателей определяется с помощью выражения [1]:
|
|
(9) |
,
где 
- орт нормали к поверхности в точке интегрирования; 
- вектор плотности поверхностного тока в точке интегрирования рефлектора; 
- вектор напряженности магнитного поля излучателя в точке интегрирования, a - размер большой полуоси рефлектора, 
- фазовый множитель, рассчитываемый согласно выражению
|
|
(10) |
,
где xo, yo, zo - координаты излучателя в общей системе координат рефлектора; x' - клиренс; 
, 
, 
- координаты точки интегрирования на рефлекторе, соответствующие направлениям по осям OX, OY, OZ, причем Z - определяет поверхность отражения рефлектора произвольного профиля в виде 
, где, например,
|
|
(11) |
,
Z, x, y - координаты точки на рефлекторе для параболоида, а f - фокусное расстояние.
В связи с большой вычислительной сложностью градиента и гессиана целевой функции (5) от интеграла по поверхности (9) для определения величины развязки между излучателями облучающей антенной решетки многолучевой зеркальной антенны по характеристике излучения антенны в дальней зоне, по-моему мнению, наиболее целесообразным является применение оптимизационных методов нулевого порядка (дихотомии, золотого сечения, Фибоначчи и др.), не требующих вычисления первой и второй производных целевой функции и позволяющих достигнуть эффективного решения оптимизационной задачи с использованием лишь значения функции на исходном интервале с заданной погрешностью вычисления.
Алгоритм решения задачи
Поиск минимума целевой функции (5) произведем гибридным методом одномерной безусловной оптимизации, представляющим собой комбинацию методов нулевого порядка Фибоначчи [4] и параболической интерполяции [5], и обладающим высокой надежностью и гарантированной сходимостью. Причем предлагаемая модификация известных методов нулевого порядка обеспечивает сверхлинейную скорость сходимости в окрестности точки минимума целевой функции (5). В методе Фибоначчи на каждой итерации стратегия сокращения интервала неопределенности при заданном количестве вычислений функции K опирается на числа последовательности Фибоначчи, определяющейся из выражения
|
|
(12) |
, 
имеющей вид: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233 ...
Алгоритм решения оптимизационной задачи (5) заключается в следующем.
Шаг 1. Задается начальный интервал неопределенности угла 
и выбирается допустимая длина конечного интервала 
(точность достаточно задавать порядка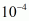 
- 
), определяющая погрешность вычисления угла 
. При этом границы интервала неопределенности 
и 
должны задаваться углами отклонения прихода плоской волны с направлений, соответствующих фазовым центрам для 1-го и 2-го облучателя соответственно. К примеру, для осинесимметричного рефлектора параболической формы угол отклонения 
прихода плоской волны с направления, соответствующего фазовому центру облучателя, расположенного в плоскости O'X'Y' системы координат ОАР O'X'Y'Z' в точке A (x,y), смещенной от центра ОАР, расположенного в точке фокуса рефлектора, причем ориентация ОАР определяется углом 
( 
- угол между фокальной осью рефлектора OZ и вектором нормали плоскости ОАР), рассчитывается в соответствии с соотношением
|
|
(13) |
,
где D - диаметр рефлектора; x' - клиренс; f - фокус рефлектора.
Шаг 2. Рассчитывается по правилу (12) вектор последовательности чисел Фибоначчи размерности K (задает максимально допустимое число итераций расчета при решении оптимизационной задачи).
Шаг 3. Положить k = 0.
Шаг 4. Вычислить 2 точки внутри интервала по правилу 
Шаг 5. Рассчитать значения целевой функции (5) в полученных точках 
, 
и на границах интервала неопределенности 
, 
.
Шаг 6. Вычислить 2 точки внутри интервала по правилу
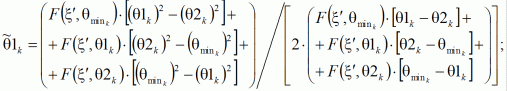
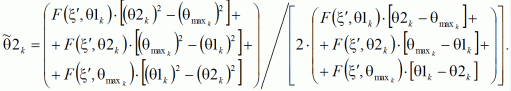
Шаг 7. Рассчитать значения целевой функции (5) в полученных точках 
и 
.
Шаг 8. Сравнить 
с 
:
а) если 
, положить 
; 
и перейти к шагу 9.
б) если 
, положить 
; 
.
Шаг 9. Проверить условие окончания и в случае необходимости сделать заключительное K-е вычисление функции (5) для получения решения:
а) если 
, положить k = k+1 и перейти к шагу 4;
б) если 
, то отсутствует точка нового вычисления функции (5). Следует положить: 
; 
. В точках 
и 
вычисляется значение функции и находятся границы конечного интервала неопределенности.
Процесс поиска завершается и 
. В качестве приближенного решения искомый угол 
, удовлетворяющий (5), выбирается на середине рассчитанного интервала.
Таким образом, предложенный алгоритм определения величины развязки между парциальными ДН МЛЗА является решением оптимизационной задачи по поиску минимума целевой функции с заданной точностью ε1. Результатом выполнения данного алгоритма является значение сферического угла θ', удовлетворяющее условию (5). На практике решение интеграла (9) осуществляется численным методом с помощью квадратурных формул Гаусса [3].
В результате оценки вычислительной сложности предложенного алгоритма получен график, представленный на рисунке 2, отражающий зависимость количества вычислений целевой функции (5) от величины допустимой длины конечного интервала (погрешности вычисления) 
для предложенного алгоритма и алгоритмов одномерной оптимизации известных методов нулевого порядка: дихотомии, золотого сечения, Фибоначчи и квадратичной интерполяции (рис. 2).
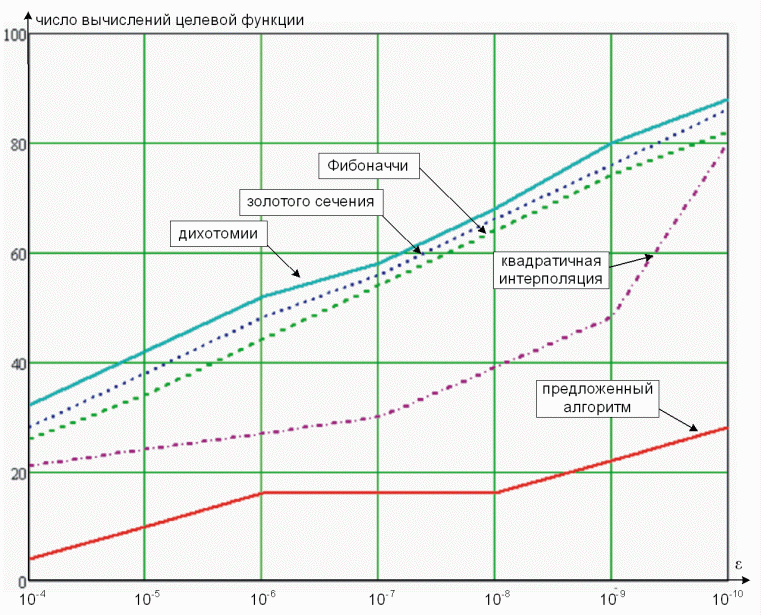
Рис. 2. Зависимость количества вычислений целевой функции от погрешности вычисления при решении оптимизационной задачи (5) предложенным алгоритмом, дихотомии, золотого сечения, Фибоначчи и квадратичной интерполяции.
Таким образом, предложенное решение доставляет минимум целевой функции (5) в случае равенства допустимой длины конечного интервала 
за 4-5 итераций (что соответствует, для предложенного алгоритма, 22-28 вычислениям целевой функции (5)), в то время как решение оптимизационной задачи (5) стандартными алгоритмами одномерной безусловной оптимизации нулевого порядка (дихотомии, золотого сечения, Фибоначчи, полиномиальной аппроксимации) [4] определяют минимум целевой функции в лучшем случае за 40-45 итераций (что соответствует 80-90 вычислениям целевой функции (5)).
Результаты решения задачи
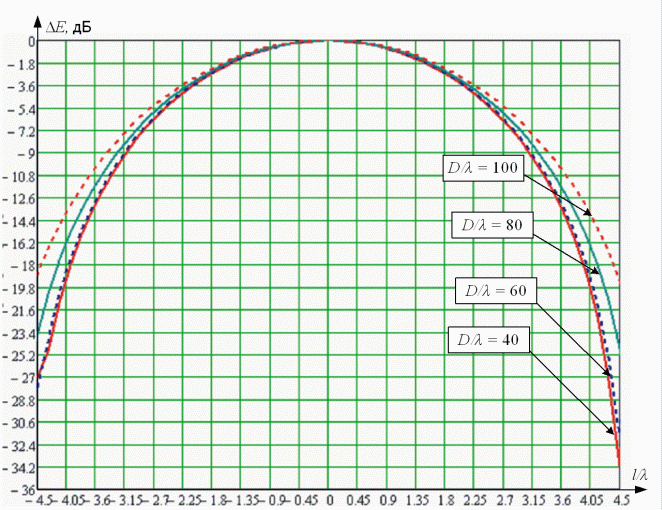
Анализ влияния величины развязки между парциальными лучами производился для следующих исходных геометрооптических параметров АС: осинесимметричный рефлектор параболической формы с отношением клиренса x' к длине волны λ, равным 6; длина волны λ = 0,05 м; отношение радиуса конического рупорного излучателя d к длине волны λ равно 1; отношение фокусного расстояния f к диаметру рефлектора D равно 1,73; отношение диаметра рефлектора D к длине волны λ равно 30.
Расчеты были произведены при размещении одного из излучателей в фокусе антенны (точки с координатами (0; 0; f) в системе координат рефлектора OXYZ) и смещении другого на величину Δ, определяемую из отношения расстояния между центрами рупорных излучателей l к длине волны λ от -4,5 до 4,5 с шагом h = 0,2 по осям O'X', O'Y' и по диагоналям, расположенным к оси O'X' под углами 45 и 135° в плоскости O'X'Y' в системе координат ОАР (O'X'Y'Z').
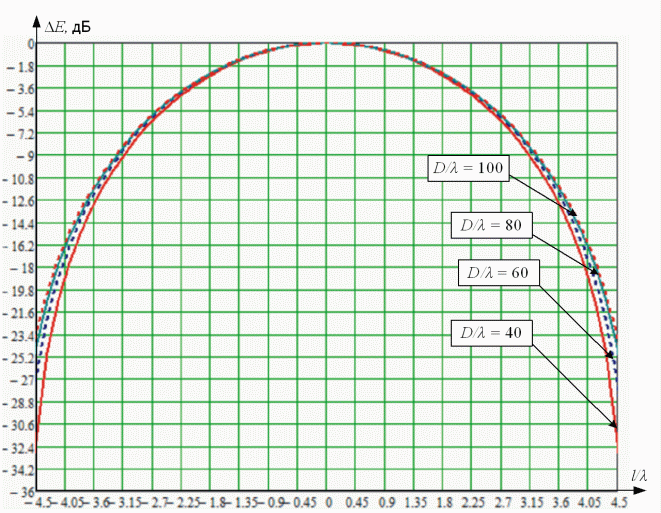
На рисунке 3 представлены графики зависимости величины развязки между формируемыми парциальными лучами от изменения расстояния между центрами рупорных излучателей по оси O'X' (ξ' = 0°), O'Y' (ξ' = 90°) при изменении длины волны λ на величину, соответствующую изменению соотношения 
100, 80, 60, 40.
|
|
|
|
а |
б |
Рис. 3. Результат расчета величины развязки при смещении излучателя:
а - по оси O'X'; б - по оси O'Y'.
Выводы
Предложенный алгоритм расчета величины развязки между излучателями ОАР МЛГЗА по характеристике антенны в дальней зоне позволяет с заданной погрешностью вычисления ε1 за конечное число итераций K определить искомую точку O с координатами (θ', ξ') в исходной постановке задачи (рис. 1). Предложенное решение и выбор начальных приближений (определение интервала неопределенности) (13) позволяет существенно снизить вычислительную сложность решения общих задач (1) и (3). Из приведенных результатов расчета (на графиках) видно, что при увеличении величины отношения диаметра рефлектора D к длине волны λ график развязки между парциальными лучами расширяется, а, следовательно, увеличивается величина помех между формируемыми зонами покрытия на земной поверхности антенны соседними излучателями при приеме/передаче сигнала на одной частоте. Причем в ситуации смещения излучателя по оси O'X' (рис. 3а) изменение величины развязки более чувствительно к изменению рабочей частоты (длины волны) в отличие от ситуации, когда смещение излучателя производится по оси O'Y' (рис. 3б), что объясняется осинесимметричной поверхностью рефлектора и прямо пропорционально зависит от величины отношения клиренса антенны к длине волны.
Рецензенты:
- Архипов Н.С., доктор технических наук, доцент, сотрудник Академии ФСО России, г. Орел.
- Батенков А.А., доктор технических наук, профессор, сотрудник Академии ФСО России, г. Орел.
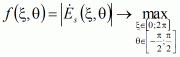
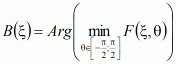
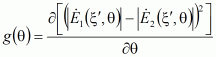
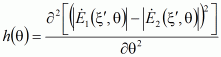
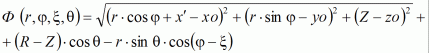
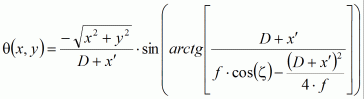