Одна из ключевых тенденций современной науки связана со сложностью изучаемых объектов. Если раньше исследователи могли анализировать лишь точно описываемые явления и процессы с малым числом переменных, то с развитием теоретического знания и информационных технологий появилась возможность исследования нового класса систем, получивших общее название - сложные технические системы.
Для построения систем автоматического управления сложными нелинейными, плохо формализуемыми объектами часто применяют устройства и алгоритмы управления, выполненные на основе методов нечеткой логики (фаззи-логики). Эти методы принципиально отличаются от обычных классических методов автоматики «человеческим» подходом и «человеческими» приемами решения задач управления.
Теория нечетких множеств, основные идеи которой были предложены американским математиком Лотфи Заде (Lotfi Zadeh) более 40 лет назад, позволяет описывать качественные, неточные понятия и наши знания об окружающем мире, а также оперировать этими знаниями с целью получения новой информации. Основанные на этой теории методы построения информационных моделей существенно расширяют традиционные области применения компьютеров и образуют самостоятельное направление научно-прикладных исследований, которое получило специальное название - нечеткое моделирование.
Общей предпосылкой для применения нечетких систем управления является, с одной стороны, наличие неопределенности, связанной как с отсутствием информации, так и сложностью системы и невозможностью или нецелесообразностью ее описания традиционными методами и, с другой - наличие объекта, необходимых управляющих воздействий, возмущений и т.п., а также наличие информации качественного характера.
Типичный колесный робот, например, Американская компания «MobileRobots» представила мобильный робот P3-DX (на рис. 1). Мобильный робот представляет собой трехколесную платформу, снабженную независимыми электродвигателями правого и левого колеса. На платформе установлена видеокамера и ультразвук.
Кинематическая модель колесного робота P3-DX является следующим видом:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
где
![]() -координат колесного робота на плоскости,
-координат колесного робота на плоскости,
![]() -угол поворота робота в плоскости,
-угол поворота робота в плоскости,
![]() - скорость робота,
- скорость робота,
![]() - угловой скорости,
- угловой скорости,
![]() -продольная скорость колеса,
-продольная скорость колеса,
![]() -коэффициент передачи привода.
-коэффициент передачи привода.
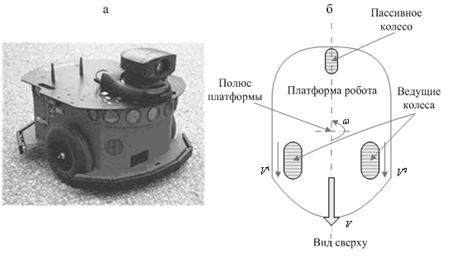
Рис. 1. (a) Внешний вид мобильного робота P3-DX; (б) мобильный робот P3-DX, вид сверху
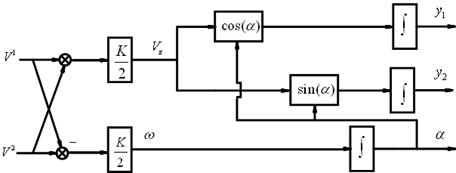
Рис. 2. Кинематическая модель колесного робота P3-DX
Мобильным управляемым объектом в разработанном отладочном комплексе является колесный робот. В общем случае задача его локализации (определения его декартовых координат ![]() и угловой ориентации α в момент t) (рис.3.) может быть решена путем непосредственного обнаружения и распознавания.
и угловой ориентации α в момент t) (рис.3.) может быть решена путем непосредственного обнаружения и распознавания.
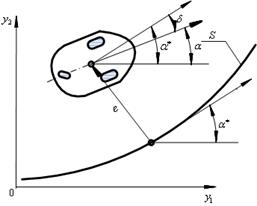
Рис. 3. Колесный робот и отрезок кривой S. e- отклонение по нормали от кривой S, δ- ошибка угловой ориентации
Если рассматривать нечеткий регулятор как "черный ящик", то он ничем не отличается от классических регуляторов и структура нечетких систем управления строится по классическим образцам (рис. 4.).
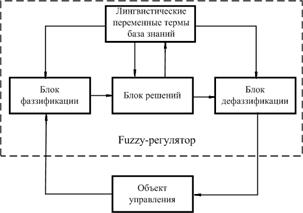
Рис. 4. Функциональная схема системы с нечеткой логикой
К настоящему времени предложено несколько алгоритмов нечеткого вывода. Некоторые из них получили наибольшее применение в системах нечеткого вывода, в том числе алгоритм Мамдани, алгоритм Цукамото, алгоритм Ларсена, алгоритм Сугено и.д. Мы выбираем алгоритм Мамдани.
Алгоритм Мамдани является одним из первых, который нашел применение в системах нечеткого вывода. Формально алгоритм Мамдани может быть определен следующим форме (на рис. 5).

Рис. 5. Система нечеткого вывода Мамдани
Все системы с нечеткой логикой функционируют по одному принципу: показания измерительных приборов фаззифицируются, обрабатываются, дефаззифицируются.
Формально алгоритм Мадани может быть определен следующим образом.
- 1. Формирование базы правил систем нечеткого вывода.
- 2. Фаззификация входных переменных.
- 3. Агрегирование подусловий в нечетких правилах продукций.
- 4. Активизация подзаключений в нечетких правилах продукций.
- 5. Аккумуляция заключений в нечетких правил продукций
- 6. Дефаззификация выходных переменных.
Формирование базы правил систем нечеткого вывода
В качестве входных переменных выберем "отклонение по нормали" и "ошибка угловой ориентации", вычисленные в ближайшей к роботу точке траектории. На выходе будем определять безразмерные переменные характеризующие "желаемые скорости и желаемая угловая скорость".
Для всех входных и выходных переменных построим лингвистические переменные.
![]() "Отклонение по нормали"
"Отклонение по нормали"
Термы: отрицательная большая; отрицательная малая; нулевая; положительная малая; положительная большая.
![]() "Ошибка угловой ориентации"
"Ошибка угловой ориентации"
Термы: отрицательная большая; отрицательная средняя; отрицательная малая; нулевая; положительная малая; положительная средняя; положительная большая.
![]() "Желаемая скорость"
"Желаемая скорость"
Термы: нулевая; малая; средняя; большая.
![]() "Желаемая угловая скорость"
"Желаемая угловая скорость"
Термы: отрицательная большая; отрицательная средняя; отрицательная малая; нулевая; положительная малая; положительная средняя; положительная большая.
В этом случае система нечеткого вывода будет содержать 17 правил нечетких продукций следующего вида:
ПРАВИЛО #: ЕСЛИ <условия>, ТО<действия >
Например: ПРАВИЛО_1:ЕСЛИ "![]() есть PB"и"
есть PB"и"![]() есть NB"ТО "
есть NB"ТО "![]() есть PS"и"
есть PS"и"![]() есть NM"
есть NM"
Фаззификация входных и выходных переменных
Для рассматриваемого колесного робота выходные переменные - желаемая скорость:![]() "нулевая скорость";
"нулевая скорость";![]() "малая скорость";
"малая скорость";![]() "средняя скорость";
"средняя скорость";![]() "большая скорость". Удобно задать графически с помощью кусочно-линейных функций принадлежности. Один из возможных конкретных вариантов этих нечетких множеств изображен на рис. 6.
"большая скорость". Удобно задать графически с помощью кусочно-линейных функций принадлежности. Один из возможных конкретных вариантов этих нечетких множеств изображен на рис. 6.
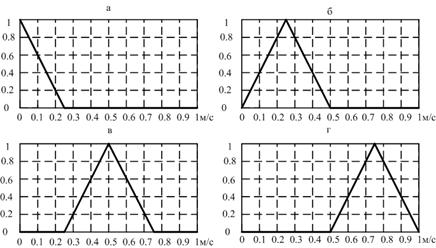
Рис. 6. Графики функций принадлежности нечетких множеств соответствующих нечетким переменным ![]() "нулевая скорость" (а),
"нулевая скорость" (а), ![]() "малая скорость" (б),
"малая скорость" (б), ![]() = "средняя скорость" (в),
= "средняя скорость" (в), ![]() = "высокая скорость" (г).
= "высокая скорость" (г).
Аналогично, можно все четыре графика представить на рис. 7, что позволяет сравнивать значения функций принадлежности соответствующих нечетких переменных для различных значений универсума.
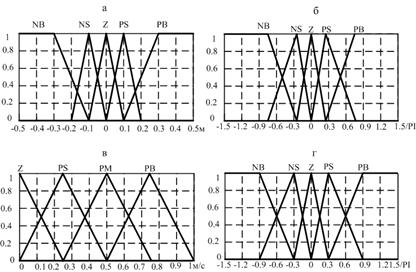
Рис. 7. Графики функций принадлежности колесного робота (а) ![]() - "Отклонение по нормали";(б)
- "Отклонение по нормали";(б) ![]() - "Ошибка угловой ориентации";(в)
- "Ошибка угловой ориентации";(в) ![]() - "Желаемая скорость";(г)
- "Желаемая скорость";(г) ![]() - "Желаемая угловая скорость".
- "Желаемая угловая скорость".
Агрегирование, Активизация и Аккумуляция
Если предположим, что базу знаний образуют два нечётких правила:
П1: если х есть А1 и y есть В1, то z есть С1,
П2: если х есть А2 и y есть В2, то z есть С2,
Сначала находят уровни отсечения для предпосылок каждого из правил
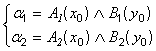 (6)
(6)
где через " ![]() " обозначена операция логического минимума.
" обозначена операция логического минимума.
Потом находят усечённые функции принадлежности:
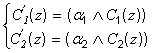 (7)
(7)
Композиция: с использованием операции max (обозначенной как " ![]() ") производится объединение найденных усеченных функций, что приводит к получению итогового нечёткого подмножества для переменной выхода с функцией принадлежности
") производится объединение найденных усеченных функций, что приводит к получению итогового нечёткого подмножества для переменной выхода с функцией принадлежности
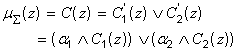 (8)
(8)
Дефаззификация
Для выполнения численных расчетов на этапе дефаззификации могут быть использованы следующие формулы, получившие название методов дефаззификации: метод центра тяжести; метод центра тяжести для одноточечных множеств; метод центра площади; метод левого модального значение и.д. Мы будем пользоваться методом центра тяжести
Центр тяжести рассчитывается по формуле:
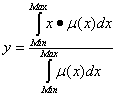 (9)
(9)
где
y - результат дефаззификации;
x -переменная, соответствующая выходной лингвистической переменной ;
![]() -функция принадлежности нечеткого множества, соответствующего выходной переменной ω после этапа аккумуляции;
-функция принадлежности нечеткого множества, соответствующего выходной переменной ω после этапа аккумуляции;
Min и Мах-левая и правая точки интервала носителя нечеткого множества рассматриваемой выходной переменной ω.
Мы определили общую структуру системы нечеткого управления колесным роботом (на рис. 8).
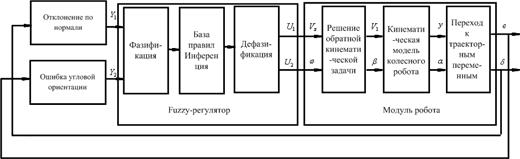
Рис. 8. Структура системы нечеткого управления колесным роботом
После определения, таким образом, системы нечеткого вывода было проведено моделирование ее робота на тестовом наборе данных. Полученные результаты расчета показаны рис. 9.
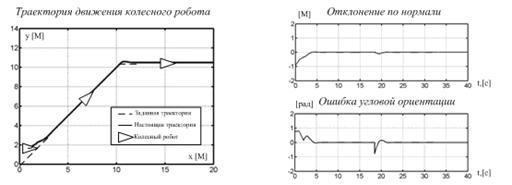
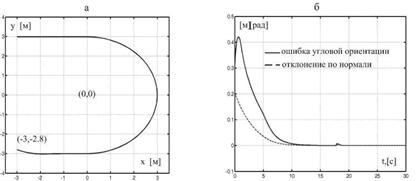
Рис. 9. Результаты эксперимента: (а) Движение вдоль линии; (б) Движение вдоль линии и окружности.
Результаты проведенных исследований доказали и подтвердили целесообразность использования принципов нечеткого управления для формирования поведения колесного робота в условиях определенности.
СПИСОК ЛИТЕРАТУРЫ:
-
1. Алтунин А.Е., Семухин М.В. Модели и алгоритмы принятия решений в нечетких условиях. Тюмень: Изд-во Тюменского государственного университета, 2000. - 352 с.
-
2. Бурдаков С.Ф., Мирошник И.В., Стельмаков Р.Э. Системы управления движением колесных роботов//Санкт-Петербург: - "Наука", 2001 .
-
3. Градецкий В.Г., Вешников В.Б., Калиничеко С.В. Управляемое движение мобильных роботов по произвольно ориентированным в пространстве поверхностям. - М.: Наука,2001
-
4. Демидова Л.А., Кираковский В.В., Пылькин А.Н. Алгоритмы и системы нечеткого вывода при решении задач диагностики городских инженерных коммуникаций в среде MATLAB. - М.: Радио и связь, Горячая линия - Телеком, 2005. - 365 с.
-
5. Леоненков А.В., Нечеткое моделирование в MATLAB и fuzzyTECH. //Санкт-Петербург: - «БХВ-Петербург», 2005.



