Введение
Перспективы применения керамических материалов связаны с их механическими, тепловыми и химическими свойствами. Исследование механической прочности керамических материалов на основе оксида алюминия, работающих в экстремальных условиях эксплуатации, представляет не только научный, но и практический интерес, так как их области применения расширяются с каждым годом.
Прочностные свойства материалов особенно чувствительны к структурно-фазовому состоянию, наличию и характеру распределения дефектов структуры. Изменение прочности может быть связано с перераспределением внутренних напряжений в керамических материалах. На прочностные свойства материалов существенно влияют радиационно-индуцированные процессы, такие как высокая неравновесная концентрация точечных дефектов, зарождение и рост вакансионных, межузельных дислокационных петель, эволюция и создание дислокационной структуры и др. [5, 4].
На сегодня остается открытым вопрос, каким образом располагаются радиационные точечные дефекты и дислокации в керамических материалах, поскольку при их создании материалы находятся в условиях, когда могут происходить процессы самоорганизации и образовываться различные упорядоченные структуры радиационных дефектов. В свою очередь наличие таких структур будет влиять на механические свойства материалов. Поэтому теоретический анализ параметров, при которых наблюдается формирование упорядоченных дислокационных структур в керамических материалах, является актуальным. При этом рассматриваемая модель этих процессов позволяет предсказать условия и значения критических параметров, при которых формируется определенная дефектная структура материала.
Целью данной работы является теоретический анализ процесса самоорганизации дислокаций в керамических материалах после воздействия излучения и исследование влияния его на механическую прочность.
Результаты и обсуждение
Дислокационно-кинетический подход к качественному анализу прочности поликристаллических материалов предполагает, что дислокации как элементарные носители пластической деформации вместе с вакансиями определяют все явления в поликристаллических телах, связанные с их прочностью [5].
В более широком аспекте уравнения дислокационной кинетики при надлежащем включении в них структурных факторов могут служить основой при моделировании и прогнозировании прочностных свойств материалов, а также при разработке технологических процессов улучшения их эксплуатационных характеристик.
В работе [2] представлена математическая модель упорядочения дислокаций в кристаллической фазе керамических материалов на основе 
после нейтронного облучения и оценка периода, образующейся при этом решетки плотности дислокаций.
Уравнение для плотности числа дислокаций имеет вид [1, 3]:
(1)
где 
– плотность дислокаций, 
– пространственно-однородный источник генерации дислокаций, определяющий однородную вдоль 
плотность дислокации 
; 
– коэффициент диффузии дислокаций; 
– вектор смещения среды с дислокациями.
Поверхностный слой с большой плотностью дислокаций можно рассматривать как пленку толщины 
на подложке. Будем считать, что ось 
направлена вглубь материала, так что плоскость 
совпадает с границей раздела поверхностного слоя с подложкой.
Деформация пленки выражается через изгибную координату пленки 
, то есть через смещение точек средней плоскости пленки по от равновесного положения. Уравнение для смещения имеет вид [1]
, (2)
где 
; 
– модуль Юнга; 
– коэффициент Пуассона; 
, 
– перпендикулярное к поверхности пленки напряжение.
Изгибная координата связана с деформацией пленки 
как [1]
. (3)
Изгиб пленки вызывает появление деформации среды:
, (4)
где 
– вектор смещения среды, 
– поперечная и продольная скорости звука в подложке, 
, – модуль Юнга; 
– плотность подложки, – коэффициент Пуассона.
На границе раздела пленка-подложка смещение вдоль оси происходит непрерывно, то есть
, (5)
, (6)
где 
– модуль сдвига, 
.
Нормальное напряжение в подложке определяет силу, действующую на пленку по оси
, (7)
где – плотность подложки, 
.
Уравнения (1)–(4) с соответствующими граничными условиями (5)–(7) являются исходными уравнениями для анализа дислокационно-деформационной неустойчивости.
Качественный анализ системы нелинейных уравнений (1)–(4) позволяет получить дисперсионное уравнение, которое позволяет установить связь между инкрементом неустойчивости и волновым вектором Фурье гармоники неоднородного распределения плотности дефектов 
:
, (8)
где 
, 
, 
, , – модуль сдвига.
При 
возникает дислокационно-деформационная неустойчивость с образованием решетки плотности дислокаций, причем период этой решетки 
, где 
– значение 
, при котором достигается максимальное значение инкремента неустойчивости 
. При условии 
из (8) имеем:
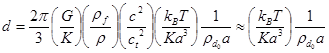. (9)
Неустойчивость гармоники возникает, когда средняя плотность дислокаций превосходит критическое значение:
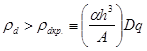. (10)
Рассмотренная модель радиационного упорядочения дислокаций в керамических материалах, основанная на представлениях модели дислокационно-деформационной неустойчивости, адекватно описывает процесс эволюции дислокаций на поверхности образца и позволяет оценить период образующейся структуры в виде (9), при этом учтен в виде добавочного слагаемого в уравнении для плотности числа дислокаций (1) источник генерации дислокаций.
В результате проведенного анализа на неустойчивость получено аналитическое выражение для критического значения плотности дислокаций, при превышении которого происходят процессы упорядочения дислокаций. В свою очередь, процессы самоорганизации дислокаций определяют образование различных дислокационных и деформационных структур в материале, а также характер деформационного упрочнения материала.
Для того чтобы установить влияние плотности дислокаций на механическую прочность керамики, предложено использовать кинетическое уравнение для описания пространственной эволюции дислокаций в условиях облучения. Поскольку прочностные свойства керамических материалов зависят от характера распределения дефектов структуры.
Дислокационный подход к проблеме упрочнения поликристаллических материалов предполагает, что напряжение их пластического течения 
определяется взаимодействием дислокаций друг с другом и с другими препятствиями в решетке в соответствии с известным соотношением Тейлора для дислокационного упрочнения кристаллического материала [5]
, (11)
где – средняя плотность дислокаций в материале, 
– постоянная взаимодействия дислокаций друг с другом, 
– напряжение трения при взаимодействии движущихся дислокаций с решеточными дефектами и различными препятствиями не деформационного происхождения. Справедливость соотношения (11) для поликристаллических материалов проверена на большом их числе вплоть до плотностей дислокаций 1015–1016 м-2 [1]. В (11) фигурирует однородная средняя плотность дислокаций в материале. В случае неравномерного их распределения, например, в виде различных дислокационных структур, эта формула также справедлива, но постоянная взаимодействия дислокаций принимает эффективное значение [5].
В процессе нагружения плотность дислокаций в материале возрастает вследствие работы дислокационных источников и размножения дислокаций. С другой стороны, скорость аккумуляции дислокаций материалом ограничивается процессом аннигиляции дислокаций, который происходит как при низких, так и при умеренных и повышенных температурах. Поликристалличность материала приводит к интенсификации в нем процесса накопления дислокаций, а в случае ультрамелкозернистых материалов к интенсификации процесса аннигиляции дислокаций в границах зерен ввиду возрастающего соотношения между поверхностью зерен и их объемом и сильного укорочения диффузионных расстояний в границах мелкозернистых агрегатов.
Уравнение эволюции средней плотности дислокаций со временем 
в процессе пластической деформации можно записать в следующем общем виде:
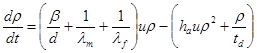, (12)
где 
и 
– соответствующие расстояния свободного пробега дислокаций между актами двойного поперечного скольжения, 
– некоторый коэффициент, – скорость перемещения дислокаций вдоль плоскостей скольжения, 
– характерное расстояние аннигиляции винтовых участков дислокационных петель, 
– характерное время.
В условиях одноосной деформации растяжения или сжатия с постоянной скоростью 
для скорости изменения плотности дислокаций имеем соотношение 
, где 
– скорость сдвиговой деформации, – скорость дислокаций, 
– фактор Тейлора для поликристалла. Подставляя его в (12), получаем уравнение, описывающее изменение средней плотности дислокаций с ростом сдвиговой деформации 
,
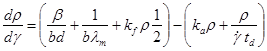, (13)
где 
– коэффициент, определяющий интенсивность размножения дислокаций (
), 
– коэффициент аннигиляции винтовых дислокаций.
Кинетический подход позволяет установить связи между стадиями деформационного упрочнения материала и формирующимися на них дислокационными структурами. Формирование неоднородных дислокационных структур есть следствие пространственно-временной самоорганизации дислокаций в материале.
Выводы
В результате исследования влияния плотности дислокаций на механическую прочность керамики можно сделать выводы:
1. Прочностные свойства керамических материалов зависят от характера распределения дефектов структуры, поэтому предложено использовать кинетическое уравнение для описания пространственной эволюции дислокаций в условиях облучения.
2. На основании уравнения эволюции средней плотности дислокаций в процессе пластической деформации получено кинетическое уравнение, описывающее изменение средней плотности дислокаций с ростом сдвиговой деформации, являющееся основой анализа экспериментальных данных.
Рецензенты:
Ланкин Сергей Викторович, д.ф.-м.н., профессор, заведующий кафедрой физики и методики преподавания физики ФГБОУ ВПО «Благовещенский государственный педагогический университет», г. Благовещенск.
Астапова Елена Степановна, д.ф.-м.н., профессор, профессор кафедры прикладной информатики и математики НОУ ВПО «Благовещенский филиал Московской академии предпринимательства», г. Благовещенск.