Введение
Активное вторжение в область нанотехнологий должно сочетать рассмотрение вопросов, связанных с подготовкой вычислительной среды на атомарном уровне, с представлением различных аспектов классических и неклассических алгоритмов, обеспечивающих возможность эффективного использования такой среды. В этом случае в качестве языка спецификаций и средства описания неклассических алгоритмов может быть использован формализм алгебры гильбертова пространства [4], позволяющий представить совместно описание и своеобразную декомпозицию на элементарные операции. Первые предложения по квантовой логике были сделаны Биркхофом и фон Нейманом [3]. Согласно их подходу, ставшему классическим, значение элементарных экспериментальных положений квантовой теории расценивается как определенные подходящие наборы состояний квантовых объектов. Так как эти наборы должны удовлетворить некоторым специальным замкнутым условиям, то в структуре традиционной квантовой логики положения могут быть адекватно интерпретируемы как подпространства гильбертова пространства, связанного с исследуемой физической системой.
В классической теории состояние определяется заданием всех координат и скоростей составных частей системы в определенный момент времени. В квантовой теории квантовое состояние – это полный набор данных (физических величин), определяющих свойства системы. Какие именно данные определяют состояние – зависит от конкретной системы. Так как состояние – совокупный набор данных, то можно сказать, что состояние есть объект типа «вектор» в Гильбертовом пространстве.
Простейшим является пространство двух базовых состояний – квантовый бит (кубит). В квантовой теории информации кубит определяется как единица квантовой информации, аналогично тому, как бит определяется как единица в классической теории информации.
Главным отличием квантового двухуровневого элемента (кубита) от классического бита с двумя булевыми состояниями 0 или 1, принимаемыми с вероятностями либо P(0) = 1, либо P(1) = 1, является способность кубита находиться одновременно сразу в обоих своих базисных состояниях, т. е. образовывать когерентную суперпозицию базисных квантовых состояний, которая в случае чистого (когерентного) квантового состояния описывается одним из двух эквивалентных способов, а именно:
а) вектором состояния (это спинор первого ранга в двумерном гильбертовом пространстве состояний, в котором базисные векторы состояний играют роль единичных ортогональных векторов – ортов), представляемым двухрядной матрицей-столбцом: 
, 
, где 
– комплексные амплитуды, 
, 
– вероятности, с которыми спин находился в базисных состояниях 
и 
(для записи векторов используется нотация Дирака). Вектор состояния характеризуется тремя независимыми вещественными параметрами (по 2 вещественных числа на 
и 
без одного, обусловленного наличием ограничения );
б) матрицей плотности (матрица плотности была введена фон Нейманом [3] для описания статистических концепций в квантовой механике. Данное представление дает возможность избежать введения лишних переменных и экономным способом описать всю доступную информацию о системе):
, 
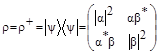, где 
– знак эрмитова сопряжения.
Если квантовая система описана с помощью матрицы плотности [1], то при переходе к классике у матрицы плотности пропадут недиагональные элементы 
и 
.
На физическом уровне кубит может быть представлен, например, как спин электрона, пользуясь его основным свойством – наличием только двух значений проекции спина, которые могут быть экспериментально измерены.
Пусть базисные состояния 
и 
представлены в виде двух векторов: 
и 
. Тогда для двух векторных бит в общем случае могут быть получены следующие 4 состояния, определяющие ортогональный базис: 
.
Например, при использовании этой формы записи одно из состояний формируется как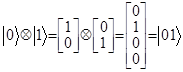 
.
Набор N кубитов составляет квантовый регистр. Регистр, в общем случае, также подчиняется принципу суперпозиции и находится одновременно во всех своих базовых классических состояниях, число которых 
. Произвольное состояние регистра записывается в виде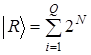 
. Общее состояние такой системы кубитов описывается тензорным произведением входящих в нее кубитов. Для матриц произведение Кронекера (тензорное) выполняется по правилу: 
.
Любая логическая операция с кубитами называется квантовым вентилем (преобразователем). По числу кубитов преобразователи делятся на одно- и многокубитные. Преобразователь переводит одно состояние регистра в другое. Физически реализуемые преобразователи соответствуют унитарным операциям с волновой функцией регистра. Из унитарности оператора следует его обратимость. Для демонстрации действия квантового преобразователя на кубиты используют матричную запись унитарного оператора [5].
В теории классических вычислений показано, что любую логическую операцию можно представить как совокупность базовых операций, например, парой NOT и XOR. Аналогично в квантовом случае: любую обратимую унитарную операцию можно представить, например, как один трехкубитный преобразователь Тоффоли (CCNOT) или Фредкина (CSWAP) или одно- и двухкубитный преобразователи (например, NOT и CNOT). Примеры квантовых преобразователей приведены в [2].
Однокубитные состояния могут быть выражены как векторы в пространстве, и в этом представлении 
есть пространственные вращения:
по оси x: 
, по оси y: 
, по оси z: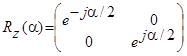 
.
Однокубитный преобразователь NOT
.
Действие преобразования Адамара (H) на каждый его вектор приводит к новому состоянию, которое фиксирует изменение положения вектора после преобразования:
.
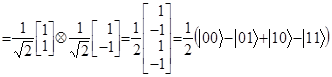Примерами двухкубитных преобразователей является преобразователи контролируемое НЕ (CNOT) и SWAP, который обеспечивает обмен содержимым между двумя кубитами. Введенные операторы позволяют создавать совокупность кубитов и преобразовывать их с помощью унитарных матриц.
Описание решения
Задание кубитов и визуализация матриц могут быть осуществлены в среде Matlab.
Явное задание первого кубита:
Q1=[1; 0]
Явное задание второго кубита:
Q2=[0; 1]
Визуализация матриц плотности двух кубитов (рис. 1, верхние левые графики):
RD1 =10 00; RD2 =0001
»subplot(1,2,1); bar3(RD1);
»subplot(1,2,2); bar3(RD2);
Применение преобразователя Адамара к обоим кубитам дает следующий результат
HQ1 =0.7071, 0.7071; HQ2 =0.7071, –0.7071
Визуализация результата (рис. 1, верхние правые графики)
RD1_H =0.5000, 0.5000, 0.5000, 0.5000
RD2_H =0.5000, –0.5000, –0.5000, 0.5000
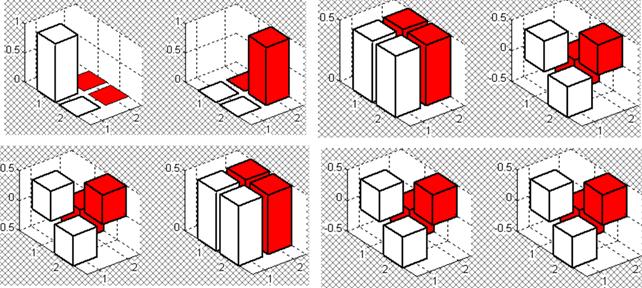
Рисунок 1. Визуализация матриц плотности двух кубитов (верхние левые графики); визуализация результата применение преобразователя Адамара к обоим кубитам (верхние правые графики); визуализация применения контролируемого обмена (нижние левые графики); визуализация применения контролируемого НЕ (нижние правые графики)
Применение контролируемого обмена с визуализацией результата (рис. 1, нижние левые графики)
RD1_H =0.5000, –0.5000, –0.5000, 0.5000
RD2_H =0.5000, 0.5000, 0.5000, 0.5000
»subplot(1,2,1); bar3(RD1_H);
»subplot(1,2,2); bar3(RD2_H);
Применение контролируемого НЕ с визуализацией результата (рис.1, нижние правые графики)
RD1_H =0.5000, –0.5000, –0.5000, 0.5000
RD2_H =0.5000, –0.5000, –0.5000, 0.5000
»subplot(1,2,1); bar3(RD1_H);
»subplot(1,2,2); bar3(RD2_H).
Особое место среди инструментальных приложений занимает система визуального моделирования SIMULINK. Разработка моделей средствами SIMULINK (s-моделей) основана на использовании технологии Drag-and-Drop.
Блоки, включаемые в создаваемую модель, могут быть связаны друг с другом как по информации, так и по управлению. Тип связи зависит от типа блока и от логики работы модели. Данные могут быть скалярными величинами, векторами или матрицами произвольной размерности. S-модель может иметь иерархическую структуру, число уровней иерархии практически неограниченно.
Представление преобразователя CNOT на рис. 2.
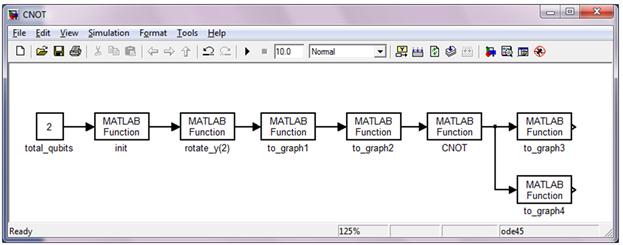
Рисунок 2. Преобразователь CNOT, реализованной в пакете Simulink
В блоке total_qubits вводится число кубитов, которое нужно создать. В блоке init формируется исходное состояние. Блок rotate_y(2) выполняет поворот второго кубита по оси y, для того чтобы преобразование CNOT можно было пронаблюдать.
Блоки to_Graph1, to_Graph2, to_Graph3 и to_Graph4 выполняют отображение состояния кубитов до и после преобразования. Блок CNOT выполняет контролируемое НЕ.
Пример работы модели показан на рис. 3. Первые два графика отображают исходные состояния кубитов, а третий и четвёртый – состояния после выполнения преобразования CNOT.
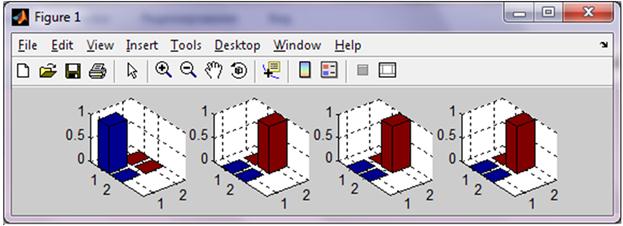
Рисунок 3. Преобразователь CNOT, реализованной в пакете Simulink
В данном случае второй кубит – контролирующий, поэтому с ним никаких изменений не произошло. Первый кубит – контролируемый, он изменил своё состояние.
Заключение
Разработан и апробирован подход моделирования операторов квантовых состояний в среде проектирования и моделирования Matlab и в его инструментальном пакете Simulink на примере работы двухкубитного преобразователя контролируемое НЕ (CNOT). Данный пример демонстрирует возможность применения сред Matlab/Simulink для проектирования систем, описываемых квантовыми состояниями.
Работа выполнена при поддержке Министерства образования и науки РФ в рамках Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России на 2009–2013 годы» (Государственный контракт № 14.B37.21.2021 от 11 ноября 2012 г).
Рецензенты:
Водяхо Александр Иванович, д.т.н., проф. кафедры вычислительной техники. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.
Пузанков Дмитрий Викторович, д.т.н., зав. кафедрой вычислительной техники. Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)», г. Санкт-Петербург.