Под интеллектуальными системами управления понимают системы, которые включают в контур управления вместе с подсистемами функционального управления подсистему логического управления, осуществляющую функцию логического выбора. В настоящей работе мы рассматриваем метод сетевого оператора [1–8], который используют для синтеза системы интеллектуального управления. Численный метод сетевого оператора позволяет с помощью генетического алгоритма найти структуру и параметры многомерной функции, представленной в форме целочисленной матрицы. Матрица сетевого оператора описывает граф сетевого оператора, который определяет аргументы и порядок выполнения вычислительных операций в многомерной функции.
Генетический алгоритм в методе сетевого оператора работает на множестве элементарных вариаций матрицы сетевого оператора [1; 2]. Особенность метода сетевого оператора для синтеза интеллектуальной системы управления заключается в том, что с помощью одного генетического алгоритм необходимо найти одновременно значение вектора параметров и две матрицы сетевого оператора. Первая матрица соответствует алгебраической многомерной функции, которая описывает функциональную подсистему управления. Вторая матрица соответствует логической функции, которая описывает подсистему управления логического выбора.
Решением задачи синтеза интеллектуальной системы управления является набор из трех элементов
![]() , (1)
, (1)
где ![]() – матрица функционального сетевого оператора размерностью
– матрица функционального сетевого оператора размерностью ![]() ,
, ![]() – матрица логического сетевого оператора размерностью
– матрица логического сетевого оператора размерностью ![]() ,
, ![]() – вектор параметров размерностью
– вектор параметров размерностью ![]() .
.
Для поиска структур матриц используем подход, основанный на принципе вариаций базисного решения. Определим следующие малые вариации матрицы сетевого оператора [4]:
0 – замена ненулевого недиагонального элемента ненулевым элементом;
1 – замена нулевого недиагонального элемента ненулевым элементом;
2 – замена ненулевого недиагонального элемента нулевым элементом;
3 – замена диагонального элемента.
Все перечисленные вариации могут описываться вектором из четырех элементов
![]() , (2)
, (2)
где ![]() – номер вариации,
– номер вариации, ![]() – номер строки матрицы,
– номер строки матрицы, ![]() – номер столбца матрицы,
– номер столбца матрицы, ![]() – номер унарной или бинарной операции.
– номер унарной или бинарной операции.
Все операции выполняются только при выполнении определенных условий. Например, вариация 0 матрицы выполняется, если элемент матрицы в строке ![]() и в столбце
и в столбце ![]() не равен нулю. Если условия выполнения вариаций не соблюдаются, то матрица не меняется.
не равен нулю. Если условия выполнения вариаций не соблюдаются, то матрица не меняется.
Согласно принципу базисного решения задаем базисные матрицы сетевых операторов
![]() ,
, ![]() , (3)
, (3)
![]() ,
, ![]() . (4)
. (4)
Для вариаций матрицы используем набор векторов вариаций
![]() , (5)
, (5)
где ![]() .
.
В результате действия набора векторов вариаций на матрицу получаем новую матрицу либо логического, либо функционального сетевого оператора. Для того чтобы определить какую именно матрицу, логического или функционального сетевого оператора, следует подвергать вариациям, используем дополнительный вектор-индикатор
![]() ,
, ![]() ,
, ![]() . (6)
. (6)
Если значение компоненты вектора-индикатора равно нулю, ![]() , то вариации, описываемой вектором вариаций
, то вариации, описываемой вектором вариаций ![]() , подвергается матрица сетевого оператора
, подвергается матрица сетевого оператора ![]() , если
, если ![]() , то – матрица логического сетевого оператора
, то – матрица логического сетевого оператора ![]() .
.
Новое возможное решение получаем из базисного ![]() с помощью множества векторов вариаций (6) на основании следующих соотношений:
с помощью множества векторов вариаций (6) на основании следующих соотношений:
![]() ,
, ![]() , (7)
, (7)
где
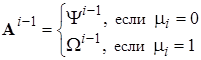 ,
, 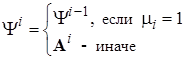 ,
, 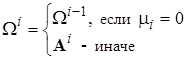 .
.
Любое возможное решение описывается конечным множеством векторов вариаций и закодированным кодом Грея вектором параметров. В качестве базисного решения используем две матрицы сетевого оператора, поэтому при использовании множества векторов вариаций для построения нового решения необходимо определить одну из двух базисных матриц сетевого оператора. Для этой цели используем вектор-индикатор базисного решения.
Рассмотрим пример построения нового возможного решения из базисных решений. Пусть имеем следующие базисные матрицы сетевого оператора
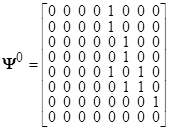 ,
, 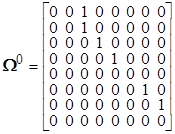 .
.
Пусть имеем следующее множество векторов вариаций
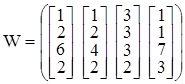 .
.
Пусть также имеем следующий вектор-индикатор
![]() .
.
Выполняем вариации согласно соотношению (11), получаем
![]() ,
, ![]() ,
,
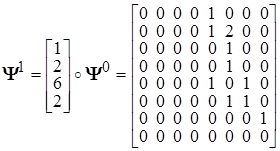 ,
,
![]() ,
, ![]() ,
,
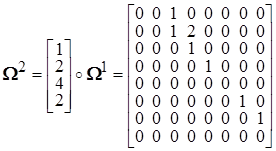 ,
,
![]() ,
, ![]() ,
,
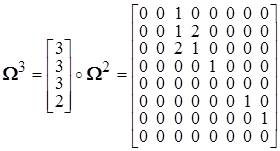 ,
,
![]() ,
, ![]() ,
,
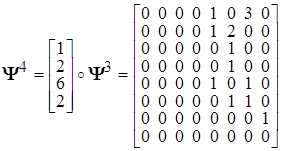 .
.
Для поиска значение вектора параметров используем традиционное представление вектора параметров в коде Грея
![]() ,
, ![]() ,
, ![]() , (8)
, (8)
где ![]() – размерность вектора параметров,
– размерность вектора параметров, ![]() – число бит под целую часть числа,
– число бит под целую часть числа, ![]() – число бит под дробную часть числа.
– число бит под дробную часть числа.
Вектор ![]() (8) представляет собой закодированный в виде кода Грея вектор параметров
(8) представляет собой закодированный в виде кода Грея вектор параметров ![]() . Преобразование из кода Грея в значение вектора параметров выполняется с помощью следующих соотношений
. Преобразование из кода Грея в значение вектора параметров выполняется с помощью следующих соотношений
![]() ,
, ![]() , (9)
, (9)
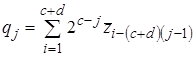 ,
, ![]() . (10)
. (10)
Рассмотрим подробнее генетический алгоритм многокритериальной оптимизации для решения задачи синтеза интеллектуальной системы управления.
Первоначально задаем базисное решение (5), которое включает базисные матрицы сетевых операторов ![]() ,
, ![]() и базисный вектор параметров
и базисный вектор параметров ![]() , который переводим в двоичный код Грея согласно соотношениям
, который переводим в двоичный код Грея согласно соотношениям
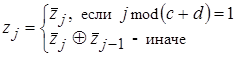 ,
, ![]() , (11)
, (11)
где ![]() – двоичный код вектора параметров
– двоичный код вектора параметров ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() – двоичный код компоненты
– двоичный код компоненты ![]() ,
, ![]() ,
, ![]() .
.
Создаем множество тождественных вариаций для базисного решения
![]() ,
,
где ![]() ,
, ![]() .
.
По условию принимаем, что нулевой вектор вариаций не меняет матрицу сетевого оператора. Задаем нулевой вектор-индикатор ![]() .
.
В результате получаем код базисного решения
![]() , (12)
, (12)
где ![]() – код Грея для вектора параметров
– код Грея для вектора параметров ![]() ,
, ![]() .
.
Генерируем множество кодов возможных решений
![]() ,
, ![]() , (13)
, (13)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Вычисляем для каждого возможного решения ![]() (11) значения функционалов
(11) значения функционалов
![]() . (14)
. (14)
Затем вычисляем для каждого возможного решения ![]() значение ранга
значение ранга
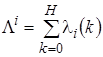 ,
, ![]() , (15)
, (15)
где
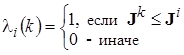 ,
, ![]() , (16)
, (16)
![]() , если
, если ![]() и
и ![]() ,
, ![]() .
.
При выполнении операции для двух случайно отобранных возможных решений
![]() ,
, ![]() (17)
(17)
определяем вероятность скрещивания решений ![]()
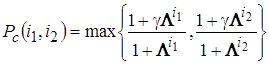 , (18)
, (18)
где ![]() – заданный параметр для вероятности скрещивания,
– заданный параметр для вероятности скрещивания, ![]() .
.
Параметр ![]() определяет нижнюю границу для вероятности скрещивания,
определяет нижнюю границу для вероятности скрещивания, ![]() . Максимальное значение ранга не может превосходить величину, равную количеству
. Максимальное значение ранга не может превосходить величину, равную количеству ![]() возможных решений, поэтому при больших рангах
возможных решений, поэтому при больших рангах ![]() и
и ![]() ,
, ![]() . Если
. Если ![]() или
или ![]() , то вероятность скрещивания равна единице
, то вероятность скрещивания равна единице ![]() .
.
Вычисляем случайную величину ![]() с помощью генератора случайных чисел. Если
с помощью генератора случайных чисел. Если ![]() , то возможные решения (16)
, то возможные решения (16) ![]() и
и ![]() скрещиваем.
скрещиваем.
При скрещивании выбираем случайно две точки скрещивания
![]() ,
, ![]() . (19)
. (19)
Строим четыре новых возможных решения
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
где
![]()
![]()
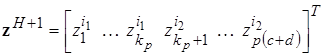 ,
,
![]()
![]()
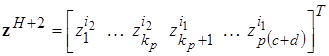 ,
,
![]()
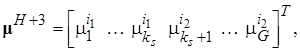
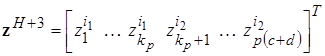 ,
,
![]()
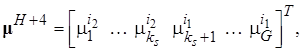
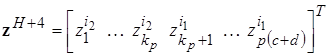 .
.
Выполняем возмущение каждого из решений. Данное возмущение обеспечивает случайный сдвиг решения относительно локального минимума и в генетическом алгоритме называется операцией мутации. Для выполнения операции мутации задаем в качестве исходных параметров алгоритма вероятность мутации
![]() . (24)
. (24)
Генерируем с помощью генератора случайных чисел случайную величину ![]() . Если величина
. Если величина ![]() , то выполняем операцию мутации.
, то выполняем операцию мутации.
Для выполнения операции мутации генерируем два случайных целых числа
![]() , (25)
, (25)
![]() , (26)
, (26)
Число ![]() определяет номер изменяемого элемента в структурной части возможного решения, а число
определяет номер изменяемого элемента в структурной части возможного решения, а число ![]() определяет номер изменяемого бита в параметрической части возможного решения.
определяет номер изменяемого бита в параметрической части возможного решения.
Если условие выполнения мутации ![]() удовлетворяется для одного из новых решений
удовлетворяется для одного из новых решений ![]()
![]() , то в нем генерируем новый вектор вариаций
, то в нем генерируем новый вектор вариаций ![]() , соответствующую компоненту
, соответствующую компоненту ![]() вектора-индикатора и компоненту
вектора-индикатора и компоненту ![]() кода Грея вектора параметров.
кода Грея вектора параметров.
После выполнения операции мутации для каждого нового возможного решения вычисляем значения функционалов
![]() ,
, ![]()
![]() . (27)
. (27)
Находим возможное решение с самым большим значением ранга ![]() ,
,
![]() . (28)
. (28)
Вычисляем ранг для первого нового решения
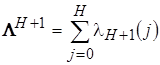 ,
, ![]() , (29)
, (29)
где
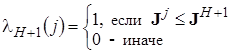 ,
, ![]() .
.
Если ранг первого нового решения меньше, чем наибольший ранг во множестве возможных решений, ![]() то заменяем возможное решение с наибольшим рангом на первое новое возможное решение
то заменяем возможное решение с наибольшим рангом на первое новое возможное решение
![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,. (30)
,. (30)
Пересчитываем ранги всех возможных решений по формуле (17) и находим возможное решение ![]() с наибольшим рангом (29). Вычисляем ранг второго нового возможного решения
с наибольшим рангом (29). Вычисляем ранг второго нового возможного решения
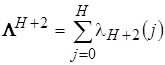 ,
, ![]() , (31)
, (31)
где
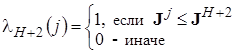 ,
, ![]() .
.
Если ранг первого нового решения меньше, чем наибольший ранг во множестве возможных решений, ![]() то заменяем возможное решение с наибольшим рангом на первое новое возможное решение
то заменяем возможное решение с наибольшим рангом на первое новое возможное решение
![]() :
: ![]() ,
, ![]() ,
, ![]() ,
, ![]() . (32)
. (32)
Повторяем те же действия для третьего и четвертого новых возможных решений ![]() ,
, ![]() .
.
После выполнения конечного числа операций отбора пар возможных решений для скрещивания завершаем вычисления.
Решением рассматриваемой задачи является множество Парето,
![]() . (33)
. (33)
Множество Парето составляют решения с нулевыми рангами
![]() ,
, ![]() . (34)
. (34)
Рецензенты:
Юрков Николай Кондратьевич д.т.н., профессор, заведующий кафедрой конструирования и производства радиоаппаратуры ФГОУ ВПО «Пензенский государственный университет», г. Пенза.
Никульчев Евгений Витальевич д.т.н., профессор, IT-директор по информационным технологиям ООО МАИК «Наука/Интерпериодика», г. Москва.
Бичурин Мирза Имамович, д.ф.-м.н., профессор, заведующий кафедрой проектирования и технологии радиоаппаратуры, Новгородский государственный университет, г. Великий Новгород.



