Введение
Разработка компьютерного симулятора робота с программным управлением призвана решить задачу тестирования и испытания создаваемой управляющей программы в виртуальной среде ПК до её запуска на реальной робототехнической системе. Это позволит избежать возможных сбоев или иных неприемлемых ситуаций, связанных с нештатным использованием технологического оборудования. Для решения этой задачи целесообразно использование средств ЭВМ совместно с искусственным интеллектом в виде систем продукционного типа [4; 7-8].
Цель
При создании системы компьютерной симуляции основной проблемой, возникающей перед разработчиком, является достижение соответствия виртуальных процессов, протекающих в симуляторе, их реальным аналогам, т.е. тем процессам, которые и необходимо симулировать в виртуальной среде. По этой причине симуляция робота в виртуальном пространстве с целью последующей интеллектуальной диагностики требует подходящей теоретической базы, формулирующей все необходимые данные о работе манипулятора.
Материал и методы
В качестве теоретической основы виртуализации целевой системы, рассмотрим обобщённую модель виртуального объекта управления, построенную по типу «вход-состояние-выход» (рис. 1).
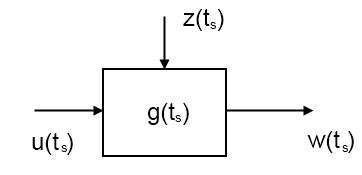
Рис. 1. Обобщённая модель виртуального объекта управления.
На рисунке 1 представлена модель виртуального объекта управления. Здесь u(ts) – виртуальные управляющие воздействия, z(ts) – виртуальные параметры окружающей среды, g(ts) – переменные состояния объекта управления, w(ts) – виртуальные выходные параметры. Аргумент ts выражает значение времени, причём индекс s означает, что время здесь является виртуальной (симулированной) величиной. Очевидно, что именно w(ts) является целевым вектором, получение которого и представляет собой решение задачи симуляции технической системы. Для того чтобы данные векторов w(ts) и g(ts) были максимально приближены к аналогичным данным, полученным на реальном объекте управления, величины векторов u(ts) и z(ts) также должны быть в как можно большей степени приближены к их реальным аналогам. В случае робота-манипулятора вектор u(ts) управляющих воздействий в большинстве случаев состоит из электрических сигналов системы управления, изменяющих состояние силовых приводов робота различного рода (электрических, гидравлических, пневматических или сервоприводов) [1; 5]. Кроме того, в состав этого вектора входят технологические параметры, также выраженные сигналами системы управления. Таким образом, симуляция входных сигналов не требует серьёзного теоретического фундамента для реализации в симуляторе. Вектор z(ts) содержит в себе т.н. возмущающие воздействия, т.е. все те параметры, которые не связаны с управляющим воздействием, однако тем не менее оказывают влияние на процессы, протекающие в объекте управления. Основным фактором окружающей среды, оказывающим возмущающее воздействие на перемещение манипулятора, является ускорение свободного падения [3]. Однако в большинстве случаев применяемые приводы роботов-манипуляторов имеют достаточную мощность, чтобы нивелировать влияние силы ускорения свободного падения в процессе перемещения [5]. По этой причине можно упростить поставленную задачу и отказаться от учёта силы ускорения свободного падения в создаваемой системе симуляции робота-манипулятора. Промежуточное положение между векторами управления u(ts) и выходных данных w(ts) занимает вектор переменных состояния g(ts). Этот вектор содержит в себе данные о перемещениях исполнительных органов манипулятора и режимах работы его подсистем. Данные о перемещении исполнительных органов в пространстве являются ключевыми сведениями о состоянии манипулятора и могут быть получены с использованием теоретических способов вычисления положений звеньев механизма.
Первоначально исследуем представление времени в компьютерных симуляторах. Симуляция, технической основой которой выступает ЭВМ, неизбежно ограничивается теми временными закономерностями, которые используются в самих вычислительных машинах. Речь идёт о дискретности течения времени в представлении ЭВМ. В связи с этим взамен реального непрерывного времени в симуляторе следует использовать такты, т.е., дискретные «скачки» времени, разделённые интервалами [9]. Введём зависимость (1), выражающую аргумент времени виртуального объекта управления.
![]() (1)
(1)
где ksоt – безразмерный коэффициент;
N – количество тактов симуляции;
T – время, прошедшее в реальном объекте управления.
Используя данную закономерность, можно получить выражение (2), формулирующее изменение положения звена с угловой степенью свободы, взяв за основу зависимость из [2].
![]() (2)
(2)
где ts – симулированное текущее значение времени;
ts.0 – симулированное начальное значение времени;
φ(t) – угол поворота звена в момент времени ts;
φ(ts.0) – угол поворота звена в начальный момент времени ts.0;
Ns – количество тактов симуляции, осуществлённых между начальным и текущим значениями симулированного времени;
ω – угловая скорость звена манипулятора.
Аналогично формулируются выражения для линейных перемещений звеньев. Таким образом, симулятор способен вычислять относительные положения звеньев манипулятора, т.е. данные вектора внутреннего состояния g(ts).
Теперь исследуем: как, используя значения вектора внутренних переменных, вычислить выходные данные виртуального объекта управления. Для решения этой задачи в робототехнике чаще всего используют метод однородных матричных преобразований, известный как метод Денавита-Хартенберга (ДХ-представление). Данный способ позволяет определить положение любого i-го звена манипулятора относительно системы координат любой j-й системы координат. В основе данного метода лежит единое расположение координатных осей для каждого из сочленений звеньев: ось zi направляется вдоль оси перемещения i-го звена, ось xi дополняет оси zi и zi-1 до правосторонней системы координат, ось yi дополняет оси zi и xi до правосторонней системы координат. ДХ-представление твёрдых звеньев зависит от четырёх геометрических параметров, соответствующих каждому звену. Эти четыре параметра полностью описывают любое вращательное или поступательное движение и определяются в соответствии с [5] следующим образом:
1) θi – присоединенный угол – угол, на который надо повернуть ось xi-1 вокруг оси zi-1, чтобы она стала сонаправлена с осью xi (знак определяется в соответствии с правилом правой руки);
2) di – расстояние между пересечением оси zi-1 с осью xi и началом (i-1)-й системы координат, отсчитываемое вдоль оси zi-1;
3) ai – линейное смещение – расстояние между пересечением оси zi-1 с осью xi и началом i-й системы координат, отсчитываемое вдоль оси xi, т.е. это кратчайшее расстояние между осями zi-1 и zi;
4) αi – угловое смещение – угол, на который надо повернуть ось zi-1 вокруг оси xi, чтобы она стала сонаправлена с осью zi (знак определяется в соответствии с правилом правой руки).
Для вращательных сочленений параметры di, ai и αi являются константами, а θi – изменяющейся величиной. С другой стороны, для поступательных сочленений θi, ai и αi – постоянные величины, а di – переменное значение. Значения θi для вращательного сочленения и di для поступательного называются обобщёнными координатами [5; 6].
Согласно ДХ-представлению, преобразование i-й системы координат к (i-1)-й, при заданных значениях θi, ai, αi, di, производится путём перемножения четырёх матриц однородных преобразований (3).
![]()
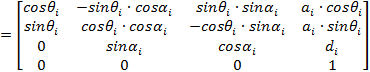 (3)
(3)
А положение i-й системы координат относительно j-й выражается матричным произведением (4):
![]() j < i. (4)
j < i. (4)
С точки зрения достаточного соответствия реально существующим промышленным манипуляционным системам [5], решено использовать в качестве манипулятора-прототипа плоский механизм с 6-ю степенями подвижности различных типов и одним неподвижным звеном (рис. 2).
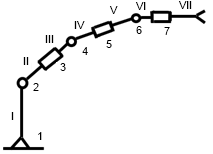
Рис. 2. Кинематическая компоновка манипулятора-прототипа. Арабскими цифрами обозначены сочленения, римскими – звенья механизма.
Результаты и их обсуждение
Для заданного манипулятора запишем значения матриц перехода Ai для двух различных кинематической пар: вращательной (А6) и поступательной (А7) соответственно.
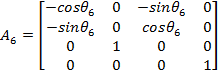
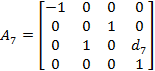
Аналогично, с некоторыми уточнениями, формулируются матрицы Ai для остальных сочленений звеньев.
Основная цель использования ДХ-преобразования – получение координат конечного звена манипулятора относительно базовой системы отсчёта. Эти данные необходимы для осуществления симуляции и интеллектуальной диагностики работы манипулятора. Запишем результирующее ДХ-преобразование в виде матрицы T70.
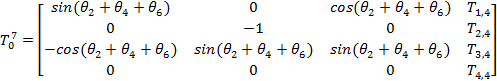
Для компактности записи элементы матрицы T70 под индексами T1,4, T2,4, T3,4, T4,4 будут представлены в виде отдельного вектора T1-4,4.
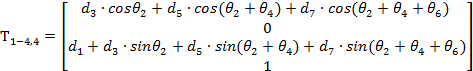
Отметим, что обобщённые координаты θi (угол поворота для вращательного сочленения) и di (перемещение для поступательного), очевидно, могут быть подменены симулированными значениями углового (2) и линейного перемещения. Таким образом, параметры вектора внутреннего состояния g(ts) используются для вычисления вектора выходных значений w(ts). Данные матриц ДХ-преобразований будут использованы в симуляторе для вычисления абсолютных координат манипулятора в виртуальном пространстве.
Заключение
Данные об изменении положений звеньев манипулятора в пространстве являются основными сведениями, необходимыми для анализа осуществляемой роботом деятельности и определения технологии, по которой работает робот. Эта информация является главной составляющей базы знаний интеллектуальной подсистемы, которая будет диагностировать поведение виртуального робота под программным управлением. Таким образом, получена теоретическая основа интеллектуальной диагностики работы виртуального робота.
Рецензенты:
Видовский Леонид Адольфович, д.т.н., доцент, профессор кафедры ВТиАСУ ФГБОУ ВПО «Кубанский государственный технологический университет», г. Краснодар.
Максименко Людвиг Александрович, д.т.н., профессор кафедры ВТиАСУ ФГБОУ ВПО «Кубанский государственный технологический университет», г. Краснодар.



