Предел прочности при статическом изгибе является одной из важнейших эксплуатационных характеристик слоистых композитных материалов, так как подавляющее число изделий из них испытывает в процессе эксплуатации деформацию статического изгиба и сжатия. При исследовании механических свойств прочностного характера фанеры с наполнителем в клеевом слое ставилась задача нахождения определенной математической модели рассматриваемого материала, основанной на результатах эксплуатационных исследований. Выбор модели позволяет получить объект, поведение которого под нагрузкой можно описать математическим уравнением.
Дифференциальное уравнение в частых производных для прямоугольной пластины, где в качестве переменных обычно берутся значения в прямоугольной системе координат (по Х, У), решается в рядах.
Расчет пластин с прямоугольным очертанием значительно более сложен, чем симметричных круглых пластин. Получается это, прежде всего, потому, что прогибы (перемещения) и напряжения несимметричных пластин определяются в функции не одного, а двух независимых переменных. Если пластина свободно опирается по четырем сторонам и находится под действием распределенной нагрузки q, то наибольший прогиб имеет место при Х=У=0, т.е.
![]() (1.1)
(1.1)
где ![]() – коэффициент, зависящий от отношения
– коэффициент, зависящий от отношения ![]() ;
;
![]() – меньшая сторона пластины;
– меньшая сторона пластины;
![]() – модуль упругости материала;
– модуль упругости материала;
![]() – толщина пластины;
– толщина пластины;
![]() – ширина пластины.
– ширина пластины.
Эта формула применима и к квадратной пластине со стороной ![]() .
.
При расчете за основной силовой фактор взята величина максимального внутреннего изгибающего момента для получения предела прочности и максимального касательного напряжения при разрушении. Наибольшие изгибающие моменты ![]() и
и ![]() из расчета на единицу длины сосредоточены в одной точке и определяются по формуле:
из расчета на единицу длины сосредоточены в одной точке и определяются по формуле:
![]() ,
, ![]() (1.2)
(1.2)
Коэффициенты ![]() ,
,![]() ,
,![]() для некоторых значений
для некоторых значений ![]() при
при ![]() приведены в таблице 1.
приведены в таблице 1.
Таблица 1 – значение коэффициентов ![]() ,
,![]() ,
,![]()
|
|
1,0 |
1,2 |
1,4 |
1,6 |
1,8 |
2 |
3 |
4 |
5 |
|
|
|
0,0433 |
0,0616 |
0,0770 |
0,0906 |
0,1017 |
0,1106 |
0,1336 |
0,140 |
0,1416 |
0,1422 |
|
|
0,0479 |
0,0626 |
0,0753 |
0,0862 |
0,0948 |
0,1017 |
0,1189 |
0,123 |
0,1246 |
0,1250 |
|
|
0,0479 |
0,0501 |
0,0506 |
0,0493 |
0,0479 |
0,0464 |
0,0404 |
0,0384 |
0,0375 |
0,0375 |
Если пластина защемлена по четырем краям, то наибольший прогиб имеет место по-прежнему в центре пластины (1.1).
Наибольший изгибающий момент возникает по серединам больших сторон, т.е. при ![]() и
и ![]() .
.
![]() (1.3)
(1.3)
Коэффициенты ![]() и
и ![]() для некоторых значений
для некоторых значений ![]() при
при ![]() приведены в таблице 2.
приведены в таблице 2.
Таблица 2 – значение коэффициентов ![]() и
и ![]()
|
|
1 |
1,25 |
1,50 |
1,75 |
2 |
|
|
|
0,0138 |
0,0199 |
0,0240 |
0,0264 |
0,0277 |
0,0284 |
|
|
0,0513 |
0,0665 |
0,0757 |
0,0817 |
0,0829 |
0,0838 |
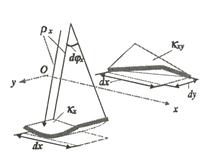
Рис. 1. Силовая схема линейного элемента во время деформации изгиба.
Пластина (пластинка) – тело призматической формы (рис. 1), высота которого ![]() мала в сравнении с наименьшим характерным размером
мала в сравнении с наименьшим характерным размером ![]() . Если отношение
. Если отношение![]() , но более
, но более ![]() , то пластина называется тонкой пластиной или просто пластиной. Если
, то пластина называется тонкой пластиной или просто пластиной. Если ![]() , то пластина называется мембранной. Наконец, если
, то пластина называется мембранной. Наконец, если![]() , то это уже плита. Наиболее практическое применение имеют слоистые пластины, которые и рассматриваются в настоящей статье, их расчет и испытание на статический изгиб. У тонких пластин
, то это уже плита. Наиболее практическое применение имеют слоистые пластины, которые и рассматриваются в настоящей статье, их расчет и испытание на статический изгиб. У тонких пластин ![]() . Плоскость, параллельная основаниям и делящая расстояние между ними пополам, называется срединной. Оси координат X и У будем располагать на срединной плоскости; перемещения вдоль осей X, У обозначим U, V. Ось Z показывает направление внешних, поперечных изгибающих нагрузок, а
. Плоскость, параллельная основаниям и делящая расстояние между ними пополам, называется срединной. Оси координат X и У будем располагать на срединной плоскости; перемещения вдоль осей X, У обозначим U, V. Ось Z показывает направление внешних, поперечных изгибающих нагрузок, а ![]() – направление прогиба пластины. Координатную систему считать будем неподвижной. В основе теории прогиба пластин лежат следующие гипотезы Кирхгофа:
– направление прогиба пластины. Координатную систему считать будем неподвижной. В основе теории прогиба пластин лежат следующие гипотезы Кирхгофа:
1) срединная плоскость пластины не деформируется, а только искривляется;
2) любой линейный элемент, перпендикулярный срединной плоскости, остается ей перпендикулярным и после изгиба, т.е. деформации, причем длина его не изменяется;
3) продольные слои пластины не давят друг на друга (![]() ).
).
Эти гипотезы очень близки к гипотезам, на которых основывается теория изгиба балок, поэтому напряжения в пластинках распределяются так же, как и в балках при изгибе (рис. 2).
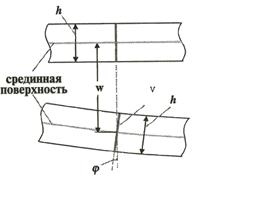
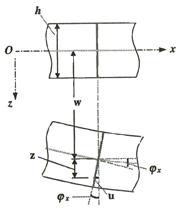
Рис. 2. Распределение напряжений в пластинке при изгибе.
![]() ;
; ![]() (1.4)
(1.4)
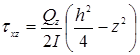 ;
; 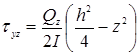 ,
,
где ![]() ;
; ![]() – нормальные напряжения;
– нормальные напряжения;
![]() ;
; ![]() – касательные напряжения в пластинах;
– касательные напряжения в пластинах;
![]() – изгибающие моменты и поперечные силы, отнесенные к единице длины пластины. Они определяются, если известна разрушающая функция прогиба
– изгибающие моменты и поперечные силы, отнесенные к единице длины пластины. Они определяются, если известна разрушающая функция прогиба ![]() из следующих зависимостей:
из следующих зависимостей:
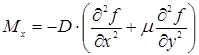 ;
; 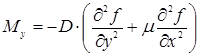
![]() ;
; 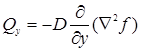 , (1.5)
, (1.5)
![]() где
где 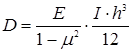 – цилиндрическая жесткость пластины,
– цилиндрическая жесткость пластины,
![]() – упругие постоянные материала пластины.
– упругие постоянные материала пластины.
Изгиб пластины сопровождается обычно её кручением с появлением крутящих моментов ![]() и вызываемых ими касательных напряжений
и вызываемых ими касательных напряжений ![]() (рис. 3).
(рис. 3).
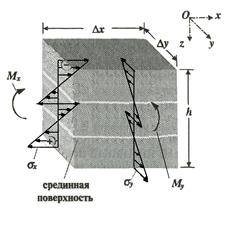
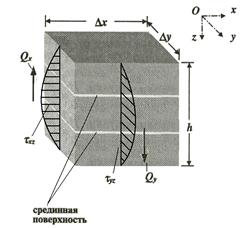
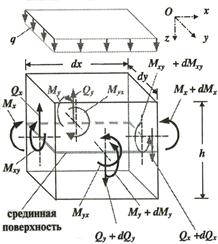
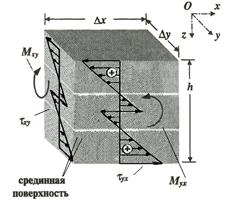
Рис. 3. Деформация в напряженной точке при изгибе пластины, характер изменения напряжений в точке и их эпюры.
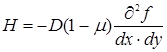 ;
; ![]() (1.6)
(1.6)
Для нахождения функции прогибов ![]() используют уравнение Софии – Жермен:
используют уравнение Софии – Жермен:
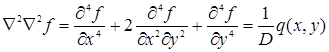 (1.7)
(1.7)
где ![]() – интенсивность распределенной по площади поперечной нагрузки на пластину.
– интенсивность распределенной по площади поперечной нагрузки на пластину.
При нахождении интеграла необходимо использовать граничные условия закрепления пластины (рис. 1).
Шарнирно – опорный край (грань СД): ![]() ;
; ![]() ;
;
Свободный край (грань ДА); ![]()
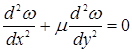 ;
;
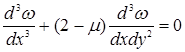 (1.8)
(1.8)
Математическая модель базировалась на основании статистических исследований слоистого композитного материала. При испытании на статический изгиб ставилась задача в определении предела прочности в зависимости от различных конструкционных особенностей материала. Для этого изменялись соотношения компонентов в клеевом слое и толщина клеевого слоя.
В процессе испытаний на гидравлической машине ГМС–50 создавались условия чистого изгиба в средней зоне согласно схеме, показанной на рис. 1. Скорость нагрузки принималась из расчета соблюдения условий кинетического подобия: -7000![]() 1500 Н/мин.
1500 Н/мин.
В результате испытаний получены статистические данные, приведенные в таблице 3. При нагружении образцов на статический изгиб некоторые из них вели себя как упругие, а некоторые как упруго-вязко-пластичные. Поэтому за основу модели слоистого композитного материала «Фенотрен» с наполнителем, как показали результаты анализа предела прочности при изгибе, принята упруго-вязко-пластичная модель тела.
Мгновенная упругая деформация слоистого материала происходила за счет деформации слоя древесины (шпона) и тонкого слоя наполнителя, где скорость изменения деформации соответствовала скорости изменения нагрузки при изгибе, т.е. наблюдалась линейная зависимость. Эластичная деформация, развивающаяся во времени, связана с вязким, все увеличивающимся сопротивлением аморфного слоя наполнителя и перемещением слоя древесины шпона относительного клеевого слоя слоистого материала. Относительные или простейшие деформации, выявленные в процессе испытания образцов, объединяясь, создают зону локальной пластической необратимой деформации, в которой в дальнейшем и наблюдается разрушение. Пластические деформации, так же как и упруго-вязкие, развиваются во времени.
Упругая и упруго-вязкая деформации намного превышают основную [5]. Исключение составляет лишь сжатие, особенно поперек волокон. В данной статье указанная модель применяется для объяснения вариантов перераспределения напряжений в образцах различной толщины (слоистости), как самого материала, так и клеевых слоев и шпона, возникающих вследствие больших градиентов напряжений в зонах поперечного сечения и жесткости слоев слоистого материала «Фенотрен».
Вывод: рассматривая виды (типы) разрушения образцов на статистический изгиб и анализируя статистические данные деформаций, следует заметить и принять, что процесс разрушения происходит фактически путем расслоения по клеевому слою с наполнителем при нагрузках, вызывающих упругие и упруго-пластичные деформации [1–4].
Рецензенты:
Ляпцев Сергей Андреевич, профессор, доктор технических наук, зав. кафедрой технической механики УГГУ, Уральский государственный горный университет, г. Екатеринбург.
Ковалев Р.Н., профессор, доктор технических наук, зав. кафедрой экономики транспорта и логистики УГЛТУ, Уральский государственный лесотехнический университет, г. Екатеринбург.



