Введение
Современное развитие ракетно-космической техники (РКТ) привело к необходимости поиска возможностей широкого применения ресурсосберегающих технологий на всех этапах ее жизненного цикла. На практике, в первую очередь, это проявляется в принятии новых ресурсосберегающих концепций эксплуатации РКТ, которые основаны на широком внедрении систем мониторинга ее технического состояния (ТС). Особое внимание при этом уделяется уникальным объектам РКТ длительного функционирования, к которым, например, относятся стартовые комплексы (СК) космического назначения.
В настоящее время существуют определенные трудности оценивания и прогнозирования ТС СК в процессе их эксплуатации. Причиной этого является отсутствие не только отработанного методического аппарата, но и отсутствие однородной статистической информации, необходимой для индивидуального прогноза изменения ТС как элементов СК (ЭСК), так и СК в целом. Поэтому традиционный статистический подход в прогнозировании ТС СК оказывается неприемлемым и возникает необходимость моделирования физических свойств таких систем и контроля физических параметров процессов их функционирования. Однако существующие СК не оборудованы средствами контроля, с помощью которых можно было бы отслеживать эволюцию деградационных свойств конструкционных материалов, накопление остаточных напряжений и деформаций элементов СК в процессе их эксплуатации. Это обусловлено, в частности, и тем, что ряд функционально важных элементов является практически недоступным для контроля. Например, на СК «Союз» к таким элементам относятся несущие стрелы, направляющие устройства, нижние кабель-мачты и их опорные узлы, гидродомкраты-тормоза и гидробуферы. Детальное обследование последних невозможно без их демонтажа и дальнейшей разборки.
В связи с этим возникает необходимость решения следующих актуальных задач:
- разработка моделей ТС ЭСК, учитывающих влияние деградационных процессов, и методов их использования при разработке системы оценивания и прогнозирования ТС ЭСК и методов извлечения знаний из разнородных данных, получаемых в процессе эксплуатации СК;
- разработка рекомендаций для создания средств контроля ТС СК при их функционировании.
Целью настоящей статьи является изложение результатов научных исследований, выполненных авторами и направленных на решение первой из перечисленных задач на основе использования методов искусственного интеллекта.
Постановка задачи синтеза модели оценивания и прогнозирования ТС СК
Будем предполагать, что исходная информация для построения дискриминантных моделей состояний имеет вид таблицы экспериментальных (эксплуатационных) данных, в которой признаки могут быть измерены в логической, номинальной или числовой шкале, а также в шкале линейного порядка [6].
Введем обозначения:
О – ЭСК, для которого строится дискриминантная модель ТС;
X= 
– вектор-столбец параметров ЭСК, информация о которых доступна;
I=
– множество индексов номеров компонент вектора признаков, 
;
– подвектор вектора признаков, состоящий из тех его компонент, номера, которых входят в индексное множество 
;
C=<
> – нормированный вектор-столбец стоимостей измерений компонент вектора X;
Q={
} – множество классов ТС ЭСК , где k – общее число классов состояний;
N – суммарное число строк таблицы обучающих данных, 
– число строк таблицы, которые относятся к классам состояний 
, s=1,2,...,k;
M(О)={M(
M
,...,M(
)} дискриминантная модель ЭСК ,
M={M
(О)}
– множество возможных дискриминантных моделей состояний ЭСК с именем О,
DR={
}, gÎ{1,2,...,G} – множество возможных методов принятия решений.
Содержательно задача синтеза дискриминантной модели ЭСК формулируется следующим образом.
Дано: множество классов состояний Q ЭСК; пространство признаков X и вектор стоимости измерений его параметров C; множество возможных дискриминантных моделей M; множество правил принятия решений DR; пороговое значение вероятности правильной классификации состояния 
; ограничение снизу на вероятность правильного распознавания класса состояний ЭСК 
,( j=1,2,...,k).
Найти: дискриминантную модель M(О)={M( M,...,M()}ÎM, для которой существует метод принятия решений Î DR, обеспечивающий возможность классификации состояний ЭСК с заданным уровнем вероятности правильной классификации, которая требует состава измерений минимальной стоимости
при ограничениях 
.
На практике множество возможных ТС ЭСК может включать в себя достаточно много классов. Если в этом случае пытаться строить схему принятия решений таким образом, чтобы сразу за один шаг по результатам измерений параметров объекта оценить класс состояний, то такая схема может оказаться очень сложной и неэффективной.
Чтобы ослабить сложность этих проблем, обычно используется подход, в котором на каждом шаге делается выбор только из двух альтернатив, и тогда процесс принятия решений сводится к последовательности из нескольких более простых шагов. Кроме того, объем знаний, который используется при этом на каждом шаге, тоже оказывается существенно меньшим, а потому процедуры вывода становятся тоже намного проще. Такой подход принято называть подходом на основе дерева решений. Дерево решений называют еще метасхемой принятия решений [4].
Продемонстрируем идею использования метасхемы на примере. Рассмотрим следующее множество классов ТС ЭСК:
- ЭСК исправен и работоспособен;
- ЭСК неисправен, но работоспособен;
- ЭСК неработоспособен, но его работоспособность может быть восстановлена при выполнении ремонтно-профилактических работ силами эксплуатационного персонала;
- ЭСК неработоспособен, его работоспособность может быть восстановлена только с большими финансовыми затратами;
- ЭСК работоспособен, но его дальнейшая эксплуатация нецелесообразна из-за больших эксплуатационных затрат;
- ЭСК работоспособен, но его дальнейшая эксплуатация нецелесообразна из-за низкой надежности (комплект достиг предельного состояния по критериям безопасности);
- работоспособный ЭСК находится в предотказном состоянии.
Обозначим классы ТС, введенные в этом примере, символами q1, q2, ...,q7, присваивая им эти имена в порядке перечисления состояний. Поставим в соответствие этим классам состояний пропозициональные переменные с теми же именами, и будем полагать, что они принимают значение "истина", когда ТС отвечает соответствующему классу, и значение "ложь", когда это не так. Заметим, что в каждом конкретном случае истинной может быть только одна пропозициональная переменная из этого списка.
Введем следующие метаклассы состояний, каждый из которых определяется некоторой логической формулой над пропозициональными переменными q1, q2, ...,q7:
mq0=q1Úq2Úq3Úq4Úq5Úq6Úq7, mq1=q1Úq2Úq3Úq4Úq5, mq2= q6Úq7,
mq3=q1Úq2, mq4=q3Úq4Úq5, mq5=q3Úq4.
Запишем определения введенных метаклассов, используя эти обозначения:
mq0=mq1Úmq2, mq1= mq3Ú mq4, mq2= q6Úq7, mq3=q1Úq2, mq4= mq5Úq5, mq5=q3Úq4.
Отношение порядка на множестве введенных метаклассов и исходных классов состояний представлено на рис.1.
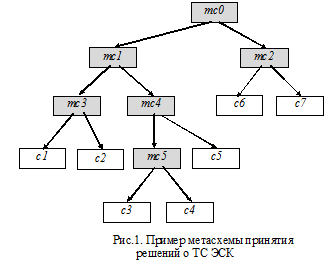
Различение двух классов – задача значительно более простая, чем, например, различение семи классов.
Следующий шаг, который необходимо сделать на пути решения задачи синтеза модели оценивания и прогнозирования ТС ЭСК после построения метасхемы классов ТС, связан с отбором информативных признаков.
Алгоритм оптимального выбора информативных признаков
Рассмотрим формальную постановку задачи и алгоритм оптимального выбора наиболее информативных подпространств признаков, характеризующих ТС СК. Пусть, как и ранее, 
– вектор признаков ТС СК; Q={0,1} – пара альтернативных классов ТС СК, 
– подмножество множества компонент вектора признаков X, 
мера информативности набора признаков 
, в качестве которой выберем расстояние между классами ТС СК, обладающее свойством аддитивности [7].
Помимо меры информативности, которая характеризует свойства подпространства признаков по способности различения пары классов состояний, важным свойством набора признаков является стоимость получения информации об их значениях. Будем полагать, что эта стоимость вычисляется по формуле
где 
– стоимость набора признаков 
, 
– стоимость получения информации о признаке 
.
Необходимо при известных X и найти
при условии
С(Хl) £ СД,
где R(Хl)= (а0,1 N0 N1 )-1 {
}1/2 ;а0,1 – нормирующий множитель; N0, N1 – общее число реализаций в кластерах “0” и “1” соответственно; А – симметричная матрица весовых положительных коэффициентов.
Для ее решения воспользуемся методом динамического программирования [1].
Функциональные уравнения Беллмана для прямого хода алгоритма динамического программирования имеют вид:
для первого шага
для 
, 
для 
;
для второго и последующих шагов
, 
, 
,
где 
– возможное значение располагаемых ресурсов для каждого шага алгоритма;
– условно оптимальное значение i- го признака для данного значения 
.
Оптимальный набор признаков, характеризующий ТС СК с максимальной информативностью, и суммарная стоимость получения (измерения) которых не превышает допустимую, определяется в результате обратного хода с использованием формул:
, 
, 
,
где 
– оптимальное значение i - го признака.
Как было отмечено выше, эти признаки являются результатами измерений, представленными в различных шкалах. Для обнаружения закономерностей, характеризующих деградационные процессы в ЭСК, необходимо их приведение к единой шкале. Существующие способы сведения числовой шкалы к логической основаны на замене данных числовой шкалы утверждениями об их принадлежности тому или иному интервалу этой шкалы. Такой подход в данном случае не применим, так как и без того огромное количество признаков, характеризующих состояние ЭСК, становится катастрофически большим, что сильно затрудняет решение задачи обучения интеллектуальной системы оценивания и прогнозирования.
Для решения этой проблемы предлагается новый подход к приведению данных, измеренных в числовой шкале или шкале порядка, к бинарной шкале. Он основан на построении разделяющих гиперплоскостей между кластерами обучающих данных и вычислении значений предиката, характеризующего принадлежность вектора признаков состояния одному из классов, для каждого информативного подпространства, найденного при решении задачи оптимального выбора информативных признаков. Рассмотрим сущность этого подхода.
Преобразование разнотипных данных к единой шкале
В соответствии с идеей, высказанной в работе [8], распространим возможности разделяющих правил на задачу преобразования данных, представленных в числовой шкале, к логической форме описания.
Пусть найдено подмножество информативных подпространств 
, где каждое подпространство 
характеризуется подмножеством признаков 
размерности 1, 2 или 3, и в множестве P они упорядочены по мере информативности. Рассмотрим произвольное подпространство , и в нем одним из известных способов [2], [3], [5] построим линейную разделяющую границу между двумя кластерами обучающих данных, которая в одномерном подпространстве будет иметь вид просто числа, в двухмерном случае – вид прямой линии, а в трехмерном случае – вид плоскости. Будем полагать, что эта линейная разделяющая граница делит все множество представителей обучающих данных классов 0 и 1 таким образом, что "в основном" представители одного класса находятся по одну сторону линейной разделяющей границы, а представители другого класса – по другую ее сторону.
Уравнение этой линейной разделяющей границы имеет вид
L
X
+b
= 0
где L – транспонированный вектор коэффициентов линейной формы, b
– свободный член уравнения “разделяющей” гиперплоскости, X – вектор признаков подпространства П. При этом решающее правило в обычном для теории классификации смысле [285] имеет вид:
если LX+b³ 0, то X ϵ классу 1, если LX+b< 0, то X ϵ классу 0.
Это правило может быть представлено в виде предиката если P(LX+b
, который обозначим символом Pj. С учетом этого обозначения решающее правило примет вид
если Pj =”true”, то X ϵ классу1, если Pj =”false”, то X ϵ 0.
Таким образом, в таблице экспериментальных данных вместо подпространства непрерывных признаков, отвечающих подвектору X, появится новый признак Pj , который описывается уже в логической шкале.
Заметим, что точно таким же образом можно преобразовать к бинарной шкале и признаки, измеренные в шкале порядка.
Заключение
Разработка системы оценивания и прогнозирования ТС ЭСК включает в себя в качестве первой и важнейшей задачи разработку формальной модели, отражающей основные закономерности, свойственные каждому из состояний ЭСК. В результате проведенных исследований математически сформулирована общая задача синтеза интеллектуальной модели такой системы и разработаны предложения по ее решению. К их числу относятся математическая модель и метод решения задачи определения оптимального набора информативных признаков, необходимых для оценивания и прогнозирования ТС ЭСК, и новый подход к приведению данных, измеренных в числовой шкале или шкале порядка, к бинарной шкале, что позволяет решить задачу извлечения знаний из набора разнотипных данных. Полученные результаты могут быть положены в основу построения замкнутой интеллектуальной системы управления ТС СК и других объектов космического назначения.
Рецензенты:
Петров Геннадий Дмитриевич, доктор технических наук, профессор, начальник кафедры, ВКА имени А. Ф.Можайского, г. Санкт-Петербург.
Кулешов Юрий Владимирович, доктор технических наук, профессор, начальник кафедры, ВКА имени А. Ф.Можайского, г. Санкт-Петербург.