Введение
Решение проблемы увеличения пропускной способности интерфейсов передачи данных, входящих в состав информационно-измерительных и управляющих систем (ИИУС) за счет сжатия информации и увеличения скорости её передачи относится к числу актуальных. Наиболее эффективными путями решения проблемы являются разработка алгоритмов сжатия-восстановления информации и их программная реализация.
Цель исследования
Выбор программного обеспечения должен производиться исходя из требований, предъявляемых к конкретной ИИУС, поэтому разработчикам необходимо наличие информации о характеристиках алгоритмов.
Целью представленной работы является сравнение метрологических характеристик и функциональных возможностей трех алгоритмов сжатия информации на основе метода Прони.
Материал и методы исследования
В настоящее время известен ряд методов сжатия-восстановления информации, среди которых выделяется метод Прони, позволяющий восстанавливать сигнал не только по авторегрессионным коэффициентам, но и по параметрам разложения [2].
Для упрощения реализации метода Прони могут использоваться методы разложения сигнала на колебательные и затухающие составляющие, такие как метод декомпозиции на эмпирические моды (Empirical Mode Decomposition) и метод на основе экстремальной фильтрации (Extreme Filtration).
Метод разложения на эмпирические моды и метод на основе экстремальной фильтрации схожи по сути и позволяют получать разложение на те же составляющие, что и метод Прони, не требующий выполнения сложных вычислительных процедур, такой, например, как решение степенного уравнения.
Метод декомпозиции на эмпирические моды является одним из современных в области цифровой обработки сигналов, подходит для анализа нелинейных и нестационарных сигналов вследствие высокой степени адаптации к сигналам, следовательно, данный метод отражает реальное поведение сигналов. Особенностью метода является возможность разложения сигнала на конечное число «эмпирических мод», каждая из которых содержит определенную информацию об исследуемом процессе [6]. Моды являются функциями, не имеющими строгой аналитической записи, однако удовлетворяющими двум необходимым условиям:
1) общее число экстремумов равняется общему числу нулей с точностью до 1;
2) полусумма верхней огибающей, интерполирующей локальные максимумы, и нижней огибающей, интерполирующей локальные минимумы, близка к нулю. В качестве способа интерполяции почти всегда используются кубические сплайны, что объясняется их высокой гладкостью. В отличие от гармонического сигнала, где модель сигнала задаётся заранее, эмпирические моды вычисляются в ходе процесса, что и подчеркивается в названии метода (эмпирические моды-функции, извлеченные непосредственно из реального сигнала).
Метод на основе экстремальной фильтрации (Extreme Filtration) позволяет исследовать сигналы сложной формы, например, сумму нескольких гармонических колебаний, или переходные процессы. Особенностью алгоритма является то, что для анализа используются только экстремумы сигнала [5]. Этот факт также может быть положен в основу концепции сжатого хранения данных – при этом еще при регистрации сигнала можно фиксировать только его экстремумы и, таким образом, изначально сократить количество обрабатываемой информации. Экстремумы используются в дальнейшем для аппроксимации гауссовыми кривыми. Процедура аппроксимации связана с выделением из сигнала знакопеременных составляющих, каждая из которых может быть отнесена к определенной полосе частот. Таким образом, гауссовскими функциями описывается каждый из экстремумов определенной частотной составляющей сигнала.
Итак, алгоритм разложения на основе этого метода должен включать следующие процедуры:
1) выделение из сигнала экстремумов – данная процедура, проделанная с исходным сигналом, в дальнейшем повторяется над сглаженными последовательностями, отфильтрованными с помощью цифрового фильтра;
2) фильтрация – данная процедура выделяет очередную высокочастотную по сравнению с оставшимися в последовательности составляющую;
3) собственно аппроксимация каждой из выделенных по экстремумам частотных составляющих сигнала базисными функциями.
Алгоритмы, реализующие варианты совместного применения методов разложения сигнала на колебательные и затухающие составляющие и метода Прони, позволяют решить некоторые проблемы, возникающие при применении традиционного метода Прони:
- уменьшается критичность результата анализа к порядку модели;
- уменьшается трудоемкость вычислений параметров составляющих (для каждой моды этот процесс сводится к решению квадратных или кубических уравнений);
- появляется возможность фильтрации сигнала еще до применения метода Прони [1].
Вариант совместного использования метода декомпозиции на эмпирические моды (EMD + Прони) и метода Прони отличается от традиционного применением алгоритма Прони не к исходному сигналу, а к выделенной в процессе декомпозиции моде.
Вариант совместного использования алгоритма на основе экстремальной фильтрации и алгоритма Прони (EF+Прони) заключается в применении алгоритма Прони к каждой выделенной высокочастотной составляющей.
Для оценки предложенных алгоритмов следует рассмотреть их функциональные и метрологические характеристики. При сертификации процедуры сжатия-восстановления к функциональным характеристикам следует отнести объем входной информации и коэффициент сжатия, к метрологическим – погрешность восстановления сигнала и время выполнения процедуры [1].
Наиболее достоверной оценкой погрешности восстановления является среднеквадратическое отклонение отсчетов исходного ряда от аппроксимирующей функции, приведённое к пределу измерения сигнала 
:
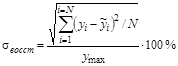, (1)
где 
– значения отсчетов аппроксимирующей функции в i-й точке, 
– количество отсчётов.
Сравнительная оценка характеристик алгоритмов Прони, EMD + Прони и EF +Прони при решении задачи сжатия-восстановления проводилась в относительных единицах в среде MatLab при объеме информации N от 100 до 30000 результатов измерения.
При исследовании применялась следующая дискретная модель измерительного сигнала:
, 
, (2)
где 
, 
, 
– амплитуда, частота и фаза m-й гармоники сигнала, соответственно; i – номер отсчета сигнала (дискретное время); 
– значения аддитивного белого шума с нулевым матожиданием и дисперсией 
в моменты отсчетов; q – отношение сигнал/шум; N – количество зарегистрированных дискретных отсчетов (результатов измерений); 
– шаг дискретизации, согласно теореме Котельникова определяемый соотношением:
, (3)
где 
– максимальная частота, n – число периодов сигнала за время измерения.
Для моделирования квантования уровня сигнала в процессе аналого-цифрового преобразования модель (2) была дополнена следующим образом [3]:
, (4)
где d – количество разрядов АЦП с двоичным шагом квантования; 
– ближайшее целое числа x.
С помощью функции 
учитываются шумы квантования АЦП при условии, что значение амплитуды 
измеряемого сигнала 
не выходит за пределы рабочего диапазона АЦП. Модель (4) позволяет формировать сигнал любой сложности, в частности, при проведении исследования погрешности восстановления была принята модель в виде суммы трех гармоник [4].
Результаты исследования
По результатам моделирования алгоритмов в среде MatLab установлено, что наилучшие показатели функциональных возможностей имеет алгоритм Прони с предварительным применением метода на основе экстремальной фильтрации, однако алгоритм Прони с предварительным разложением на эмпирические моды также имеет высокие показатели, поэтому необходимо проанализировать метрологические характеристики этих двух методов.
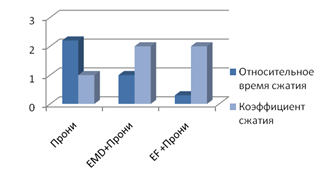
Рис. 1. Характеристики процедуры сжатия-восстановления методами Прони, EMD + Прони, EF+Прони.
В результате исследований были получены оценки погрешности восстановления δ результатов измерений в зависимости от объема информации N (рис. 2) и значения коэффициентов сжатия для методов Прони с предварительным разложением на эмпирические моды и применением метода на основе экстремальной фильтрации. В диапазоне от 100 до 3000 отсчетов сигнала коэффициент сжатия двух исследуемых алгоритмов возрастает пропорционально увеличению числа отсчетов 
, где знаменатель определяется произведением трех извлеченных мод на четыре параметра моды/высокочастотной составляющей, найденных по методу Прони.
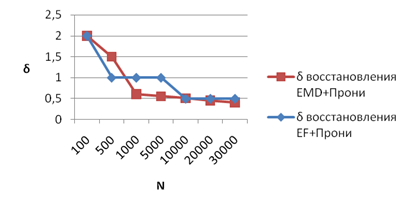
Рис. 2. Зависимость погрешности восстановления сигнала δ от объема информации N при использовании алгоритмов EMD+Прони и EF +Прони.
Оценка времени выполнения алгоритма зависит от аппаратной реализации, выбранной пользователем, вследствие чего указание времени, затраченного на выполнение алгоритма при моделировании метода в среде MatLab, является некорректным.
Заключение
1. Алгоритмы сжатия измерительных сигналов на основе метода Прони с предварительным разложением на эмпирические моды и предварительным применением метода на основе экстремальной фильтрации обладают более высокими функциональными и метрологическими характеристиками (коэффициент сжатия, погрешность восстановления), чем алгоритм с применением традиционного метода Прони. Оба метода могут использоваться в различных ИИУС, в зависимости от предъявляемых требований, метод Прони с предварительным применением алгоритма на основе экстремальной фильтрации может найти широкое применение в системах, основным требованием которых является быстродействие.
2. В результате проведенного моделирования было выяснено, что коэффициент сжатия сигнала при применении модифицированных методов на основе Прони (EMD+Прони и EF+Прони) прямо пропорционален объему информации в диапазоне от 100 до 30000 результатов измерений с коэффициентом пропорциональности 1/12. Погрешность восстановления, обусловленная применением предложенных алгоритмов, не превышает ±0,5%.
Рецензенты:
Трофимов Алексей Анатольевич, д.т.н., доцент, заместитель начальника учебно-научного центра ОАО «НИИФИ», г. Пенза.
Нефедьев Дмитрий Иванович, д.т.н., профессор, зав. кафедрой «Информационно-измерительная техника» ФГБОУ ВПО «Пензенский государственный университет», г. Пенза.