Введение
На современном этапе очень актуальна проблема кадрового воспроизводства научного и научно-педагогического заведений высшего профессионального образования. В связи с этим появилась необходимость в разработке и апробации методики и моделей для прогнозирования динамики кадров высшей научной квалификации.
В настоящей статье предлагается математическая модель для прогнозирования численности претендентов на поступление в аспирантуру среди учащихся заведений высшего профессионального образования в виде системы обыкновенных дифференциальных уравнений с отклоняющимся аргументом [5], широко использующихся для моделирования динамики социально-экономических процессов [2]. Эта задача ставится в рамках решения более общей задачи прогнозирования потока научных и научно-педагогических кадров [4]. В основу построения модели положены механизмы, использующиеся для прогнозирования социодемографического поведения населения [1]. На основе разработанного численного алгоритма и с использованием статистических данных об успеваемости студентов очной формы обучения специальности «Прикладная математика и информатика» математического факультета МГУ им. Н.П. Огарева за промежуток времени, предшествующий прогнозируемому, находятся неизвестные параметры математической модели.
Постановка задачи
Рассмотрим процесс обучения студентов с момента поступления до окончания высшего учебного заведения. Множество студентов, поступивших в университет в 
-м году будем называть -м потоком студентов. Очевидно, что каждый поток студентов, достигая фиксированной сессии, оказывается в похожих обстоятельствах, так как набор преподавателей и сложность изучаемых предметов в соответствующих семестрах зачастую остаются неизменными. А значит, влияние данных факторов на численные значения потоков, вливающихся в группу претендентов на поступление в аспирантуру (и выбывающих из нее), можно оценить по статистической информации о данных показателях за некоторый отрезок времени, предшествующий прогнозируемому, и по количественному составу этой группы в данный момент времени. Всё множество студентов разобьем на две группы: группу претендентов на поступление в аспирантуру и группу остальных студентов. Сделать это можно, например, взяв за критерий некую фиксированную величину среднего балла на последних экзаменах. Состав группы претендентов на поступление в аспирантуру будет меняться два раза в год по итогам очередной сессии. Часть студентов будет выбывать из данной группы, а часть – в нее вливаться.
Предположим, что изменение потока присоединяющихся к группе претендентов на поступление в аспирантуру в фиксированный момент времени зависит от численности претендентов на поступление в аспирантуру по результатам предыдущей сессии, от потока присоединяющихся к группе претендентов на поступление в аспирантуру и от потока выбывающих из группы претендентов на поступление в аспирантуру на аналогичном этапе обучения предыдущего потока. С учетом вышеперечисленных предположений математическая модель, описывающая динамику потока присоединяющихся к претендентам на поступление в аспирантуру для -го потока студентов описывается дифференциальным уравнением с отклоняющимся аргументом следующего вида:
,
где 
– численность претендентов на поступление в аспирантуру в момент времени 
; 
– численность потока присоединяющихся к группе претендентов на поступление в аспирантуру в момент времени ; 
– численность потока выбывающих из группы претендентов на поступление в аспирантуру в момент времени ; 
– длительность семестра; 
– кусочно-постоянные функции, зависящие от времени .
Аналогичным образом предположим, что изменение потока выбывающих из группы претендентов на поступление в аспирантуру в фиксированный момент времени зависит от численности претендентов на поступление в аспирантуру по результатам предыдущей сессии, потока выбывающих из группы претендентов на поступление в аспирантуру и потока присоединяющихся к группе претендентов на поступление на аналогичном этапе обучения предыдущего потока. Таким образом, изменение потока выбывающих из группы претендентов на поступление в аспирантуру в момент времени описывается дифференциальным уравнением с отклоняющимся аргументом следующего вида:
.
Балансовое уравнение, связывающее прирост и отток численности претендентов на поступление в аспирантуру с количеством людей в данной группе, имеет вид:
,
Итоговая модель, описывающая динамику численности претендентов на поступление в аспирантуру, может быть записана в виде следующей системы дифференциальных уравнений с отклоняющимся аргументом:
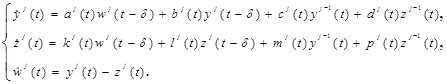(1)
Ставится задача отыскания неизвестных кусочно-постоянных параметров 
, зависящих от времени , на основе известных статистических данных о значениях функций 
за предшествующий период времени.
Для решения поставленной задачи в статье предлагается численный алгоритм нахождения неизвестных параметров системы (1).
Построение разностной вычислительной схемы
Перейдем от системы дифференциальных уравнений к разностной вычислительной схеме, позволяющей найти неизвестные параметры модели. Заметим, что в системе (1) используются «мгновенные» значения численности претендентов на поступление в аспирантуру потоков, вливающихся в эту группу и выбывающих из нее. На практике статистические данные о численности претендентов на поступление в аспирантуру могут быть получены лишь за определенный промежуток времени. В силу этого применим к системе (1) интегро-интерполяционный метод построения разностных схем [3].
Для построения разностной схемы на отрезке 
введем равномерную сетку с шагом 
, то есть множество точек 
, 
, 
, таким образом, чтобы 
, где 
Проинтегрировав систему (1) по отрезку 
, предполагая, что коэффициенты 
на 
-м отрезке постоянны и не зависят от времени (обозначим их за 
), получим систему:
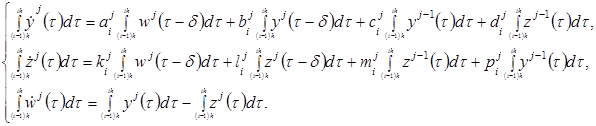, (2)
Введем следующие обозначения 
, 
, 
. Тогда 
, 
, 
.
Следовательно, 
и 
.
Аппроксимируем конечными разностями 
, 
, 
– соответствующие интегралы от производных в левых частях системы (2). С учетом этих замечаний получим следующую систему конечно-разностных уравнений:
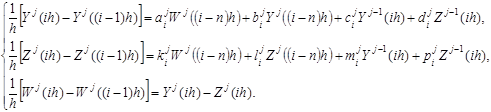(3)
Вводя для краткости записи системы (3) для -го отрезка временной оси и 
-го потока следующие обозначения:
, 
, 
,
запишем систему уравнений:
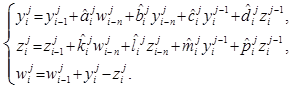(4)
Здесь 
– количество студентов -го потока, присоединяющихся к группе претендентов на поступление в аспирантуру в момент времени 
, 
– количество студентов -го потока, выбывающих из группы претендентов на поступление в аспирантуру в момент времени , 
– численность группы претендентов на поступление в аспирантуру -го потока студентов в интервале времени 
Описание численного алгоритма решения разностной схемы
Для экспериментальной проверки системы уравнений (4) шаг сетки 
выбирается равным промежутку времени между фиксированными учетами успеваемости студентов. Если учёт успеваемости проводится только один раз за семестр, то – шаг сетки – равен продолжительности семестра , и в системе (4) 
. В этом случае система уравнений (4) примет вид:
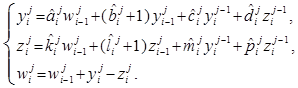(5)
Здесь – количество студентов -го потока, присоединяющихся к группе претендентов на поступление в аспирантуру после -й сессии, – количество студентов -го потока, выбывающих из группы претендентов на поступление в аспирантуру после -й сессии, – численность группы претендентов на поступление в аспирантуру -го потока студентов после -й сессии.
Изложим численный алгоритм нахождения неизвестных параметров системы (5) на примере учащихся заведений высшего профессионального образования. Схематически зависимость и 
от значений функций 
предыдущих сессий и потоков в системе (5) представлена на рисунке 1.
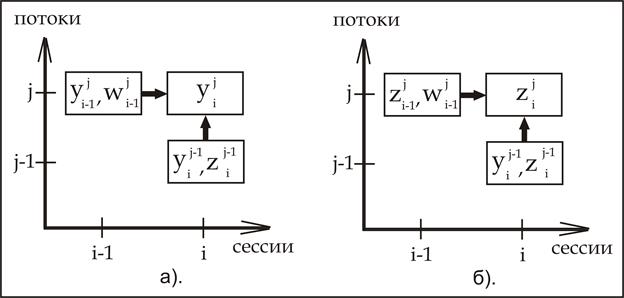
Рис. 1. Расчётные схемы для вычисления и .
а) зависимость от значений функций 
предыдущих сессий и потоков;
б) зависимость от значений функций предыдущих сессий и потоков.
Будем предполагать, что студенты за весь срок обучения проходят девять промежуточных этапов учета знаний. Изменения, которые происходят за это время в группе 
-го потока претендентов на поступление в аспирантуру, представлены на рисунке 2.
Рис. 2. Динамика потоков, влияющих на группу претендентов при поступлении в аспирантуру для -го потока студентов.
Предполагается, что известна статистическая информация в разрезе девяти сессий по 
потокам: 
, 
.
Коэффициенты 
, первого уравнения системы (5) находятся как решение системы линейных алгебраических уравнений следующего вида:
, , (6)
где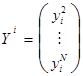 
, 
, 
.
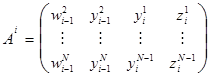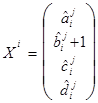Коэффициенты 
, второго уравнения системы (5) находятся как решение системы линейных алгебраических уравнений следующего вида:
, , (7)
где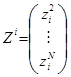 
, 
, 
.
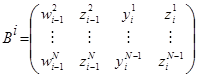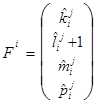Найденные параметры из систем линейных алгебраических уравнений (6) и (7) подставляются в итерационную систему (5). Для 
-го потока итерационная система (5) примет вид:
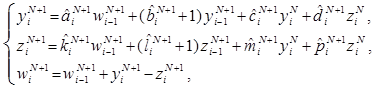
При условии, что 
известны, итерационная система (8) позволяет прогнозировать динамику численности претендентов на поступление в аспирантуру на основе статистических данных за несколько лет, предшествующих прогнозируемому отрезку времени.
Рецензенты:
Малыханов Юрий Борисович, доктор физико-математических наук, профессор, профессор кафедры физики и методики обучения физике физико-математического факультета ФГБОУ ВПО «Мордовский государственный педагогический институт имени М.Е. Евсевьева», г. Саранск.
Вельмисов Петр Александрович, доктор физико-математических наук, профессор, заведующий кафедрой «Высшая математика» Ульяновского государственного технического университета, г. Ульяновск.