Современные изменения, происходящие в обществе, существенным образом повлияли на роль и приоритеты общего образования. Целесообразность подготовки выпускника общеобразовательной школы к инновационным преобразованиям общества стало жизненно необходимым условием его самоопределения и самореализации. В качестве одного из механизмов создания указанных условий, по нашему мнению, следует рассматривать приобретение опыта к анализу и исследованию ситуаций, с которыми выпускнику приходится сталкиваться после окончания школы при выборе своего профессионального пути.
Неслучайно в Федеральном стандарте среднего (полного) общего образования индивидуальная проектно-исследовательская деятельность учащихся рассматривается в качестве класса универсальных учебных действий, которые представлены в качестве конечных результатов образования [8].
Поставленная задача является в настоящее время одним из приоритетных направлений содержания общего образования, которое должно прослеживаться на всех школьных предметах, в том числе и на математике.
Процесс обучения математике в 10–11 классах позволяет на его основе развивать индивидуальную проектно-исследовательскую деятельность учащихся. Это связано с тем, что, во-первых, курс математики 10–11 классов является завершающим, систематизирующим и обобщающим разделом школьной математики.
Во-вторых, содержательный компонент математики 10–11 классов раскрывает основные идеи и пути дальнейшего развития математического знания, использование которого позволяет усвоить фундаментальные основы построения математического анализа, установить связи с предметами естественнонаучного цикла.
В-третьих, в процессе обучения математике в 10–11 классах учащиеся овладевают математическим инструментарием – математическими моделями. Их применение позволяет показать учащимся универсальность математического аппарата как средства описания различных явлений и процессов. Организация математической деятельности предполагает мысленное экспериментирование с тем или иным материалом с целью прослеживания его взаимосвязи.
Как видим, резерв содержательного и процессуального компонентов процесса обучения математике в 10–11 классах обладает большим потенциалом для развития индивидуальной проектно-исследовательской деятельности учащихся.
Под индивидуальной проектно-исследовательской деятельностью в исследовании понимается процесс достижения цели, который выстраивается по индивидуальной образовательной траектории на основе самостоятельного поиска теоретических знаний, предвидения и прогнозирования способов и процессов деятельности, и завершается реальным практическим или теоретическим результатом.
Создание индивидуальной образовательной траектории предполагает выявление этапов индивидуальной проектно-исследовательской деятельности. Основываясь на результатах работы Н. В. Матяш [4], в исследовании были выделены этапы индивидуальной проектно-исследовательской деятельности:
- ситуационно-исследовательский этап, целью которого является появление интереса у обучающихся на основе действия учебно-познавательных мотивов, осознание проблемы и формулирование цели деятельности, её планирование, поиск и отбор информации по теме, выбор средств и инструментария;
- инструментально-операциональный этап, целью которого является обработка и осмысление информации обучающимся, самоконтроль деятельности, установление соответствия её поставленной цели, выполнение соответствующих технологических операций, предусмотренных разработанным планом, оформление результата;
- рефлексивно-оценочный этап, его цель – формулировка выводов по соответствию результатов деятельности с заданной целью, проверка рациональности выполненных действий, поиск альтернативных путей решения и обозначение дальнейших перспектив развития проблемы, представление результата своей деятельности в виде сообщения, презентации, публикации и др.
Этапы индивидуальной проектно-исследовательской деятельности тесно связаны с этапами процесса обучения математике, на каждом из которых используются задачи-ситуации.
Под задачей-ситуацией понимается данная в определенных условиях и обстоятельствах цель деятельности, которая достигается определенной последовательностью действий, соответствующих сложившейся ситуации. Последовательность действий предполагает: осознание ситуации, построение модели, её теоретическое обоснование и практическое применение. В соответствии с этапами развития индивидуальной проектно-исследовательской деятельности выделены виды задач-ситуаций: на прогнозирование, на планирование, на создание проекта.
Различные математические ситуации, возникающие в процессе решения задач-ситуаций, разрешимы с использованием эксперимента. Гибкость и вариативность решения математической ситуации, установление причинно-следственных, внутрипредметных и межпредметных связей в процессе проведения эксперимента также подтверждает целесообразность его использования при осуществлении проектно-исследовательской деятельности в процессе обучения математике в 10–11 классах.
Определяя роль и место эксперимента в процессе обучения физике, Т. Н. Шамало подчеркивает его полифукциональность. При этом автор обращает внимание, что роль эксперимента заключается не только в создания понятийного аппарата определённой предметной области, но и в развитии мышления в целом [9, с.69].
По мнению В. И. Загвязинского, эксперимент – самый точный метод изучения явлений, фиксирования фактов, слежения за изменением и развитием объекта исследования [2].
В. В. Давыдов в своих работах употребляет понятие «мыслительный эксперимент», который, по мнению автора, нацеливает учащихся на получение знаний как результата преобразования заданного материала, позволяющего вскрыть в нём существенные отношения и проследить происхождение внешних проявлений изучаемого материала [1].
В широком смысле эксперимент представляет собой целенаправленное и жестко контролируемое действие исследователя на объект для изучения его различных сторон, связей и отношений. По мнению Л. А. Михайлова [5], С. Х. Карпенкова [3], В. В. Налимова [7] и др., в любом эксперименте можно выделить следующие этапы:
- подготовительный этап ориентирован на теоретическое обоснование эксперимента, формулировку гипотезы, его планирование, создание модели, выбор условий и средств исследования;
- этап сбора экспериментальных данных направлен на работу с моделью, выполнение соответствующих технологических операций, многократную повторность измерений и строгий учёт факторов, влияющих на исследуемый объект;
- этап обработки результатов содержит анализ и интерпретацию результатов эксперимента, сопоставление их с гипотезой, установление причинно-следственных связей между заданными условиями и характеристиками исследуемого объекта.
На всех этапах эксперимента важна мыслительная деятельность экспериментатора, включающая отделение фактов, непосредственно влияющих на объект исследования, искусственное выделение некоторых его свойств, признаков или отношений, которые и являются предметом изучения, что способствует глубокому пониманию сути явлений и процессов.
На основе проведённого в исследовании контент-анализа видно, что этапы индивидуальной проектно-исследовательской деятельности и этапы эксперимента находятся в тесной связи, повторяют друг друга или являются взаимозаменяемыми (рис.1).
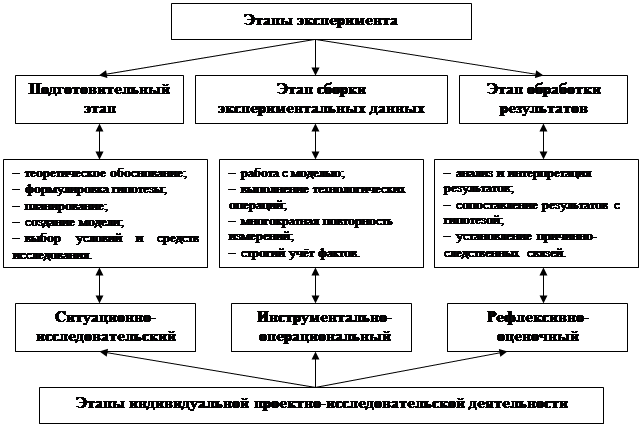
Рис. 1. Сопоставление этапов индивидуальной проектно-исследовательской деятельности с этапами эксперимента
Приведём пример задачи-ситуации на прогнозирование, направленной на развитие индивидуальной проектно-исследовательской деятельности, для решения которой необходимо использование эксперимента. Тема: «Общие методы решения уравнений» [6].
Цель: сформировать представление учащихся об общих идеях и методах решения уравнений.
1. Прочитайте теоретический материал об общих методах решения уравнений и выделите особенности каждого из них (подчеркните их в тексте):
Метод замены уравнения ![]() уравнением
уравнением ![]()
Такой метод решения уравнений применяется:
- при решении показательных уравнений, когда переходим от уравнения ![]() к уравнению
к уравнению ![]() ;
;
- при решении логарифмических уравнений, когда переходим от уравнения ![]() к уравнению
к уравнению ![]() ;
;
- при решении иррациональных уравнений, когда переходим от уравнения ![]() к уравнению
к уравнению ![]() .
.
Этот метод можно применять только в том случае, когда функция ![]() монотонна, т.е. принимает каждое своё значение по одному разу. Если
монотонна, т.е. принимает каждое своё значение по одному разу. Если ![]() – не монотонная функция, то указанный метод применять нельзя, так как возможна потеря корней.
– не монотонная функция, то указанный метод применять нельзя, так как возможна потеря корней.
Метод разложения на множители
Уравнение ![]() можно заменить совокупностью уравнений
можно заменить совокупностью уравнений 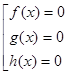 . Решив уравнения этой совокупности, нужно взять те их корни, которые принадлежат области определения исходного уравнения, а остальные отбросить как посторонние.
. Решив уравнения этой совокупности, нужно взять те их корни, которые принадлежат области определения исходного уравнения, а остальные отбросить как посторонние.
Метод введения новой переменной
Если уравнение ![]() удалось преобразовать к виду
удалось преобразовать к виду ![]() , то нужно ввести новую переменную
, то нужно ввести новую переменную ![]() и решать уравнение
и решать уравнение ![]() , а затем решить совокупность уравнений:
, а затем решить совокупность уравнений: 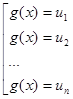 , где
, где ![]() – корни уравнения
– корни уравнения ![]() .
.
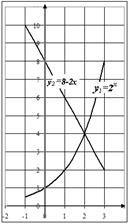
Функционально-графический метод
Идея этого метода решения уравнения ![]() заключается в следующем, нужно построить графики функций
заключается в следующем, нужно построить графики функций ![]() и
и ![]() , а затее найти точки их пересечения. Корнями уравнения служат абсциссы этих точек.
, а затее найти точки их пересечения. Корнями уравнения служат абсциссы этих точек.
2. Установите соответствие между решёнными уравнениями и методом их решения (рис. 2):
|
Ответ:
|
|
Метод замены уравнения |
|
Пример 2:
Заменим
Ответ: |
|
Метод разложения на множители |
|
Пример 3:
Ответ: |
|
Функционально-графический метод |
|
Пример 4:
Ответ: |
|
Метод введения новой переменной |
Рис. 2. Соответствие между уравнениями и методом их решения
3. Решите уравнения и разбейте предложенные уравнения на группы по методам решения (табл. 1).
Таблица 1
Примеры уравнений по методам решения
|
Методы решения уравнений |
Метод замены уравнения |
Метод введения новой переменной |
Метод разложения на множители |
Функционально-графический метод |
|
Группы уравнений |
|
|
|
|
![]() ;
; ![]() ;
; ![]() , ;
, ; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
Использование задач-ситуаций, для решения которых необходимо применять эксперимент, выступает механизмом развития индивидуальной проектно-исследовательской деятельности обучающихся в учебном процессе по математике в 10–11 классах.
Рецензенты:
Мерлина Н. И., доктор педагогических наук, кандидат физико-математических наук, профессор, профессор кафедры прикладной математики Чувашского государственного университета им. И. Н. Ульянова, г. Чебоксары.
Уткина Т. И., доктор педагогических наук, профессор, заведующий кафедрой алгебры, геометрии, теории и методики обучения математике Орского гуманитарно-технологического института ГБОУ ВПО «Оренбургский государственный университет», г. Орск.




 Пример 1:
Пример 1:
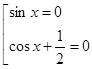 ,
, 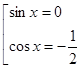 ,
, 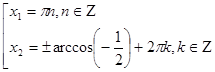 ,
, 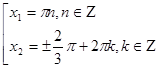 .
.