Введение
При разложении ТБО и ПО на полигонах образуется биогаз – газовая смесь углеводородов, углекислого газа, сероводорода, ксилола, аммиака и др. Некоторые его компоненты токсичны и взрывопожароопасны. Экологическая опасность рассеивания биогаза вызвана загрязнением прилегающей к полигону территории. Известные методики расчёта поля концентраций примеси, как ОНД-86, нормальное (Гауссово) распределение являются в большей части аппроксимациями и не рассматривают детально процессы, происходящие при обтекании потоком препятствий, коими являются здания, сооружения и сами полигоны, которые имеют внушительные размеры и способны существенно влиять на конвективные и турбулентные процессы переноса примеси.
Цель статьи – численное моделирование рассеивания биогаза с полигонов ТБО и ПО с помощью решения уравнений диффузии и Навье-Стокса. Полученные результаты можно использовать:
- для оценки загрязнённости атмосферного воздуха в зоне влияния полигонов ТБО и ПО;
- при выборе места расположения будущих полигонов ТБО и ПО;
- при обосновании размеров санитарно-защитных зон полигонов ТБО и ПО;
- при рекультивации и оценке эффективности мер по снижению загрязнения атмосферного воздуха биогазом (утилизация биогаза, выбор оптимального расположения и характеристик газодренажных скважин и т.д.).
Для моделирования рассеивания биогаза предложено численное решение дифференциального уравнения конвективно-диффузионного переноса примеси в атмосферном воздухе, которое имеет вид:
![]() (1)
(1)
где u, v, w – компоненты скоростей ветра вдоль осей х, у, z соответственно; kx, ky, kz – коэффициенты турбулентности вдоль осей х, у, z соответственно; ![]() – функция эмиссии примесей. Для упрощения расчётов в дальнейшем в уравнении (1) принято
– функция эмиссии примесей. Для упрощения расчётов в дальнейшем в уравнении (1) принято ![]() , а учёт эмиссии биогаза производится с помощью граничных условий – концентрации на поверхности полигона [4].
, а учёт эмиссии биогаза производится с помощью граничных условий – концентрации на поверхности полигона [4].
Коэффициенты турбулентности целесообразно определять с помощью модели Дж. Смагоринского, учитывающей появление дополнительной турбулентности, вызванной завихрённостью, с помощью уравнений [3]:
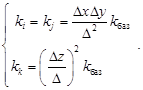 (2)
(2)
где ![]() – масштаб для мелких вихрей определяется шириной трёхмерной ячейки, kбаз – базовый коэффициент турбулентности, определяющийся как:
– масштаб для мелких вихрей определяется шириной трёхмерной ячейки, kбаз – базовый коэффициент турбулентности, определяющийся как:
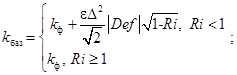 (3)
(3)
где kф – фоновый коэффициент турбулентности, kф = 1-15 м2/с; ε = 0,1-0,4; Def (x; y; z; t) – функция диссипации или деформации, определяемая как
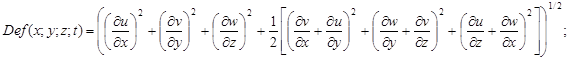 (4)
(4)
Ri – локальное число Ричардсона, определяющееся с помощью уравнения:
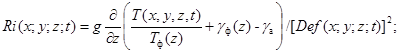 (5)
(5)
где T – температура; γф(z) – градиент фоновой температуры, γа – адиабатический градиент температуры.
Тепловизионная съёмка различных полигонов ТБО и ПО, проводившаяся нами в работе [5], показала, что выброс биогаза на полигоне можно считать «холодным», т.е.:
Тбиогаза ≈ Тф.; (6)
где Тбиогаза и Тф – температуры выбрасываемого биогаза и фоновая.
При моделировании рассеивания выбросов от низких источников наибольший интерес представляет нижняя граница приземного слоя атмосферы, к которой относят нижние 50-100 м. В ней вертикальные потоки тепла и импульса остаются постоянными по высоте и проявляется устойчивое состояние атмосферы. Учитывая небольшую вертикальную протяжённость этого слоя, можно принять условие равновесной (безразличной) стратификации, когда вертикальный поток тепла равен нулю, а изменение температуры происходит по адиабатическому закону [1]. При этом вертикальный градиент температуры равен адиабатическому ga = 0,01ºC/м.
При безразличной стратификации атмосферы для «холодных» выбросов ![]() система (3) примет более простой вид:
система (3) примет более простой вид:
![]() (7)
(7)
Шероховатая, химически активная поверхность способна к частичному удерживанию биогаза на поверхности с дальнейшим поглощением. При аэробных процессах в составе биогаза преобладает углекислый газ, поглощаемый при фотосинтезе. Остальные его компоненты отравляют почву и растения. Диффузию газа на границе «воздух-почва» можно выразить уравнением:
![]() (8)
(8)
где β – константа взаимодействия (для гладкой, химически инертной поверхности β ≈ 0).
В начальный момент времени (без учёта фона) значения концентрации примесей биогаза равны нулю. На бесконечно большом расстоянии от полигона значения концентраций примесей также равны нулю. Это можно выразить в виде условий:
![]() (9)
(9)
Для решения задачи турбулентного движения газа используется прямое моделирование «DNS», основанное на решении нестационарных уравнений Навье-Стокса (для несжимаемой среды):
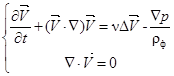 ; (10)
; (10)
где ν – кинематическая вязкость, p – давление, ![]() – вектор скорости.
– вектор скорости.
Для набегающего потока (входящего в расчётную область) давление p принимается равным атмосферному, v = w = 0, профиль скоростей ветра при нейтральной стратификации атмосферы описывается уравнением Кармана [3]:
![]() . (11)
. (11)
где u* – динамическая скорость, м/с; z0 – параметр шероховатости поверхности; ϛ – коэффициент Кармана ϛ = 0,4; Hср – средняя высота ветровых преград (застройки, лесополосы); C – коэффициент сопротивления. Значения z0 и C для некоторых поверхностей приведены в табл. 1.
Табл. 1. Значения коэффициентов z0 и С для некоторых типов поверхностей [3]
|
Тип поверхности |
z0, см |
С×103 |
|
Песок |
0,01-0,1 |
1,2-1,9 |
|
Степь |
1-4 |
3,4-5,2 |
|
Высокая трава |
4-10 |
5,2-7,6 |
|
Пригородная застройка |
20-40 |
10,5-15,4 |
|
Центры городов |
200-300 |
61,8-110,4 |
Профиль скоростей ветра удобно также задавать уравнением, использующимся при моделировании в аэродинамических трубах [3]:
![]() ; (12)
; (12)
где z0 – заданная высота (например, высота флюгера); u0 – скорость ветра на заданной высоте z0; B – коэффициент аппроксимации, B = 1/7.
Для решения задач, связанных с переносом турбулентным потоком скалярных субстанций, при решении дифференциальных уравнений используют схему расщепления по физическим процессам. Согласно принципам расщепления конечно-разностное интегрирование уравнений гидродинамики и конвективно-диффузного переноса скалярной субстанции на каждом шаге по времени Dt осуществляется в два этапа. На первом этапе рассчитываются гидродинамические параметры. На втором этапе на основе рассчитанных гидродинамических полей решаются уравнения диффузии.
В качестве примера приведено моделирование рассеивания метана (основного компонента биогаза) на полигоне «Центральный» Волгоградской области в 2007 г. Моделирование производилось в программной среде Mat lab/Femlab. Набивающий поток принят по логарифмической зависимости, значения kф = 4 м2/с; ε = 0,2. На рис. 1 изображены поля скоростей ветра и концентраций метана.
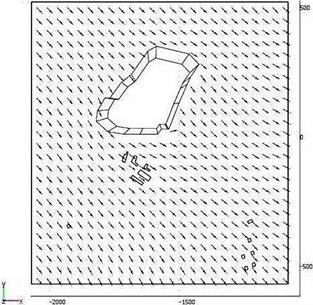
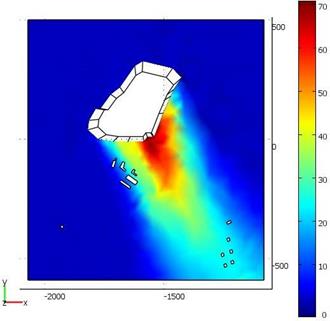
Рис. 1. Поле скоростей ветра при обтекании полигона (слева) и поле концентраций метана в зоне влияния свалки «Центральный» (справа)
Табл. 2. Сравнение значений концентраций метана в зоне влияния полигона ТБО «Центральный» в 2007 г., полученных различными способами
|
Контрольная точка |
Значения концентраций метана, доля ОБУВ |
||
|
экспериментальное |
расчётное по ОНД-86 [5] |
расчётное с помощью предложенной модели |
|
|
Санитарно-защитная зона, 10 м от полигона |
72±14,4 |
5,5 |
67,2 |
|
Санитарно-защитная зона, 50 м до полигона |
21,2±4,2 |
17,5 |
23,1 |
|
Центр пос. Овражный |
22,5±4,5 |
23,5 |
24,0 |
В заключение отметим, что моделирование на основе решений уравнений Навье-Стокса и диффузии даёт результат значительно лучше, чем методика ОНД-86. Результаты расчёта по предложенной модели близки к опытным данным. Моделирование выбросов биогаза на стадии эксплуатации, рекультивации полигонов можно рассматривать как один из аспектов информационного моделирования, направленного на обеспечение экологической безопасности при обращении с ТБО и ПО.
Рецензенты:
Дацюк Тамара Александровна, доктор технических наук, профессор, декан факультета инженерной экологии и городского хозяйства, заведующий кафедрой общей и строительной физики, ФГБОУВПО «СПБГАСУ», г. Санкт-Петербург.
Ивочкина Нина Михайловна, доктор физико-математических наук, профессор, профессор кафедры математики. ФГБОУВПО «СПбГАСУ», г. Санкт-Петербург.



