Введение
Доля измерений линейных размеров и перемещений во многих областях техники составляет до 95 % всех контролируемых параметров [6]. Результаты измерений широко используются при физическом и технологическом моделировании пространственно сложных объектов, а также при мониторинге силовых энергоустановок в процессе эксплуатации для обеспечения безопасной и бесперебойной работы. Совершенствование методов высокоточной бесконтактной диагностики геометрических параметров труднодоступных объектов является актуальной научной и технической проблемой.
Во многих отраслях промышленности и энергетики необходимо обеспечивать динамический мониторинг критических геометрических параметров движущихся объектов в течение жизненного цикла машин и механизмов. Своевременное обнаружение критического режима работы может снизить негативные последствия поломки сложного механизма и существенно сократить издержки восстановительного ремонта устройства. В частности, диагностика динамической формы вращающихся объектов крайне актуальна для энергетической отрасли, а именно для мониторинга геометрии формы ротора энергоагрегатов тепло- и гидроэлектростанций. Наиболее перспективно использовать бесконтактные методы диагностики, поскольку силовые установки электростанций представляют собой закрытое сложное устройство, прошедшее большое количество технологических испытаний, и внесение изменений в его конструкцию может быть недопустимо.
Цель исследований
Цель работы заключается в создании метода лазерной диагностики динамической формы вращающихся объектов, применимого для решения актуальной задачи диагностики динамической формы ротора энергоагрегата электростанции.
Методы исследований
Для бесконтактной диагностики динамической формы вращающихся объектов известны решения на основе использования малогабаритных емкостных датчиков [5]. Однако эти датчики необходимо устанавливать в непосредственной близости к поверхности измеряемого объекта, и, в случае аварийного режима работы, датчики с высокой вероятностью будут повреждены и выйдут из строя. Эксплуатация таких измерителей возможна в довольно узком диапазоне температуры и влажности окружающей среды, так как точность работы емкостных измерителей значительно зависит от постоянства содержания паров воды в воздухе.
Известно оптоэлектронное устройство для бесконтактного измерения динамической формы вращающегося объекта [3], использующее оптопары на основе инфракрасных излучателей и приемников, позиционированных на заданном расстоянии от поверхности полюсов ротора. Недостатками системы являются требование к размещению непосредственно датчиков в воздушном зазоре действующей электрической машины, а также сложность и неоднозначность калибровки датчиков после их установки в зазор.
Известны лазерные устройства для измерения расстояний до объектов и скорости их движения на основе FMCW-лидаров, использующие метод линейной модуляции частоты излучения лазера. Преимущество измерительных устройств на основе линейной модуляции частоты излучения лазера заключается в возможности быстрых и точных дистанционных измерений через узкий протяженный канал и использовании одного объектива для излучения лазерного луча и приема отраженного света, не требующих изменения конструкции измеряемых машин [4].
Предлагаемый метод динамического мониторинга геометрии вращающегося объекта основан на линейной модуляции частоты излучения одномодового полупроводникового лазера, обработке оптоэлектронного сигнала и фазовом усреднении полученной информации с ее необходимой статистической обработкой. Частота лазерного излучения модулируется по треугольному закону. Для управления частотой лазера изменяется ток его накачки. Температура полупроводникового кристалла лазера изменяется при изменении тока накачки, что вызывает изменение показателя преломления материала. Произведение показателя преломления материала лазера и физической длины лазерного резонатора равно оптической длине пути резонатора Ld (так называемой эффективной длине резонатора) и зависит от величины тока накачки лазерного диода. Частота модуляции тока накачки лазера определяет быстродействие цикла измерения расстояния, частота которого может принимать значения от 0,1 до 10 кГц.
Для измерения геометрии вращающегося объекта лазер закрепляют неподвижно, излучение направляют к поверхности вращающегося объекта по нормали. Отраженное излучение от поверхности вращающегося объекта собирается и фокусируется коллиматорной линзой и возвращается в резонатор лазера. В резонаторе лазерного диода происходит смещение излученного и принятого лазерного излучения. Частота отраженного света равна:
![]() , (1)
, (1)
где dt – время хождения луча до поверхности ротора и обратно:
![]() , (2)
, (2)
здесь L – расстояние до поверхности, с – скорость света. Поскольку частота излучения лазера меняется по линейному закону, то в результате интерференции в резонаторе лазера отраженного света со светом с текущей рабочей частотой лазера возникает дополнительная частота биения, фиксируемая встроенным фотодиодом. Дополнительная частота биений пропорциональна расстоянию до поверхности вращающегося объекта:
![]() , (3)
, (3)
где ![]() – частота биений,
– частота биений, ![]() – период модуляции,
– период модуляции, ![]() -амплитуда частотной модуляции лазера (рис.1).
-амплитуда частотной модуляции лазера (рис.1).
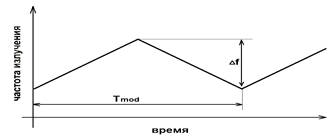
Рисунок 1. Принцип частотной модуляции лазера
В случае движения поверхности объекта в направлении излучения лазера частота биения будет смещена на величину доплеровского сдвига частоты:
![]() . (4)
. (4)
Этот доплеровский сдвиг на восходящем и нисходящем фронте модуляции частоты лазера будет иметь одинаковую величину, но различный знак. Для компенсации доплеровского сдвига необходимо вычислять частоту биений как полусумму частоты биений на восходящем фронте модуляции (F1) и на нисходящем фронте (F2):
![]() , (5)
, (5)
откуда
![]() . (6)
. (6)
Так как мы проводим измерения вращающегося объекта, то для уменьшения погрешности измерения необходимо фазовое усреднение данных по нескольким периодам вращения. Для реализации фазового осреднения можно использовать сигнал с отметчика, представляющего собой оптический модуль, генерирующий синхросигнал, привязанный к начальной фазе вращения измеряемого объекта.
Простейший алгоритм вычисления периода отметчика – определение времени между двумя срабатываниями сигнала отметчика. Данный метод, однако, подвержен влиянию дребезга, может использоваться только для прямоугольного сигнала отметчика и имеет точность, равную дискрету времени.
Для непрямоугольного периодического сигнала можно реализовать алгоритм определения периода методом вычисления спектра сигнала и определения главной частоты. Данный подход требует большой вычислительной сложности (O(N*log(N))) и плохо подходит для обработки сигналов с длительным периодом.
Для решения данной проблемы предложен метод вычисления периода как максимума автокорреляционной функции сигнала отметчика. Сложность метода соизмерима с преобразованием Фурье (O(N*log(N))). Для снижения сложности алгоритма исходные данные дополнительно прореживаются. Получив автокорреляционную функцию прореженного сигнала, определяем время второго максимума, которое соответствует периоду сигнала синхронизации.
Для субдискретной точности используется следующий метод определения пика автокорреляционной функции. В непосредственной близости от пика проводят прямую y = const (рисунок 2). Автокорреляционную функцию аппроксимируют как кусочно-линейную и аналитически находят точные координаты пересечения прямой y = Const с отрезками автокорреляционной функции. Координату середины отрезка, соединяющего точки пересечения, считают координатой максимума автокорреляционной функции.
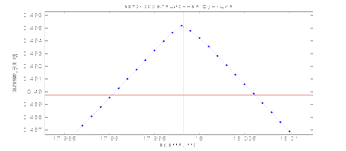
Рисунок 2. Метод определения середины пика с субдискретной точностью. Пик автокорреляционной функции
Экспериментально установлено, что при прореживании данных в соотношении 1:100 погрешность определения периода вращения методом вычисления середины пика автокорреляционной функции с субдискретной точностью составляет менее 1 мкс. Таким образом, показано, что предложенный метод определения середины пика автокорреляционной функции позволяет сократить сложность алгоритма вычисления периода оборота измеряемого объекта примерно в 100 раз.
Фазовое усреднение производится с привязкой к начальной фазе вращения объекта, восстанавливаемой при анализе периодически воспроизводящихся на каждом обороте получаемых данных о расстоянии. В результате выполнения операций усреднения и дискриминации выбросов получается сглаженная "развертка" графика расстояния от измерительного датчика до поверхности объекта в зависимости от угла поворота объекта [2].
Практическая реализация
Предложенный метод лазерной диагностики динамической формы вращающихся объектов реализован в составе лазерной системы для динамического мониторинга геометрии нагруженного ротора генератора гидроэлектростанции [1]. Лазерная система опробована на действующем гидрогенераторе ГЭС. Впервые получены результаты измерений геометрии ротора действующего нагруженного гидрогенератора № 4 Саяно-Шушенской ГЭС (тип СВФ/1285-42V4, 640 МВт). Получен фазово-осредненный профиль поверхности ротора в реальном времени. Усреднение проводилось по 10 периодам вращения ротора.
При измерении производилось усреднение по точкам одного полюса. Для этого на каждом полюсе фазово-осредненной диаграммы выделялись отсчеты, заведомо принадлежащие поверхности полюса, а не его краям или подполюсу. Оказалось, что для наилучшего результата достаточно брать для усреднения 6 отсчетов на каждом полюсе. Такие отсчеты были автоматически отобраны и усреднены.
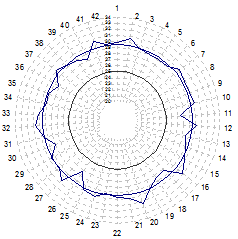
Рисунок. 3. Результаты измерений геометрии ротора гидрогенератора
Результаты измерений представлены на рисунке 3. Погрешность измерений методом на основе лазерной технологии даже в опытном исполнении не превышала 1 %. Испытания показали, что система вписывается в существующую технологическую цепочку ОАО «Саяно-Шушенская ГЭС имени П. С. Непорожнего» и не нарушает работу существующего оборудования.
Выводы
Предложен метод лазерной диагностики динамической формы вращающихся объектов. Метод основан на линейной модуляции частоты излучения лазера и фазовом накоплении статистических данных. Предложен метод субдискретного определения пика автокорреляционной функции, позволяющий сократить вычислительные ресурсы вычислительной машины, обрабатывающей сигнал измерительной системы в 100 раз. Предложенные методы позволили проводить измерения геометрии быстро движущейся поверхности измеряемого объекта через узкий протяженный канал в реальном времени. Предложенный метод реализован в составе лазерной системы для динамического мониторинга геометрии нагруженного ротора генератора гидроэлектростанции. Методы в составе лазерной системы опробованы на действующем сверхмощном нагруженном гидрогенераторе ГЭС. Получены результаты измерений геометрии ротора действующего гидрогенератора с погрешностью менее 1 %. Показана работоспособность предложенных методов в реальных производственных условиях.
Работа выполнена при частичной поддержке Министерства образования и науки РФ в рамках реализации ФЦП «Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007–2013 годы» (ГК № 11.519.11.6022) и при частичной поддержке Совета по грантам Президента Российской Федерации для поддержки молодых российских ученых и ведущих научных школ (ГК № МК-2762.2013.8).
Рецензенты:
Бердников Владимир Степанович, д-р физ.-мат. наук, профессор, зав. лабораторией, Институт теплофизики им. С. С. Кутателадзе СО РАН, г. Новосибирск.
Лежнин Сергей Иванович, д-р физ.-мат. наук, профессор, г.н.с., Институт теплофизики им. С. С. Кутателадзе СО РАН, г. Новосибирск.



