Для расчета движения частиц в закрученном потоке обычно используются упрощенные модели, в которых учитываются только наиболее значимые силы [1; 4]. В вертикальном восходящем или нисходящем закрученном потоке без учета влияния турбулентных пульсаций газа такими силами являются сила тяжести, сила Кориолиса и центробежная сила. Система уравнений движения частицы может быть записана в виде [1; 4; 5]:
, (1)
, (2)
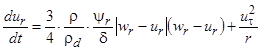, (3)
где uz, ut и ur - осевая, окружная (тангенциальная) и радиальная составляющие скорости частицы, м/с; wz, wt и wr - осевая, окружная (тангенциальная) и радиальная составляющие скорости газа, м/с; d - диаметр частиц, м; rd и r - плотности материала частиц и газа, кг/м3; g - ускорение свободного падения (знак «+» относится к нисходящему потоку, «-» к восходящему), м/с2; r - радиус-вектор (расстояние от оси канала), м; yz, yt и yr - коэффициенты сопротивления в осевом, окружном (тангенциальном) и радиальном направлениях.
Для расчета траекторий движения частицы в закрученном потоке необходимо задать законы изменения осевой, окружной и радиальной составляющих скорости потока по длине и радиусу канала. Для приближенного расчета используются эмпирические зависимости и упрощенные формы полей скоростей [4]. Обычно считается, что осевая составляющая скорости газа одинакова по сечению канала, радиальная равна нулю, тангенциальная подчиняется закону вращения твердого тела в приосевой зоне и потенциальному закону - в периферийной [5]. Затухание закрутки, влияние турбулентных пульсаций газа и вторичный унос частиц с поверхности канала при оценочных расчетах, как правило, не учитывается.
При постоянной осевой составляющей скорости потока и стоксовском режиме обтекания скорость относительного движения wz-uz принимает постоянное максимальное предельное значение gt, при этом для восходящего потока uz = wz - gt, для нисходящего - uz = wz+gt [4]. Для высокодисперсных частиц скоростью седиментации можно пренебречь и считать, что осевая скорость частиц в закрученном потоке в цилиндрическом канале равна осевой скорости газа [4].
При Red < 1 уравнение движения частицы в тангенциальном направлении (2) принимает вид
(4)
или
, (5)
где j - угол поворота частицы при вращении вокруг оси канала, рад, t = d2rd/(18m) - время релаксации, с.
Для высокодисперсных частиц первое слагаемое в скобках в уравнении (5) гораздо меньше второго и им можно пренебречь (это равносильно допущению о малости силы Кориолиса). Тогда уравнение (5) примет вид
. (6)
Решение уравнения (6) имеет вид
, (7)
т.е. угловая скорость вращения частицы вокруг оси канала и окружная (тангенциальная) составляющая скорости частицы
, 
. (8)
При t >> t с высокой степенью точности j » j0+wt, dj/dt » w и ut » wt. Поэтому в большинстве практически значимых случаев можно принять, что в тангенциальном направлении скорость частицы равна скорости газа.
В радиальном направлении на частицу, кроме сил аэродинамического сопротивления, действует только центробежная сила. Для высокодисперсных частиц при Red < 1, ut = wt и wr = 0 уравнение движения (3) может быть записано в виде:
. (9)
Если в уравнениях (3) и (9) пренебречь силой инерции (для высокодисперсных частиц при сравнительно небольших угловых скоростях), что равносильно пренебрежению разгонным участком, то расчет движения частиц можно производить, приравняв силы аэродинамического сопротивления и центробежную силу [3]. Тогда уравнение (9) можно записать в виде
. (10)
Решением уравнения (10) является выражение [2]
r = r0exp(tw02t). (11)
Для расчета равновесных траекторий движения частиц в закрученном потоке газа и оценки адекватности предложенных упрощенных решений можно использовать выражение для тангенциальной скорости газа, учитывающее затухание крутки потока [6]:
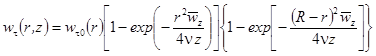. (12)
где wt0(r) - функция распределения окружной (тангенциальной) скорости во входном сечении канала, м/с, R - радиус канала, м; n - кинематическая вязкость газа, м2/c.
Рассмотренные модели движения частиц в закрученном потоке газа дают лишь общее представление о поведении частиц, хотя и определяют основные тенденции развития гидродинамических процессов и влияние основных параметров [4]. Основными недостатками таких моделей является отсутствие учета турбулентных пульсаций газа и связанных с ними отклонений траекторий частиц от равновесных. Так как эти отклонения носят стохастический характер, то и анализ поведения частиц должен включать использование как детерминированных, так и вероятностных методов, в частности – с использованием вероятностно-статистического подхода к моделированию двухфазных потоков [7]. При этом, как и для незакрученных потоков, от расчета траекторий частиц и определения положения частиц в каждый момент времени необходимо перейти к определению вероятности нахождения частицы в каждой точке канала, а для совокупности большого числа частиц – к распределению частиц по длине и сечению канала, т.е. расчету поля их концентраций и его изменения во времени или по длине канала [7].
В турбулентном потоке аэрозольные частицы могут перемещаться как вместе с газом или под воздействием внешних сил (детерминированное движение), так и посредством диффузии (молекулярной или турбулентной). В соответствии с этим для описания поведения частиц используются диффузионная модель, учитывающая как детерминированную, так и диффузионную составляющие движения [8; 9]:
, (13)
где n - концентрация частиц, м-3; Dd - коэффициент диффузии, м2/с.
Если рассматривать движение частицы как последовательность скачкообразных перемещений длиной l через малые промежутки времени Dt в одном из шести возможных направлений в цилиндрической системе координат z-t-r, то траектория ее движения будет представлять собой трехмерную ломаную из отрезков длиной l и скорость перемещения в каждом из направлений будет определяться соответствующими вероятностями pi: p+z, p-z, p+t, p-t, p+r и p-r (при этом p+z(t) + p-z(t) + p+t(t) + p-t(t) + p+r(t) + p-r(t) = 1). Для осесимметричного закрученного потока можно перейти к вращающейся системе координат и рассматривать двухмерную задачу и движение частиц в одном из четырех возможных направлений с вероятностями p+z, p-z, p+r и p-r (при этом p+z(t) + p-z(t) + p+r(t) + p-r(t) = 1).
В системе координат, перемещающейся вместе с газом с постоянной осевой скоростью, перемещения частицы в трех направлениях из четырех обусловлены только случайными воздействиями турбулентных пульсаций газа (два направления вдоль осевой координаты и в направлении от поверхности канала), а в одном направлении (к поверхности канала) - совместным действием центробежной силы и турбулентной диффузии. Значения вероятностей перемещения частицы в каждом из направлений можно выразить с помощью параметра перехода k, который может принимать значения от 0 до 1: значение k = 1 соответствует предельному случаю чистой турбулентной диффузии, а k = 0 - предельному случаю строго детерминированного движения [10]. Вероятность диффузии в любом направлении одинакова, и поэтому p+z = p-z = p-r = k/(2s) = k/4, вероятность движения частицы к поверхности канала в результате совместного действия детерминированного и стохастического механизмов p+r = (1-k)+k/(2s) = 1-3k/4 (легко убедиться, что при любом значении k сумма вероятностей равна единице).
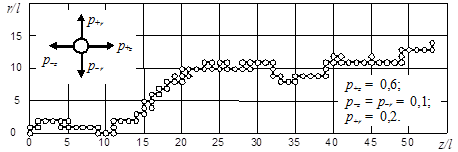
Рис. 1. Схема и пример дискретного вероятностного моделирования движения частицы во вращающейся системе координат.
Пользуясь такой моделью при известных значениях вероятностей pi , можно с помощью методов вероятностно-статистического моделирования и генератора случайных чисел моделировать движение частицы в закрученном потоке (рис. 1). Однако для использования его результатов для расчета поля концентраций частиц необходимо рассчитать большое количество случайных траекторий, учитывая и их различное положение в начальном сечении канала. Поэтому такой метод может использоваться для числа частиц не более нескольких сотен (рис. 2).
Детерминированная скорость u может быть представлена как отношение расстояния (1-k)ml, которое проходит частица за m перемещений и время mDt, к этому времени:
. (14)
Коэффициент диффузии для s-размерного случайного пути может быть определен по уравнению [10]:
, (15)
где`x = p1x1+p2x2+...+p2sx2s - средняя координата.
В соответствии с этим для вероятностно-статистического моделирования закрученного газодисперсного потока и расчета распределения частиц по сечению канала и его изменения по длине в каждом из уравнений вероятностно-стохастической модели появятся члены, отражающие влияние центробежной силы или детерминированной скорости движения частиц под действием центробежной силы [6]. Опуская достаточно очевидные рассуждения и преобразования, аналогичные осевому движению, основное уравнение модели для осесимметричного течения в канале в общем случае можно получить в виде
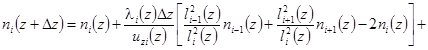
, (16)
где i = (R-r)/l - безразмерное расстояние от стенки канала (номер узла); l - интенсивность переходов (частота турбулентных пульсаций), с-1.
Если в качестве упрощающего допущения принять, что характеристики турбулентности (амплитуда и частота пульсаций) не изменяются по длине канала (li(z) = li и li(z) = li) и, кроме того, частота турбулентных пульсаций одинакова по сечению (li = l), то уравнение (16) примет вид
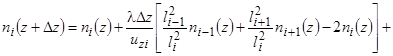
. (17)
Если в уравнениях движения частиц в радиальном направлении (3) и (9) пренебречь силой инерции, то в уравнении (17) скорость частиц uri можно оценить, приравняв силы аэродинамического сопротивления и центробежную силу. Тогда из уравнения (10)
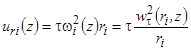. (18)
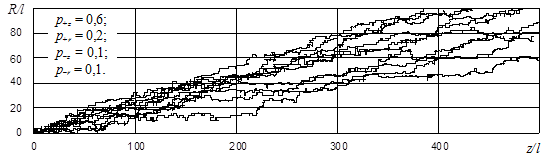
Рис. 2. Дискретное моделирование движения частиц в закрученном потоке
Тогда с учетом профиля тангенциальной составляющей скорости газа (12) для случаев, когда влиянием дисперсной фазы на поля скоростей газа можно пренебречь:
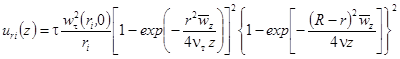. (19)
Расчеты по вероятностно-статистической модели показывают, что закрутка потока оказывает существенное влияние на поле концентраций частиц. Степень этого влияния зависит, в первую очередь, от размера (массы) и, соответственно, степени увлечения частиц турбулентными пульсациями газа. Для наиболее мелких частиц (диаметром менее 1-5 мкм в зависимости от плотности частиц, скорости и угла закрутки потока) с высокой степенью увлечения (b®1) закрутка потока только несколько ускоряет перераспределение частиц по сечению канала и делает его еще более неравномерным - концентрация частиц в пристенном слое становится более высокой, а вблизи оси – более низкой, чем в незакрученном потоке. По мере затухания крутки ее влияние на поле концентраций также слабеет и на достаточно большом расстоянии от входного сечения поле концентрации мелких частиц благодаря турбулентным пульсациям газа становится практически аналогичным равновесному профилю, характерному для осевого потока [6].
Наиболее крупные частиц (диаметром более 50-100 мкм в зависимости от плотности частиц, скорости и угла закрутки потока) с низкой степенью увлечения турбулентными пульсациями газа (b®0) благодаря закрутке потока достаточно быстро смещаются центробежной силой в периферийную область канала, и их концентрация в пристенном слое становится очень высокой, а вблизи оси – низкой. По мере затухания крутки ее влияние на поле концентраций слабеет, однако крупные частицы благодаря своей инерционности и малой степени увлечения очень медленно перераспределяются по сечению канала, и поле их концентрации сохраняется существенно неравномерным.
Частицы средних размеров (от 1-5 до 50-100 мкм) обладают достаточной массой и относительно низкой степенью увлечения, поэтому, с одной стороны, под воздействием центробежной силы перемещаются в периферийную зону, что приводит к значительной неравномерности их концентрации по сечению канала, однако, с другой стороны, после затухания крутки турбулентные пульсации газа приводят к постепенному перераспределению частиц по сечению, и в конце концов профиль их концентрации принимает равновесную форму, характерную для незакрученного потока, при котором в ядре потока частицы распределены практически равномерно с резким увеличением в пристенной зоне (рис. 3).
С использованием предложенного вероятностно-статистического подхода разработана модель движения дисперсных частиц в закрученном потоке газа с учетом влияния турбулентных пульсаций, позволяющая рассчитать профиль концентрации частиц и его изменение по длине и радиусу канала [3].
Рис. 3. Изменение профиля концентрации частиц в закрученном потоке: D = 50 мм, wz0 = 30 м/с, g = 60o, d = 3 мкм, rd = 3500 кг/м3
Рецензенты:
Хакимзянов Гаяз Салимович, доктор физико-математических наук, профессор, ведущий научный сотрудник, Институт вычислительных технологий СО РАН, г. Новосибирск.
Чекалов Лев Валентинович, доктор технических наук, генеральный директор ЗАО «Кондор-Эко», Ярославская область, п. Семибратово.