В настоящее время применение аппаратов вспомогательного кровообращения (ВК) и искусственного сердца (ИС) является одним из наиболее радикальных методов лечения сердечной недостаточности. Для этих целей применяются как экстракорпоральные, так и имплантируемые системы механической поддержки кровообращения, построенные на базе мехатронных модулей (ММ). Элементом ММ, в обоих типах указанных систем, непосредственно отвечающим за перекачивание крови, является искусственный желудочек сердца (ИЖС) объемного или роторного типа. Исходя из функционального назначения ИЖС, к его конструкции предъявляется ряд требований по гемодинамике. ИЖС не должен содержать зон застоя, рециркуляции потоков крови, турбулентности и т.д. Мембрана не должна касаться корпуса [3]. При работе ИЖС должен обеспечивать допустимый уровень гемолиза, который связан с повышенными касательными напряжениями, возникающими при рециркуляции крови в турбулентном потоке [2]. Высокая интенсивность касательных напряжений в турбулентных потоках вызывает разрушение форменных элементов крови – эритроцитов и активацию тромбоцитов, что приводит к формированию сгустка и тромбозу [5; 8; 9]. Серьезность наносимых повреждений элементам крови касательными напряжениями чрезвычайно высока и зависит как от их величины, так и от продолжительности их воздействия. Кроме взаимосвязи касательных напряжений и процесса тромбообразования, установлено, что формированию тромбов могут способствовать изменения скорости потока и его отсутствие (наличие застойных областей) в отделенных областях ИЖС [7].
Накопленный опыт отечественных и зарубежных ученых по проектированию систем ВК и ИС, с одной стороны, и имеющийся математический аппарат дают возможность прогнозировать поведение крови внутри камеры ИЖС и минимизировать указанные процессы на этапе проектирования, что позволит получать конструкции ММ ИС и ВК с заданными гемодинамическими параметрами.
Для прогнозирования поведения крови внутри камеры ИЖС и определения уровня гемолиза авторами предлагается использовать пакет конечно-элементного анализа - ANSYS 13.0 и его специализированное приложение для анализа гидродинамики FLOTRAN.
Основными уравнениями, описывающими течение несжимаемой ньютоновской вязкой жидкости, являются: уравнение неразрывности
![]() (1)
(1)
и уравнения движения сплошной среды (уравнения Навье-Стокса):
![]()
![]() (2)
(2)
![]()
где ux, uy, uz – составляющие (проекции) вектора скорости U; Р – давление; µ – эффективная динамическая вязкость; ν – кинематическая вязкость; ρ – плотность;
X, Y, Z – составляющие (проекции) вектора F внешней массовой силы; ∆ – оператор Лапласа.
Турбулентные течения характеризуются флуктуациями поля скорости. При решении уравнений Навье-Стокса, описывающих такие течения, применяется подход, основанный на использовании осредненных по времени величин. В результате появляются дополнительные неизвестные. Для замыкания системы уравнений используются различные модели турбулентности. Однако ни одна из известных моделей не является универсальной для всех существующих классов исследовательских задач. Выбор оптимальной модели турбулентности зависит от типа течения, специфического класса задачи, требуемой точности решения, доступных вычислительных ресурсов и т.п. Из многообразия общепризнанных моделей турбулентности можно выделить k-ε модель. k-ε модель является, видимо, наиболее удачной моделью турбулентности первого уровня замыкания. Для описания турбулентных величин в ней используется система двух нелинейных диффузионных уравнений – для кинетической энергии турбулентности (turbulence kinetic energy) – k (3) и для скорости диссипации турбулентной энергии (dissipation rate of turbulence energy) – ε (4).
![]() (3)
(3)
![]() , (4)
, (4)
здесь ![]() ,
,
![]() ;
; ![]() ,
,
где μt – турбулентная динамическая вязкость; μlam – динамическая вязкость ламинарного потока. C1ε, C2ε , Cμ , σε, σk – эмпирические константы k-ε модели турбулентности, имеющие следующие значения C1ε = 1,44; C2ε = 1,92; Cμ = 0,09; σε = 1,3; σk = 1 [6].
Гидродинамический анализ поведения крови в объеме ИЖС выполнен со следующими допущениями: жидкость не испытывает фазовых переходов; не учитываются массовые силы (силы гравитации); не рассматривается теплообмен со стенками камеры и в потоке жидкости; течение жидкости является турбулентным.
Граничные условия определяют значения искомых функций на границах потока и зависят от типа границ:
- неподвижная непроницаемая стенка, скорость движения жидкости на которой равна нулю, то есть реализуется условие «прилипания» жидкости к стенке;
- подвижная непроницаемая стенка, скорость движения жидкости на которой равна скорости движения стенки;
- свободная поверхность, на которой задается одно из значений искомых функций: скорость движения жидкости, давление жидкости.
Расчетная модель ИЖС пульсирующего типа с учетом влияния геометрии, действия клапанов, входных и выходных магистралей и движения мембраны создавалась на основе твердотельных моделей, разработанных в CAD-системе Pro/ENGINEER WF5 (рис. 1а). Исходная расчетная твердотельная модель представляет собой внутренний объем ИЖС с учетом реальной геометрии основного тела, клапанов, радиусов и переходов. Для создания конечно-элементной (КЭ) модели ИЖС использовался 8-узловой элемент FLUID 142, предназначенный для решения задач тепло-, массообмена и взаимодействия «жидкость – твердое тело», то есть для решения сопряженных задач. Для получения более точного решения разбиение происходило с учетом геометрической сложности объема и характера протекающих процессов. Это выражалось в сгущении сетки КЭ в зонах с высокими градиентами гидродинамических параметров (скорости, давления и т.п.) и сложной геометрии, определяющей характер течения (торможение, закрутка потока и т.п.). Сгущение выполнено в зонах клапана, патрубка, входа в ИЖС (рис. 1б). В соответствии с постановкой задачи в расчете использовалась только геометрия, участвующая в работе соответствующего цикла.
|
|
|
|
а) |
б) |
Рис. 1. Модели: а) 3D-модель ИЖС; б) КЭ модель внутреннего объема ИЖС
На входе потока жидкости в фазе диастолы и на выходе в фазе систолы задавалось нулевое значение избыточного давления. На остальных стенках ИЖС, клапана и патрубков задавались условия «прилипания» жидкости к стенке, то есть U = 0.
Использование подвижной стенки подразумевало нестационарную постановку задачи. Временные интервалы фаз диастолы и систолы были приняты из соотношения Тс / Тд = 1:3, частота сокращений кровяного насоса составила 1 Гц. В процессе решения интервал разбивался на 25 шагов с дискретностью 0,01 и 0,03 секунды соответственно. Параметры, характеризующие расчетную модель, представлены в табл. 1 [1].
Таблица 1
Параметры модели для гидродинамического анализа
|
Статистика КЭ модели |
|
|
Количество узлов |
179485 |
|
Количество элементов |
1011095 |
|
Тип элемента |
FLUID 142 |
|
Вид элемента |
3D, 8-узловой |
|
Средняя длина ребра, мм |
2 |
|
Средняя длина ребра в зонах сгущения, мм |
0,7 |
|
Параметры жидкости |
|
|
Динамическая вязкость, Па·с |
0,0032 |
|
Плотность, кг/м3 |
1060 |
|
Краевые условия |
|
|
Скорость движения мембраны, мм/с (м/с) |
10,5 / 21 (0, 105/0,21) |
|
Частота пульсаций мембраны, Гц |
1 |
|
Соотношение систола/диастола |
1:3 |
|
Время систолы, с |
0,25 |
|
Время диастолы, с |
0,75 |
|
Расход, л/мин |
5 |
|
Давление на выходе из ИЖС (артериальное), мм. рт. ст. (МПа) |
110 (0,02) |
|
Давление на выходе из ИЖС (венозное), мм. рт. ст. (МПа) |
10 (1,33х10-3) |
|
Ход мембраны, мм (м) |
±10 (± 0,01) |
Результаты численного моделирования гидродинамических процессов, протекающих внутри камеры ИЖС, представлены в виде контурных и векторных диаграмм, а также графиков, полученных в постпроцессоре ANSYS. Такое представление результатов является наиболее информативным и дает возможность визуально оценить изменение гидродинамических показателей. Диаграммы изменения гидродинамических параметров представлены по фазам и в порядке, соответствующем фазам сердечного цикла.
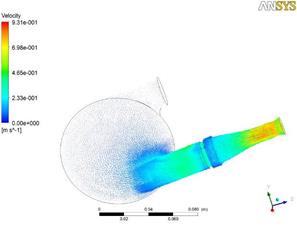
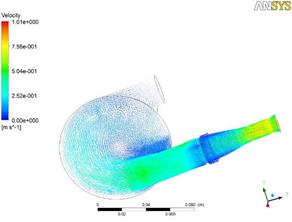
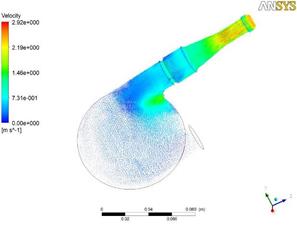
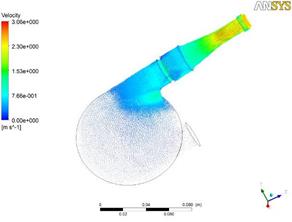
На рис. 2 представлены векторные диаграммы поля скоростей на общем виде ИЖС, для оценки наличия застойных зон, их размера и расположения внутри камеры ИЖС, а также зон закручивания потока, максимального значения скорости потока во время работы ИЖС. Данные представлены для начала и конца фазы диастолы и систолы соответственно.
Анализ приведенных диаграмм показывает отсутствие застойных зон, зон закручивания потока. Отличие между максимальными (1,01 м/с; 3,06 м/с) и минимальными (0,93 м/с; 2,92 м/с) значениями скорости потока крови для обеих фаз сердечного цикла составляет 1,1 раза. Минимальные значения скорости наблюдаются в начале фаз и достигают максимума по мере развития процессов заполнения или изгнания крови из камеры ИЖС.
|
|
|
|
а) |
б) |
|
|
|
|
в) |
г) |
Рис. 2. Поля векторов скоростей внутри камеры ИЖС: а), б) – в фазу диастолы; в), г) – в фазу систолы
В конце фазы диастолы наблюдается явное закручивание потока в сторону выходного патрубка. Максимальное значение скорости потока в начале фазы диастолы наблюдается на входе в патрубок и с течением времени перемещается в зону впускного клапана, где создается завихрение потока, которое может привести к травме форменных элементов крови и незначительному повышению уровня гемолиза, который будет компенсирован организмом.
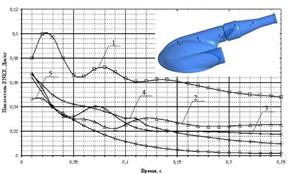
Не менее важным показателем, который оказывает влияние на поведение крови внутри камеры ИЖС и влияет на уровень гемолиза, является показатель ENKE. Данный показатель характеризует изменение турбулентных явлений.
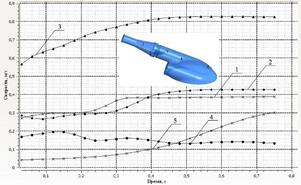
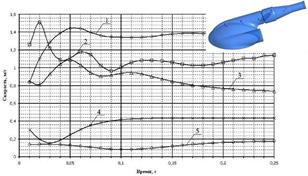
Для подтверждения отсутствия изменения значений скорости потока в большом диапазоне значений представлены графики изменения скорости потока крови и показателя ENKE в пяти характерных точках, лежащих внутри камеры ИЖС: конусная часть патрубка (1); диск открытого клапана (2, 3); область перехода цилиндрической части в основное тело ИЖС (4) и в области пересечения плоскости, проходящей через ось патрубка и основного тела ИЖС.
|
|
|
|
а) |
б) |
|
|
|
|
в) |
г) |
Рис. 3. Изменение скорости потока и показателя ENKE внутри камеры ИЖС: а), б) – в фазу диастолы; в), г) – в фазу систолы
Представленные кривые отражают стабильность процессов, протекающих во время систолы и диастолы в камере ИЖС, имея лишь всплески в начальный момент времени, которые объясняются неустановившимся процессом. Кривые имеют качественное сходство, отличаясь лишь абсолютными значениями. Исследуемые величины не меняют знак, а абсолютное значение колеблется в минимальном диапазоне, что не вызывает травм крови. Рассчитанный по известной методике [4] нормализованный индекс гемолиза (NIH) составил 0,0037 г/100 л, что хорошо коррелирует с аналогичным показателем отечественных и зарубежных систем, применяемых в различное время в клинической практике (рис. 4).
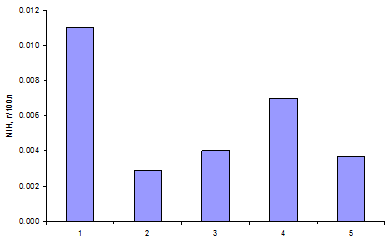
Рис. 4. Показатель NIH для различных конструкций ИЖС:
1 – ИЖС «Ясень» с клапаном типа «ЭМИКС»;
2 – центрифужный насос «CentriMag®»;
3 – центрифужный насос «Medtronic BP-80»;
4 – центрифужный насос «GYRO®»;
5 – разработанная конструкция ИЖС
Рецензенты:
Гоц А.Н., д.т.н., профессор, профессор кафедры тепловых двигателей и энергетических установок ФГБОУ ВПО «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых», г. Владимир.
Житников Б.Ю., д.т.н., профессор кафедры специальной техники и информационных технологий, заместитель начальника по научной работе ФКОУ ВПО «ВЮИ ФСИН» России, г. Владимир.