При разработке мер по снижению шума круглых пил важно знать соотношение между шумом, возникающим от вибрации пильного диска, и шумом от упругих деформаций перерезанных волокон древесины в зоне резания.
Цель настоящей работы – дать теоретический анализ излучения звука (шума) дисковой пилой под действием сил резания.
Диск пилы представляет собой однородную изотропную круглую пластину, ограниченную двумя концентрическими окружностями с радиусами r0 и r1.
Уровень звуковой мощности, излучаемый источником с заданным распределением колебательной скорости, записывается [2]:
, дБ, (1)
где 
– уровень звуковой мощности (относительно 10-12 Вт), дБ;
– средний по площади пилы уровень колебательной скорости (относительно 5*10-8 м/с);
– площадь поверхности излучения (диска пилы), м2;
– коэффициент излучения.
Основной вклад в формирование звукового поля вносят изгибные колебания пилы.
Уравнение движения диска пилы в цилиндрических координатах под действием внешней силы запишется [1; 4]:
, (2)
где 
– цилиндрическая жесткость пилы на изгиб;
– модуль упругости материала;
– толщина диска пилы;
– коэффициент Пуассона;
– мнимая единица;
– коэффициент потерь;
– прогиб срединной плоскости пилы;
– вес единицы площади диска пилы;
– текущая радиальная и угловая координаты точки диска пилы;
– интенсивность внешней нагрузки;
– двойной оператор Лапласа в полярных координатах .
Граничные условия на внутреннем радиусе диска пилы (в месте крепления его зажимными шайбами) при r = r0 можно представить в виде жесткого закрепления внутреннего контура: 
;
.
Граничные условия на внешнем контуре в процессе пиления будут постоянно меняться от свободных колебаний (как происходит при холостом ходе пилы) до шарнирно-опертого контура и даже до жестко закрепленного контура.
Эти граничные условия можно представить в виде:
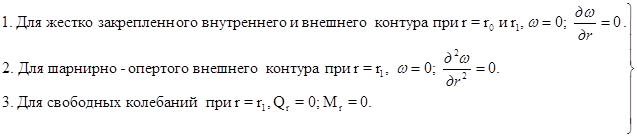, (3)
Решение уравнения (2) будем искать в виде разложения в ряд по фундаментальным функциям, соответствующим формам собственных колебаний диска пилы.
Представим решение однородного уравнения
, (4)
в виде:
,
где 
– частота собственных колебаний пилы;
и 
– неизвестные функции только ;
и 
– постоянные.
Внесем 
в уравнение (4). Получим:
. (5)
Обозначим:
.
Получим систему двух уравнений:
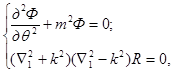(6) (7)
где
,
где 
– число узловых диаметров.
Решая уравнение (6) и удовлетворяя граничным условиям (3), найдем:
, (8)
где 
,
– постоянная величина.
Общее решение уравнения (7) запишется:
, (9)
где 
, 
– функции Бесселя m-го порядка первого и второго рода соответственно;
, 
– функции Бесселя мнимого аргумента;
– число условных окружностей.
Постоянные 
, 
, 
, 
и 
для данного m определяются из граничных условий. Удовлетворение граничным условиям приводит к частотному уравнению, из которого для заданного числа узловых диаметров m определяется бесчисленное множество корней 
.
Общее решение однородного уравнения (4) запишется в виде
. (10)
Постоянные 
и 
определяются из начальных условий. Перейдем теперь к интегрированию основного дифференциального уравнения (2). Нагрузку, действующую на диск пилы в первом приближении, можно аппроксимировать действием периодических импульсов с периодом Т0 (рис.1): 
,
где 
, (11)
– число оборотов диска пилы в минуту;
– число зубьев пилы.
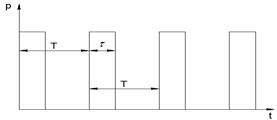
Рис. 1. График изменения нагрузки во времени
Для получения условия ортогональности в уравнении (7) сделаем замену переменных (2):
, 
. (12)
Это дает:
. (13)
Пусть 
и 
являются решениями уравнения (13) при данном числе узловых диаметров. Тогда можно записать:
и
.
Умножив первое равенство на , второе на , вычтя из первого второе и интегрируя по x в пределах от 
до 
, получим:
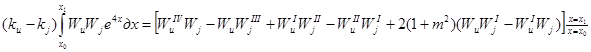. (14)
Возвращаясь к переменной r и функции R(r), с учетом граничных условий найдем:
.
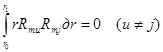Это есть условие ортогональности функций 
. Разделим (14) на 
и перейдем к пределу при 
. Тогда получим с учетом граничных условий:
.
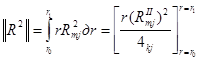Решение уравнения (2) будем искать в виде:
. (15)
Разложим нагрузку в двойной ряд по функциям 
и 
. Ортогональность этих функций доказана, поэтому такое разложение возможно:
.
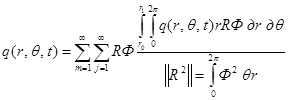Подстановка этого ряда в уравнение (2) дает нам следующее уравнение для нахождения 
:
, (16)
где
;
.
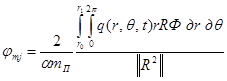При нагрузке в виде импульсов целесообразно применение операционного метода решения [2; 3]. При помощи единичной функции
график нагрузки записывается в виде:
.
Поэтому:
. 
,
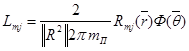где 
и 
– координаты точки приложения импульсов.
Пусть начальные условия будут:
.
Изображение уравнения (16) запишется в виде:
, (17)
где 
– оператор Лапласа.
Нас интересует не полное решение уравнения (16), а лишь его периодическая часть, для которой 
и соответствующее установившимся чисто вынужденным колебаниям. Для отыскания периодического решения нужно так определить 
, чтобы начальная функция 
обращалась тождественно в нуль при 
, где:
;
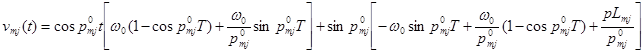Отсюда имеем:
; 
.
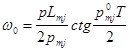Подставляя значение и 
в уравнение (17) и находя начальную функцию v(t) при 0< t<T, получим искомое периодическое решение:
.
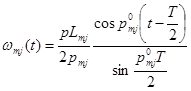Выражение для скоростей чисто вынужденных колебаний пилы под действием периодических импульсов запишется:
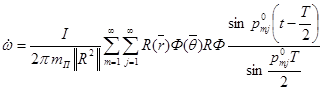, (18)
Средние значения квадратов абсолютных величин скоростей смещений диска пилы за промежуток времени между двумя импульсами сил при частоте колебаний 
подставляем в формулу (1). Избавляясь от величин 
и 
способом В.И. Заборова [2], заменив массу единицы площади произведением 
(
- плотность материала диска пилы), получим величину уровня звуковой мощности, излучаемой пилой на частоте 
:
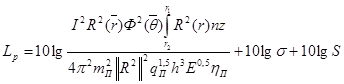, дБ. (19)
Хотя в замкнутом виде получить абсолютные значения излучаемой звуковой мощности пилой на частоте fмn из-за сложности математического аппарата по определению колебательной скорости не удалось, анализ уравнения (19) позволяет сделать некоторые важные выводы.
Как видно из формулы (19), для двух пил с одинаковыми размерами в плане основное значение для излучения шума пилой имеет толщина пилы. Увеличение толщины пильного диска в 2 раза дает снижение уровня шума примерно на 9 дБ.
Снижение числа зубьев пилы в 2 раза приводит к снижению уровня шума на 3 дБ. Такого же снижения уровня можно добиться увеличением коэффициента потерь в 2 раза и снижением скорости резания.
Влияние площади поверхности пилы на излучаемую звуковую мощность подтверждает полученную ранее зависимость в работе [5]: изменение площади в 2 раза дает изменение уровня звука на 3 дБ.
Слагаемое 
в формуле (19) определяет механизм перехода вибраций диска в акустическую энергию шума.
Влияние этого слагаемого требует дополнительного самостоятельного исследования и составляет предмет следующей статьи.
Рецензенты:
Санников Александр Александрович, доктор технических наук, профессор, заведующий кафедрой «Машины и оборудование целлюлозно-бумажного производства» ФГБОУ ВПО «Уральский государственный лесотехнический университет», г. Екатеринбург.
Пашков Валентин Кузьмич, доктор технических наук, профессор кафедры «Станки и инструменты» ФГБОУ ВПО «Уральский государственный лесотехнический университет», г. Екатеринбург.