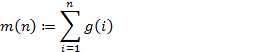Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

Вузовский курс математики, преподаваемый студентам технических и экономических специальностей и направлений подготовки, предусматривает изучение теории вероятностей. Понимание вероятностных явлений и процессов всегда вызывает определенные трудности у студентов, так как их познание связано с постижением гносеологического смысла случайного и необходимого. Изучение теоретического материала начинается с формирования математического понятия вероятности события, определяемого несколькими способами. Согласно классическому определению, вероятностью Р(А) события А называется отношение числа случаев m, благоприятствующих ему, к общему числу случаев n (P(A) = m/n) [1; 2; 4]. Отношение числа испытаний m, в которых событие А происходит, к общему числу испытаний n называется относительной частотой w(A) этого события или статистической вероятностью (w(A) = m/n) [1; 2; 4]. Если испытания будут независимыми, повторными и проводимыми в одинаковых условиях, то вероятность наступления события, выступающего результатом их осуществления, сохраняет свое значение р, а относительная частота m/n изменяется и отличается от р. Утверждения о соотношении величин m/n и р устанавливаются из следствия интегральной теоремы Муавра–Лапласа и теоремой, сформулированной Я. Бернулли (1654–1705). Освоение студентами содержания понятия вероятности события во многом определяет успешность изучения последующих тем «Случайные величины» и «Закон больших чисел», поэтому представляется целесообразным уделить должное внимание решению такой методической проблемы, как иллюстрация соотношения величин m/n и р.

Опытная проверка приближения относительной частотой m/n к вероятности p осуществлялась на начальных этапах развития теории вероятностей средствами натурного эксперимента. В учебной литературе приводятся сведения о том, что естествоиспытатель Ж. Бюффон (1707–1788) и математик К. Пирсон (1857–1936) многократно подбрасывали монету и фиксировали результаты выпадения одной, заранее выбранной стороны [2; 4]. Представляется логичным при изложении учебного материала о независимых повторных испытаниях использовать наглядную иллюстрацию стремления относительной частоты события m/n к ее вероятности p, так как многие студенты проявляют, прежде всего, интерес к практическому использованию знаний вероятностных закономерностей.

Любая денежная монета, как известно, имеет две стороны, на одной из которых отмечен ее номинал, а на другой – государственная символика. Вероятность выпадения какой-либо одной стороны монеты равна 1/2, так как она симметрична относительно своих сторон. Результаты экспериментов Ж. Бюффона и К. Пирсона [2; 4] представлены в таблице 1.

Таблица 1

Результаты натурного эксперимента

Повторить исторически известные натурные эксперименты Ж. Бюффона и К. Пирсона в учебном процессе достаточно затруднительно, так как их постановка требует больших временных затрат, но при современном развитии вычислительной техники становится возможным их имитационное моделирование [6; 7].

Построение дидактического сопровождения применения вычислительного эксперимента, адекватно отображающего независимые повторные испытания, при формировании у студентов понятия вероятности события, выступает целью данного исследования.

Результаты и обсуждение

Отбор учебно-теоретического материала. При постановке независимых повторных испытаний интерес представляет тот факт, что некоторое событие А в отдельно взятом опыте может наступить или не наступить, но в результате серии опытов оно непременно появляется определенное количество раз. Современная формулировка теоремы Я. Бернулли утверждает, что если производится n независимых испытаний, в каждом из которых событие А может появиться с постоянной вероятностью р (0 < p < 1), то вероятность того, что относительная частота m/n появления события А удовлетворяет неравенству и становится сколь угодно близкой к единице при достаточно большом количестве испытаний [5]. Я. Бернулли доказал эту теорему средствами «чистой математики». Известный математик последние двадцать лет своей жизни посвятил исследованию проблем теории вероятностей, но его труд «Искусство предположений», который включал отмеченную выше теорему, вышел в незавершенном виде только в 1713 г. уже после смерти автора [5].

Теорема Я. Бернулли в настоящее время входит в группу теорем, которая получила название закона больших чисел. Знакомство с этой группой теорем отделено во времени от изучения независимых повторных испытаний, поэтому у студентов не формируется целостного представления об условиях приближения относительной частотой появления события к его относительной мере возможного наступления (m/n → p) на этапе формирования понятия вероятности события.

В следствии из интегральной теоремы Муавра–Лапласа [1; 2; 4], которым завершается изучение независимых повторных испытаний в рамках дисциплины «Математика», рассматривается утверждение о том, что если при каждом из n независимых испытаний вероятность появления некоторого случайного события А равна р (0 < р < 1), а m – число испытаний, в которых А фактически наступает, то для определения вероятности осуществления неравенства при заданном числе ε > 0 используется приближенное равенство

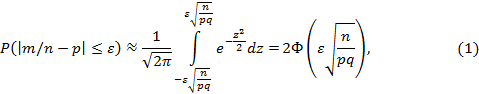
где Φ(х) – функция Лапласа, вычисляемая по формуле

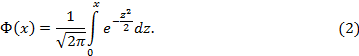
Формула (1) раскрывает соотношение относительной частоты m/n события А с его вероятностью p, отображая дуалистическое единство статистического и классического определений понятия вероятности события. Функция Лапласа Ф(х) задается таблично для аргумента Если , то значение Ф(х) находится по формуле , так как функция Лапласа обладает свойством нечетности. Если , то Ф(х) принимается равной 1/2, следовательно, 2Ф(х) становится равной единице. Если 2Ф(х) ≈ 1, то это означает достоверность того, что относительная частота m/n отличается от вероятности p на величину ε, значение которой связано с количеством испытаний n.

Конструирование имитационной модели. Имитацией подбрасывания монеты может выступать работа генератора случайных чисел. Если генерируются равномерно распределенные случайные числа, значения которых принадлежат интервалу [0; 1], то интервалы [0; 0,5) и [0,5; 1] могут моделировать две стороны монеты. Подсчет чисел, которые попадают в интервал [0,5; 1], удобно осуществлять с помощью операции суммирования, предварительно округляя каждое значение до целого (каждое число преобразуется в единицу). При округлении значений до целого преобразуются в ноль числа, которые принадлежат интервалу [0; 0,5). Отбор непрерывных случайных величин, имеющих значения от 0 до 1, с помощью округления до целого однозначно устанавливает количество данных, попадающих только в один интервал.

Составление программы вычислений. Система компьютерной математики MathCAD [3], которая активно используется студентами при изучении вузовского курса математики, позволяет осуществить имитационное моделирование независимых повторных испытаний, проводимых Ж. Бюффоном и К. Пирсоном. Рассмотрим эксперимент, моделирующий выпадение орла при подбрасывании монеты. Выпадению номинала монеты в этом случае будет соответствовать случайное число, принадлежащее интервалу [0; 0,5). Выпадению орла – случайное число, принадлежащее интервалу [0,5; 1]. Отклонение значений относительной частоты m/n выпадения орла от вероятности р = 0,5 для заданного количества испытаний n удобно наблюдать на графике, отображающем соответствующие величины. Сопоставление теоремы Бернулли и формулы (1) приводит к построению выражения , которое означает, что выполнение неравенства можно рассматривать как практически достоверное событие Р(|m/n – p| ≤ ε) → 1, если известно ε.

Значение ε при заданном значении функции 2Ф(х) рассчитывается по формуле

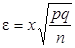, (3)

Выбор значения 2Ф(х), близкого к единице, позволяет исследовать достоверность покрытия относительной частоты m/n выпадения орла интервалом [0,5 – ε; 0,5 + ε]. В библиотеку статистических функций системы MathCAD [3] входит функция dnorm (x, a, σ), использование которой позволяет составить функцию P(x) = 2Ф(х), имеющую следующий вид:

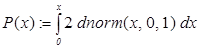, (4)

где функция dnorm(x, 0, 1) соответствует функции.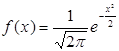

Целенаправленный выбор значений функции Р(х) (вероятности покрытия значения m/n интервалом [0,5 – ε; 0,5 + ε]) для расчета ε удобно осуществлять, имея графическое представление функциональной зависимости. Построить график функции Р(х) в системе MathCAD [3] можно с помощью оператора двумерного графика (рис. 1).

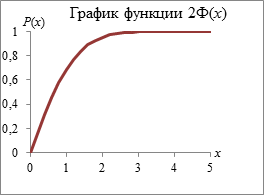
Рис. 1. График функции Р(х)

Программа для имитационного моделирования опытов Ж. Бюффона и К. Пирсона по подбрасыванию монеты представлена в таблице 2, а значения вычисляемых величин отражены на рис. 2.

Таблица 2

Программа «Иллюстрация значений относительной частоты независимых повторных испытаний (имитация бросания монеты)»

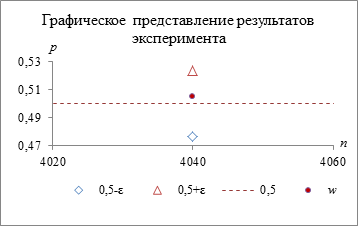
Рис. 2. Имитационное моделирование опыта Ж. Бюффона

Работа программы для проведения вычислительного эксперимента запускается введением следующих начальных данных: 1) количество испытаний n; 2) вероятность выпадения орла р; 4) значение аргумента х. Функция rnd (1) создает одномерный массив чисел, равномерно распределенных в интервале от 0 до 1. Переменная i определяет объем массива (количество генерируемых чисел). Функция round (х, 0) округляет значение полученных чисел точностью до целого, то есть преобразует их в дискретную величину, имеющую значение или 0 или 1. Оператор ∑ выполняет суммирование единиц. Функции пользователя ε(n), l1(n) и l2(n) находят соответственно значение ε и значения нижней и верхней границ интервала [р – ε; р + ε].

Анализ и интерпретация полученных результатов. Функция 2Ф(х) монотонно возрастает на интервале от 0 до 3 и существенно не изменяется на интервале от 3 до 5. Выберем для проведения учебного имитационного эксперимента значение 2Ф(3), равное 0,9973. В этом случае ε, рассчитанное по формуле (3), для опыта Ж. Бюффона примет значение 0,024, а для опытов К. Пирсона – 0,014 и 0,010 соответственно. Вывод на демонстрационный экран рабочего пространства системы MathCAD в учебной аудитории, оснащенной мультимедиаоборудованием, позволяет при использовании данной программы наблюдать на графике значения границ интервала [р – ε; р + ε] (обозначены ромбом и треугольником), значение относительной частоты w(A) выпадения орла (обозначено кружком), вероятности р выпадения орла (пунктирная линия).

Следует отметить, что количество выпадений орла в имитационном эксперименте, равное 2041 (рис. 2), не совпадает с результатом, полученным Ж. Бюффоном (табл. 1). Относительные частоты выпадения орла 0,507 и 0,505 (соответственно рассчитанные по данным натурного и имитационного эксперимента) при заданном условии P(|m/n – 0,5| < 0,024) = 0,9973 покрываются интервалом [0,476; 0,524]. Если переменной n присвоить значения 12000 или 24000, то можно успешно провести имитационное моделирование опытов К. Пирсона. Учитывая, что вероятностные закономерности в единичных испытаниях проявляются по-разному и только их многократное повторение позволяет «увидеть» их некоторую устойчивость, представляется целесообразным провести имитационное моделирование опытов Ж. Бюффона и К. Пирсона несколько раз и зафиксировать полученные данные. Собранный эмпирический материал позволяет организовать со студентами обсуждение вероятностных закономерностей и предложить им провести подобные исследования при других значениях функции 2Ф(х) или при других значениях n. Завершить изучение независимых повторных испытаний можно в процессе беседы об изменениях длины задаваемого интервала и отклонений m/n от р = 0,5 для различных значений n при условии 2Ф(3) = 0,9973 (рис. 3).

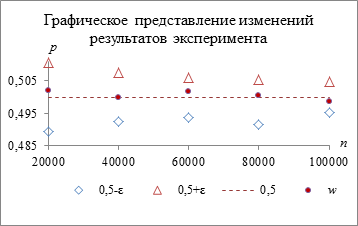
Рис. 3. Изменение длины интервала [0,5 – ε; 0,5 + ε]

Увеличение количества имитаций подбрасываний монеты до 100000 приводит к существенному уменьшению интервала [0,5 – ε; 0,5 + ε] (рис. 3), что означает более значимое уменьшение отклонения m/n от 1/2 по сравнению с величиной отклонений, когда . Отмеченная тенденция хорошо иллюстрирует утверждение теоремы Я. Бернулли.

Заключение

Последовательное выполнение таких действий, как отбор учебно-теоретического материала, конструирование имитационной модели, составление программы вычислений, анализ и интерпретация полученных результатов, позволяют успешно достигнуть поставленной цели. Представленное дидактическое сопровождение методически адаптировано для его использования студентами при изучении теории вероятностей в вузовском курсе математики. Визуализация функциональных зависимостей и значений исследуемых величин средствами системы компьютерной математики MathCAD выступает одним из вариантов решения отмеченной выше методической проблемы иллюстрации соотношения величин m/n и р. Включение предлагаемых материалов в учебный процесс направлено на создание благоприятных условий для восприятия и осознания вероятностных закономерностей.

Рецензенты:

Туранов Х.Т., д.т.н., профессор Уральского государственного университета путей сообщения (УрГУПС), г. Екатеринбург.

Казанцева Н.В., д.ф.-м.н., старший научный сотрудник Института физики металлов УрО РАН, г. Екатеринбург.