Введение
Необходимость поиска символьных выражений возникает при решении разнообразных задачи синтеза управления. Синтез системы управления состоит в построении управления в виде функции от координат пространства состояний объекта. Аналитические методы синтеза систем управления применимы только к узкому классу систем. Одна из основных причин сложности аналитического поиска многомерной функции управления состоит в том, что она, как правило, имеет разрывы первого рода по значениям или производным.
В данной работе рассматривается приложение двух методов из области генетического программирования к задаче синтеза системы управления. Генетическое программирование (ГП) было предложено Дж. Козой в [7] в качестве метода поиска программ, отвечающих заданному критерию. ГП применялось для решения задачи синтеза системы управления роботом-тележкой [6].
В последнее время с целью усовершенствования ГП появились методы грамматической эволюции [8; 9], аналитического программирования [10] и сетевого оператора [1–5]. В работе рассмотрены методы грамматической эволюции и сетевого оператора как наиболее подходящие для решения задачи синтеза управления.
Одной из главных проблем в области ГП является выбор представления решений, подходящего как для задачи, так и для выбранного метода поиска. Для представления решения в методе сетевого оператора используется направленный ациклический граф. Такой граф называется сетевым оператором. Он может быть представлен в виде верхней треугольной матрицы специального вида, построенной на основе матрицы смежности. Такое представление особенно удобно для проведения вычислительных экспериментов, так как матричное представление является естественным для большинства современных языков программирования. Однако метод сетевого оператора не лишён и недостатков, в числе которых следует назвать отсутствие возможности использования при поиске функций арности выше двух и невозможность включения в символьную запись оператора условия.
В грамматической эволюции для построения символьного выражения используются принципы формальной грамматики. Грамматика языка выражения задаётся в виде системы продукционных правил в форме Бэкуса-Наура (БНФ). Грамматическая эволюция лишена недостатков, присущих методу сетевого оператора, однако символьные выражения, получаемые в процессе работы метода, требуют либо поддержки функции eval со стороны языка, либо написания интерпретатора под каждую новую задачу.
В данной работе сравниваются описанные методы применительно к задаче синтеза управления нелинейной системой. В качестве объекта управления выбрана пружина Дуффинга.
Постановка задачи синтеза системы управления
Задана модель объекта управления в виде системы обыкновенных дифференциальных уравнений:
(1)
где, в общем случае, 
— нелинейная векторная функция векторных аргументов 
, 
, где множество 
замкнуто и ограничено, 
.
Задано множество начальных условий
. (2)
Задано множество целевых значений
. (3)
Задан функционал качества управления
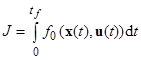, (4)
где
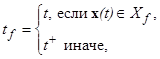(5)
и 
— заданная верхняя граница приемлемого времени управления.
Требуется найти функцию управления
, (6)
обеспечивающую минимум функционалу (4) и удовлетворяющую терминальным условиям
, (7)
и ограничениям на управление
, (8)
для 
системы (1).
В общем случае искомая функция управления (6) нелинейна и может иметь разрывы, что затрудняет или делает невозможным построение системы управления аналитическими методами.
Грамматическая эволюция
Грамматическая эволюция (ГЭ), предложенная в [9], объединяет принципы генетического программирования и формальной грамматики. Первой особенностью ГЭ, отличающей её от ГП, состоит в том, что она обрабатывает популяцию целочисленных хромосом, тогда как ГП работает с символьными S-выражениями. Хромосомы могут быть как бинарными, так и содержать числа в десятичной системе счисления. Хромосомы могут иметь произвольную или фиксированную длину. ГЭ — модульный алгоритм. Для поиска решения можно использовать любой алгоритм, способный работать с популяциями. В данной работе использовался стационарный генетический алгоритм.
Для преобразования хромосомы в символьное выражение используется система особым образом пронумерованных продукционных правил, заданных в форме Бэкуса-Наура. Эти правила описывают язык математического выражения. Для построения такой системы требуется ввести несколько множеств: 
— множество нетерминальных символов, 
— множество терминальных символов, 
— множество нетерминальных символов, один из которых выбирается в качестве стартовой символьной строки.
Рассмотрим следующий пример. Пусть задано простейшее алгебраическое выражение
. (9)
Тогда для построения системы продукционных правил, в соответствии с которыми можно вывести выражение (9), можно использовать следующие множества:
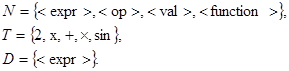(10)
На основе множеств (10) строим систему, состоящую из 
продукционных правил, число которых соответствует количеству элементов множества (таблица 1). Здесь символ “|” является обозначением оператора выбора между вариантами.
Таблица 1. Система продукционных правил для построения выражения (9).
|
№ правила |
Выражение |
Вариант |
№ варианта |
|
1 |
<expr> |
<expr> <op> <expr> | <function>(<expr>) | <val> |
0 | 1 | 2 |
|
2 |
<op> |
|
0 | 1 |
|
3 |
<val> |
|
0 | 1 |
|
4 |
<function> |
sin |
0 |
| 
| 
В столбце «Выражение» находится выражение, подлежащее замене, в столбце «Вариант» расположены возможные варианты замены для заданного выражения. Пронумеруем варианты в каждом правиле числами от 0 до 
, 
, где 
— число вариантов замены для 
-го правила.
Пусть задана целочисленная хромосома 
. Реконструировать символьное выражение возможно по следующему алгоритму.
1. Пусть 
— строка, содержащая символ из множества . Зададим 
.
2. Выберем самый левый нетерминальный символ 
в строке и определим номер правила в соответствии с этим символом.
3. Заменим 
на вариант замены с номером 
.
4. Если в нет нетерминальных символов и 
, то 
и переходим к п. 2; если в есть нетерминальные символы и 
, то применяем оператор обёртывания [9]; иначе построение символьного выражения завершено.
Одной из возможных хромосом для выражения (9) будет 
.
Метод сетевого оператора
Сетевой оператор [1–5] представляет собой ациклический ориентированный граф, который описывает некоторое математическое выражение. Для построения сетевого оператора вводятся четыре конечных упорядоченных множества: множество переменных 
, множество параметров 
, множество унарных операций 
и множество бинарных операций 
, причём бинарные операции должны обладать свойствами коммутативности, ассоциативности и иметь единичные элементы. Данный граф обладает следующими характеристиками: каждому узлу-источнику сопоставлен элемент из множеств или , каждой дуге графа сопоставлен элемент из множества , каждому узлу, не являющемуся источником, сопоставлен элемент из множества .
Сетевой оператор описывает несколько математических выражений, число которых равно числу узлов, не являющихся источниками. Обычно лишь часть таких узлов считаются «выходами» сетевого оператора.
Сетевой оператор может быть представлен в виде матрицы, построенной на основе матрицы смежности исходного графа. Матрица сетевого оператора 
имеет верхний треугольный вид.
Метод сетевого оператора успешно применялся для синтеза систем управления [1–5].
Вычислительный эксперимент
Рассмотрим задачу синтеза управления пружины Дуффинга. Модель объекта управления описывается следующей системой уравнений:
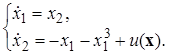(11)
Функция управления ограничена:
. (12)
Для выполнения ограничений (12) принимаем условия, что если в момент 
найденная функция 
, то 
, а если 
, то 
.
Таблица 2. Система продукционных правил, применявшаяся в методе ГЭ.
|
№ правила |
Выражение |
Вариант |
№ варианта |
|
1
|
<expr> |
(<expr>) <op> (<expr>) | <f1arg>(<expr>) |<val> |
0 | 1 | 2 |
|
2 |
<op> |
+ | – | |
0 | 1 | 2 | 3 |
|
3 |
<val> |
|
0 | 1 | 2 | 3 | 4 | 5 |
|
4 |
<f1arg> |
step | abs | sign | logist | absqrt | atan |
0 | 1 | 2 | 3 | 4 | 5 |
| 
| 
| 
| 
| 
Пусть начальными условиями для данной системы будет множество
, (13)
где 
, 
, 
, 
.
Для всех начальных условий целевым множеством будет
, (14)
где 
.
Будем искать функцию управления в соответствии с функционалами
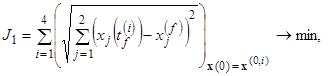(15)
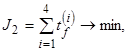(16)
где индекс 
означает, что система (11) интегрируется при начальном условии 
; 
задаётся в соответствии с (5); 
— время окончания моделирования для 
, а максимально приемлемое время 
с.
Алгоритм ГЭ был модифицирован. Основная модификация заключается в том, что в генетическом алгоритме использовался принцип коэволюции: помимо популяции, хранящей закодированные выражения языка, для которого заданы множества 
и система продукционных правил (таблица 2), генетический алгоритм обрабатывает также и популяцию числовых параметров, причём эти параметры входят в множество 
. Метод сетевого оператора использует аналогичный принцип: вместе с популяцией вариаций базисного решения обработке с помощью генетических операторов скрещивания и мутации подвергается и популяция параметров, относящихся к множеству .
Методом грамматической эволюции была найдена следующая функция управления:
где 
, 
— функция Хевисайда, 
.
Методом сетевого оператора была найдена следующая функция управления:
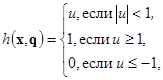
где
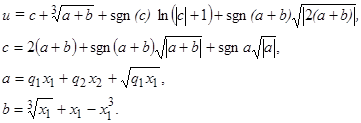
Здесь вектор параметров 
.
Функции управления в методах ГЭ, и сетевого оператора выбирались из множества Парето оптимальных решений.
Синтезированное рассматриваемыми методами управление затем проверялось на новом множестве начальных условий, которые не использовались для процесса поиска,
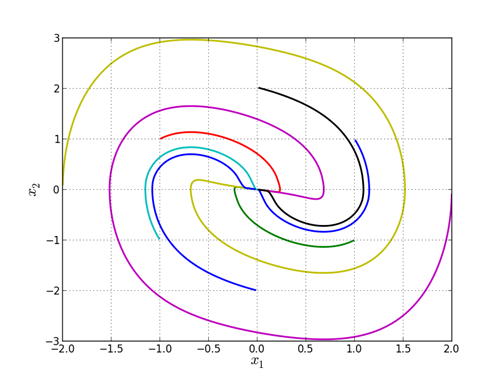
Результаты моделирования системы, полученной методом грамматической эволюции, приведены на рис. 1; результаты моделирования системы, полученной методом сетевого оператора, приведены на рис. 2.
Результаты моделирования показывают, что оба метода успешно синтезировали функцию управления, решающую задачу приведения системы в точку, то есть синтезированные управляющие функции обеспечивают решение задачи синтеза не только для тех точек, которые использовались при поиске управления, но и для других точек из определенной области.
Рис. 1. Фазовые траектории системы с управлением, полученным методом ГЭ, для множеств начальных условий 
и 
.
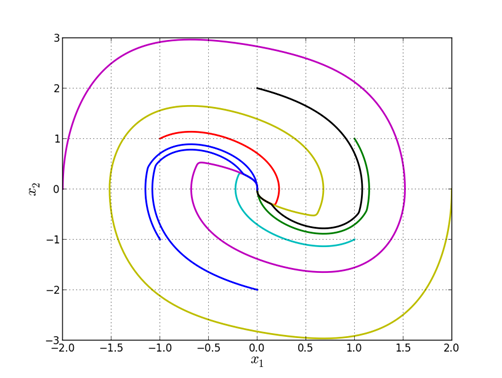
Рис. 2. Фазовые траектории системы с управлением, полученным методом сетевого оператора, для множеств начальных условий и .
Работа выполнялась по грантам РФФИ № 13-08-00523а и 11-08-00532а.
Рецензенты:
Дикусар В.В., д. ф. м. н., профессор, главный научный сотрудник ФГБУ «Вычислительный центр им. А.А. Дородницына» Российской академии наук, г. Москва.
Мочалов И.А., д. т. н, профессор, кафедра «Системы автоматического управления» (ИУ-1), Московский государственный технический университет им. Н.Э. Баумана, г. Москва.