В основу реализации технологии развивающего обучения теории вероятностей (ТВ) будущих учителей математики нами положены концепции профессионально-педагогической направленности обучения математике в вузе (Г.Л. Луканкин, А.Г. Мордкович, Л.В. Шкерина); общедидактические теории реализации идей развивающего обучения и деятельностного подхода к его организации (З.И. Калмыкова); методические теории усиления развивающих функций математического образования (В.А. Гусев, Г.С. Евдокимова, В.Д. Селютин); психологические теории мыслительной деятельности (Д.Н. Богоявленский, Р. Вудвордс, Н.А. Менчинская, С.Л. Рубинштейн и др.).
На основе этих концепций и теорий разработана методическая система ориентации обучения ТВ будущих учителей математики на развитие основных приемов мыслительной деятельности, которая схематически может быть представлена следующим образом (схема 1).
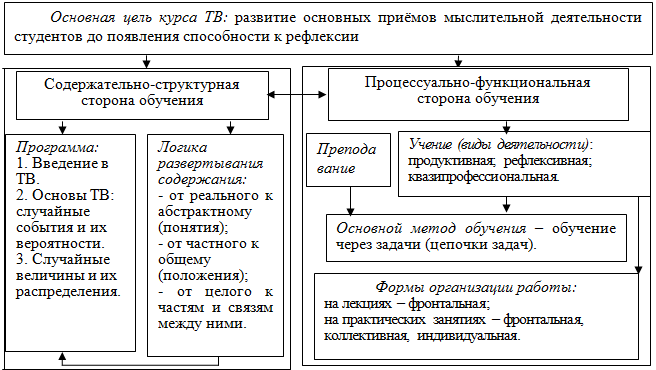
Схема 1. Методическая система обучения ТВ будущих учителей математики, ориентированного на развитие основных приемов мыслительной деятельности
Под развитием основных приемов мыслительной деятельности в рамках данного исследования понимается процесс образования комбинаций приемов анализа и синтеза с последующим усложнением этих комбинаций и установлением связей их с другими подсистемами мыслительной деятельности.
В качестве основного метода обучения в рамках представленной методической системы выступает особая модификация метода обучения через задачи – обучение через цепочки задач. Под цепочкой задач будем понимать последовательность задач, проводящих студентов через все уровни развития основных приемов мыслительной деятельности.
Разработанные нами цепочки задач состоят из четырех типов задач, соответствующих уровням развития основных приемов мыслительной деятельности и расположенных в порядке, соответствующем последовательной смене этих уровней.
1. Задачи на получение выводов о существенных свойствах основных понятий теории вероятностей и знаний о заключениях тех теорем, которые являются прямым следствием известных положений, или на распространение результатов статистического эксперимента на генеральную совокупность; обратные к ним задачи, т.е. задачи на восстановление посылок сделанных выводов, которые представляют собой утверждения о признаках понятий теории вероятностей и утверждений об их статистических аналогах. Постановка такого вида задач позволяет включать студентов в деятельность оперирования приемами «синтез» или «анализ».
2. Задачи, представляющие комбинацию задач первых двух типов, решение которых обеспечивает получение знаний о связях известных понятий и утверждений теории вероятностей, об идеях теории вероятностей и ее приложений (представление случайных событий в виде суммы и (или) произведения других случайных событий, переход к противоположному событию; вероятностная симметрия; представление случайных величин в виде функции других случайных величин; замена одних форм распределения случайных величин другими; использование закона больших чисел в различных формах и др.). Постановка такого вида задач позволяет включать студентов в деятельность оперирования различными комбинациями приемов анализа и синтеза («синтез через анализ» и «анализ через синтез»).
3. Задачи, решение которых требует привлечения поисковых аналитико-синтетических стратегий (восходящий анализ, анализ в форме расчленения, нисходящий анализ), позволяющие подвести студентов к осознанию наиболее значимых способов получения и доказательства новых утверждений теории вероятностей с опорой на известные.
4. Завершающим элементом каждой цепочки являются рефлексивно-методические задачи. Они обеспечивают преобразование учебной деятельности, связанной с оперированием основными приемами мыслительной деятельности, в деятельность профессиональную, связанную с сознательным их использованием в качестве методов обучения и развития.
Приведем фрагмент цепочки задач для проведения практического занятия по теме «Геометрические вероятности».
Задача 1 (на синтез). Точка наудачу выбирается в круге радиуса R. Найти вероятность того, что она попадет внутрь данного вписанного квадрата.
Основу мыслительной деятельности студентов составляет прием синтеза. Условие задачи позволяет дать характеристику опыта – выбор точки в круге радиуса R. Опираясь на тот факт, что этот опыт имеет бесконечное число равновозможных исходов, студенты делают вывод о применимости геометрического способа определения вероятности и находят отношение площади вписанного квадрата в круг радиуса R к площади круга.
Задача 2 (на синтез). Точка случайным образом выбирается внутри каждого из квадратов (рис. 1). Внутри квадратов выделены кривые линии. Какой вывод можно сделать о вероятностях попадания точек на эти кривые?
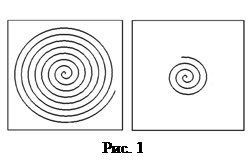
Изображенные кривые, как и в предыдущей задаче, провоцируют студентов на ложный вывод о том, что вероятность попадания точки на кривую в квадрате ![]() больше, чем на кривую в квадрате
больше, чем на кривую в квадрате ![]() . Однако проверка этого результата с помощью геометрического способа определения вероятности обнаруживает тот факт, что вероятности попадания равны, и равны нулю, так как данные кривые имеют площадь, равную нулю. В основе решения этой задачи также лежит прием – синтез.
. Однако проверка этого результата с помощью геометрического способа определения вероятности обнаруживает тот факт, что вероятности попадания равны, и равны нулю, так как данные кривые имеют площадь, равную нулю. В основе решения этой задачи также лежит прием – синтез.
При обсуждении этой задачи необходимо обратить внимание на следующий факт: из того, что вероятность события равна нулю, теоретически не следует, что событие невозможное.
Задача 3 (на анализ). Можно ли подтвердить вывод, сделанный в задаче 2, экспериментально.
В основе решения этой задачи лежит аналитическая деятельность. Для того чтобы сделать вывод о возможности экспериментального вычисления вероятности, необходимо знать, можно ли провести данный опыт довольно большое число раз, чтобы затем вычислить относительную частоту рассматриваемых в задаче событий. Ответ на вопрос задачи будет положительный, так как такая возможность имеется (например, с помощью моделирования случайных точек).
Задача 4 (на анализ). Можно ли вычислить вероятность перечисленных ниже событий как геометрическую вероятность?
a) Точка, наудачу поставленная на отрезке длиной 10 см, попадет на отрезок длины 5 см, расположенный внутри данного отрезка.
Пассажиру придется ждать электропоезда более 20 секунд, если поезда метро идут в данном направлении с интервалом 1 мин.
b) Наудачу выбранная точка в первой четверти координатной плоскости попадет в квадрат с вершинами (2; 2), (2; 4) (3; 4), (3; 2).
c) Попадание в определенную область мишени при условии, что выстрел сделан из ружья, у которого сбито прицельное устройство.
Данную задачу мы относим к задаче на анализ, т.к. суть ее решения составляет восстановление посылок, позволяющих сделать вывод о возможности применения геометрического способа определения вероятности. Ими будут: элементарное событие в опыте можно свести к выбору точки; элементарные события равновозможны; число элементарных событий бесконечно; а их множество образует конечномерную область (длину, площадь, объем). Решение данной задачи, по сравнению с предыдущими, связано с необходимостью интерпретации опыта как выбора точки в некоторой области. В случае а) опыт уже сформулирован как выбор точки на отрезке длиной 10 см. В случае b) опыт «приход пассажира к поезду в интервале между поездами» можно интерпретировать как случайный выбор точки (момента времени прихода пассажира к поезду) из временного интервала в 1 мин. Равновозможность элементарных событий следует из того, что нет никаких оснований считать, что один момент времени прихода пассажира более вероятен, чем другой. В случаях с) и d) опыты сформулированы в терминах выбора точки, однако геометрический способ в обоих случаях не применим: в случае с) в силу неизмеримости пространства элементарных исходов, в случае d) в силу неравновозможности исходов.
Задача 5 (на синтез через анализ). Расстояние от пункта А до пункта В автобус проходит за 2 мин., а пешеход – за 15 мин. Интервал движения автобусов 25 мин. Вы подходите в случайный момент времени к пункту А и отправляетесь в В пешком. Найдите вероятность того, что в пути вас догонит очередной автобус.

Решение задачи начинается с выбора способа определения вероятности (классического или геометрического), а именно восстановления условий применимости этих способов (прием анализа). На этом этапе цепочки анализ уже прост. Для этого формулируется опыт: «человек выходит из пункта А в случайный момент времени в течение (интервал движения автобуса)». Далее проверяются выделенные условия применимости геометрического способа определения вероятности (синтез). И, наконец, вычисляется вероятность как отношение длин отрезков (рис. 2) (синтез).
Задача 6 (на анализ через синтез). Стержень длины a наудачу ломают на 3 части. Найти вероятность, что длина каждой части окажется больше ![]() .
.
Данная задача относится уже к задачам на анализ через синтез. Прием позволяет сформулировать опыт на основе данных задачи и интерпретировать его в терминах выбора точки: опыт - «на отрезке длины а наудачу выбирают две точки». Его формулировка позволяет получить некоторые признаки применимости понятия геометрической вероятности: число элементарных событий бесконечно и даже несчетно, они в силу слова «наудачу» равновозможны. Для применимости понятия геометрической вероятности необходимо восстановить посылки (прием анализа), из которых может следовать конечномерность пространства элементарных событий. Для этого элементарное событие необходимо свести к выбору одной точки. Опыт работы показывает, что обнаружение необходимой интерпретации является сложной задачей для студентов, так как она требует отказа от отождествления понятия точки с привычным ее геометрическим образом. Преодолению этих затруднений помогает беседа с преподавателем, актуализирующая знания студентов о других образах точки (например, алгебраического).

Результатом поиска студентов, направляемого преподавателем, может стать, например, следующая интерпретация. Обозначим левую точку излома за x, а правую за y. Тогда элементарным событием является выбор точки (х;у) из треугольника: 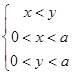 (рис. 3).
(рис. 3).
Найденная интерпретация доказывает конечномерность пространства элементарных исходов, а, следовательно, и применимость геометрического способа вычисления вероятности.
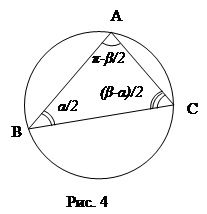
Задача 7 (на стратегию). На окружность радиуса R наудачу поставлены три точки А, В, С. Найдите вероятность того, что треугольник АВС остроугольный.
![]()
Так как число исходов опыта, описанного условием задачи, бесконечно, то для вычисления вероятности нужно воспользоваться геометрическим способом. Для этого опыт необходимо свести к выбору одной точки, задаваемой тремя координатами (x,y,z), значения которых определяются положением точек А, В и С соответственно на окружности. Но тогда пространство элементарных событий ![]() будет представлять собой трехмерную область, и построение множества точек, удовлетворяющих рассматриваемым событиям, становится затруднительным.
будет представлять собой трехмерную область, и построение множества точек, удовлетворяющих рассматриваемым событиям, становится затруднительным.
Для снятия этого затруднения временно упростим задачу. Для этого допустим, что положение одной из точек (пусть С) фиксированное. Если положение С фиксированное,
то положения А и В можно задавать величинами дуг СА=a, СВ=b, отсчитываемых против часовой стрелки (рис. 4).
Будем измерять дуги в радианах, тогда пара (a, b) – это точка в квадрате: <a<2p, 0<b<2p. Таким образом, задача сводится к вычислению отношения площадей (треугольника и квадрата).
Для распространения полученного результата на исходную задачу достаточно заметить, что при любом повороте окружности вероятность события и условие «остроугольности» сохраняются (свойство «вероятностной симметрии»).
Решение задачи основано на использовании стратегии «анализ в форме расчленения». Применение данной стратегии позволяет подвести студентов к осознанию способов переноса результатов решения простейших задач теории вероятностей на более сложные (в данном случае таким способом является использование свойства «вероятностной симметрии»).
Идея решения приведенной выше задачи является достаточно нестандартной. При этом преподаватель должен выступить не с идеей варианта решения, а с вопросом или серией вопросов, провоцирующих появление данной идеи. Деятельность преподавателя здесь должна быть направлена на развитие воображения или интуиции студента. Не исключается и возможность предложить эту задачу студентам для самостоятельного решения.
Задача 8 (анализ через синтез). Можно ли при решении приведенных ниже двух задач воспользоваться свойством симметрии, т.е. зафиксировать одну точку, а две другие считать случайными относительно нее?
8.1. На окружности наудачу брошены три точки. Найдите вероятность того, что они образуют вершины: а) какого-нибудь треугольника; б) правильного треугольника; в) прямоугольного треугольника.
8.2. На отрезок наудачу бросают три точки, одну за другой. Какова вероятность того, что третья по счету точка упадет между двумя первыми?
Для ответа на вопрос необходимо восстановить условия применимости свойства симметрии, принятого в теории вероятностей (прием анализа), и затем рассмотреть их применительно к сформулированным опытам.
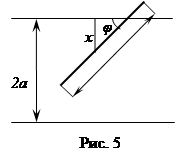
Задача 9 (на стратегию). (Задача Бюффона об игле, 1777 г.). Плоскость разграфлена параллельными прямыми, расстояние между которыми равно 2а.
На эту плоскость наудачу брошена игла длиной 2l (l![]() a). Найдите вероятность того, что игла пересечет какую-нибудь прямую.
a). Найдите вероятность того, что игла пересечет какую-нибудь прямую.
Первой идеей (аналитическая деятельность) при решении является то, что достаточно рассматривать одну полосу, так как при попадании иглы в другую полосу вероятность события будет сохраняться (свойство симметрии). Затем при определении элементарного события в данном опыте необходимо выделить совокупность величин, полностью определяющих положение иглы (также аналитическая деятельность). За элементарное событие можно принять точку (x, y), где x – расстояние от центра иглы до ближайшей параллели, y – радианная мера угла, составленного иглой с этой параллелью (рис. 5).
Далее требуется синтетическая деятельность. Всевозможные положения иглы определяются точками прямоугольника со сторонами a и ![]() . Для пересечения иглы с параллелью необходимо и достаточно, чтобы
. Для пересечения иглы с параллелью необходимо и достаточно, чтобы ![]() . Искомая вероятность в силу сделанных предположений равна:
. Искомая вероятность в силу сделанных предположений равна: 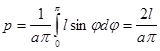
![]() .
.
Задача 10 (рефлексивно-методическая). Сколько раз использовался прием «вероятностной симметрии» при решении задачи 9? Можно ли еще раз применить данное свойство при решении задачи?
В указанном плане решения мы обратили внимание на применение этого приема только один раз. На самом же деле несознательно его мы использовали и дальше. Для ответа на этот вопрос студентам придется проанализировать весь ход решения задачи 9.
Рецензенты:
Шабанова М.В., д.п.н., профессор, профессор кафедры методики преподавания математики, Института математики, информационных и космических технологий ФГАОУ ВПО «Северный (Арктический) федеральный университет имени М.В. Ломоносова», г. Архангельск.
Санина Е.И., д.п.н., профессор, профессор кафедры высшей математики ФГБОУ ВПО «Российского университета дружбы народов», г. Москва.



