Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Умение культивировать долгосрочные отношения со стейкхолдерами (обществом, государством, персоналом, клиентами, бизнесом и др.) есть фактор устойчивых конкурентных преимуществ современного вуза, позволяющий ему присваивать отношенческие ренты [6, 7]. Установление и поддержание сбалансированных отношений с заинтересованными сторонами требует способности объективно оценить сложившиеся отношения и возможности их изменений.

Стратегии взаимодействия организации с каждой группой заинтересованных сторон (ГЗС) лежат в основе стратегий всех уровней (корпоративной стратегии, бизнес-стратегий, функциональных и операционных стратегий). Выбор набора стратегий взаимодействия с ГЗС обуславливается стремлением организации к долгосрочной сбалансированности отношений со всеми ее стейкхолдерами. Выбор того или иного типа стратегии взаимодействия организации с конкретной ГЗС определяется, с одной стороны, результатами оценки организацией сложившихся отношений и возможностей их изменений [8, 9], с другой стороны, степенью развитости соответствующих компетенций организации (наличием ключевых компетенций), необходимых для реализации каждого из возможных типов стратегий [5].

В работах [7–9] был предложен методический подход к выбору типа стратегии взаимодействия вуза с каждой его заинтересованной стороной (удовлетворение запросов, защита, воздействие или сотрудничество).

В свою очередь, в работах [1–3] описана методика сценарного анализа отношений вуза с его группами заинтересованных сторон с учетом отношений ГЗС между собой. На четвертом этапе данной методики производился расчет и анализ весовых коэффициентов целесообразности применения типов стратегий взаимодействия вуза с ГЗС. При этом при принятии решения о выборе типа стратегии взаимодействия для каждой ГЗС учитывалась «устойчивость» соответствующего коэффициента относительно различных сценариев. Для оценки устойчивости данные коэффициенты для разных сценариев рассматривались как дискретные случайные величины, для которых рассчитывались и принимались во внимание по отдельности математическое ожидание () и дисперсия (). Однако выбор стратегии на основе данных критериев по отдельности зачастую оказывается противоречивым. Остается нерешенной проблема окончательного выбора оптимальной стратегии на основе критерия, который соединял бы в себе и .

Рассмотрим следующий пример. В таблице 1 представлены весовые коэффициенты целесообразности применения типов стратегий взаимодействия вуза с клиентами.

Таблица 1. Весовые коэффициенты целесообразности применения типов стратегий взаимодействия

Как видно из таблицы, представленные случайные величины – весовые коэффициенты целесообразности применения типов стратегий относительно различных сценариев ( – количество типов стратегий, – количество принимаемых во внимание сценариев) – характеризуются парой показателей: математическим ожиданием и среднеквадратичным отклонением (для каждого конкретного типа стратегий).

Для того чтобы выбрать наиболее подходящий тип стратегии взаимодействия, рассмотрим задачу двухкритериальной оптимизации, где в качестве частных критериев выступают и . В работе [4] для решения данной задачи предлагается использовать обобщенный критерий, который представляет собой взвешенную сумму частных критериев и с весовыми коэффициентами 1 и :

где – некоторая постоянная.

Значение характеризует склонность к риску лица, принимающего решение (ЛПР). При >0 ЛПР не склонно к риску, так как в этом случае оценка случайной величины, полученная с помощью обобщенного критерия, меньше чем ее среднее значение, что характеризует осторожного человека. При <0 складывается обратная ситуация, ЛПР склонно к риску. Наконец, при =0 ЛПР безразлично к риску, так как оценка (1) случайной величины совпадает с ее средним значением.

Представим рассматриваемые типы стратегий взаимодействия точками на координатной плоскости переменных (рисунок 1). На рисунке можно легко определить Парето-оптимальное множество типов стратегий (удовлетворение запросов (У), защита (З), сотрудничество (С)).

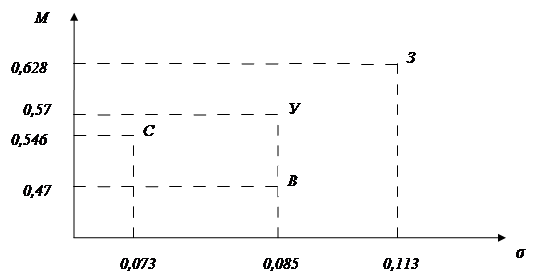
Рисунок 1. Соотношение математического ожидания и среднеквадратичного отклонения для типов стратегий взаимодействия

Окончательный выбор оптимального типа стратегии должен производиться из этого множества. Стратегию воздействия (В) можно исключить из дальнейшего рассмотрения, так как остальные стратегии превосходят данную стратегию по Парето. Стратегии (С), (У), (З) несравнимы по Парето. Сужение Парето-оптимального множества может быть произведено только при наличии дополнительной информации о соотношении критериев и .

Найдем оптимальную стратегию с помощью обобщенного критерия . Здесь . Для установления ранжирования Парето-оптимального множества (С, У, З) по обобщенному критерию , найдем нижнюю границу меры несклонности к риску и верхнюю границу меры несклонности к риску по следующим формулам [4]:

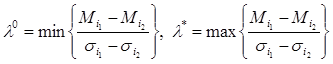
где и – математическое ожидание и среднеквадратичное отклонение двух фиксированных альтернатив и ; операторы min и max распространяются на такие пары индексов (), для которых альтернативы оптимальны по Парето. Причем и .

Получим:, , .

Отсюда: .

Таким образом, интервал (0, +) можно разбить на три интервала: (0; 2) – зона малой несклонности к риску (зона малой осторожности); (2; 2,071) – зона неопределенности; (2,071; +) – зона большой несклонности к риску (зона большой осторожности) (рисунок 2).

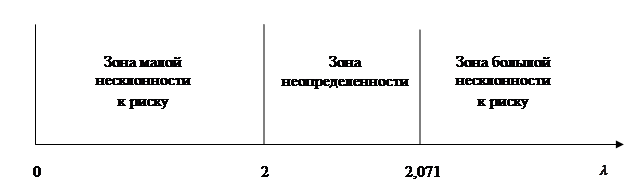
Рисунок 2. Зоны несклонности к риску

Если для ЛПР его мера несклонности к риску , то для него ранжирование множества Парето-оптимальных альтернатив совпадает с их ранжированием по величине ожидаемого выигрыша: (знаком обозначается предпочтение по величине обобщенного критерия ). При этом оптимальной будет стратегия защиты (З).

Если для ЛПР его мера несклонности к риску , то для него ранжирование множества Парето-оптимальных альтернатив совпадает с их ранжированием по показателю риска: . При этом оптимальной будет стратегия сотрудничества (С).

Рассмотрим случай, когда мера несклонности к риску ЛПР попадает в зону неопределенности. Возьмем, например, . Тогда ; ; . Получаем ранжирование . Таким образом, в этом случае предпочтение для пары (У, З) определяется по величине ожидаемого выигрыша, а для пары (С, З) – по величине риска.

Таким образом, проблема выбора типа стратегии взаимодействия вуза со стейкхолдерами в условиях риска может быть решена с использованием обобщенного критерия . Однако в таком случае возникает вопрос определения для ЛПР его несклонности (или склонности) к риску. Здесь можно отметить, что данный параметр является субъективно-психологическим качеством человека и определяется из наблюдений за тем, как ЛПР принимает решения в рисковых ситуациях.

Описанный выше метод выбора альтернатив является не единственным и имеет ряд недостатков, наиболее существенный из которых состоит в том, что критерий основывается на предположении постоянства меры несклонности к риску ЛПР. Вместе с тем для большинства людей их мера склонности к риску меняется в зависимости от величины ожидаемого выигрыша и степени риска. Также недостатком метода является необходимость в большой дополнительной информации о соотношении математического ожидания и среднеквадратичного отклонения. Однако при выборе типов стратегий взаимодействия вуза со стейкхолдерами этот недостаток отсутствует, так как математические ожидания и среднеквадратичные отклонения можно точно рассчитать. Преимуществом же метода является то, что для установления ранжирования альтернатив достаточно знать не точное значение показателя , а некоторый интервал, в который он входит.

Рецензенты:

Ембулаев Владимир Николаевич, д-р экон. наук, д-р транспорта, доцент, ФГБОУ «Владивостокский государственный университет экономики и сервиса», г. Владивосток.

Мазелис Лев Соломонович, д-р экон. наук, директор института информатики, инноваций и бизнес-систем, заведующий кафедрой математики и моделирования, ФГБОУ «Владивостокский государственный университет экономики и сервиса», г. Владивосток.