С развитием сети Интернет правительства многих стран мира ощущают положительное влияние высокоскоростных сетей на коммерческие компании, общественные организации и рядовых граждан. Широкополосные сети давно стали неотъемлемой частью инфраструктуры мирового информационного сообщества. Они предоставляют пользователям постоянный высокоскоростной доступ к разнообразным веб-сервисам, контенту и программному обеспечению.
Недавние исследования доказали, что наличие надежных широкополосных сетей стимулирует рост ВВП промышленно развитых стран и может обеспечить аналогичные преимущества для стран с развивающейся рыночной экономикой. Поэтому возникает проблема надёжности программного обеспечения (ПО) технологии доступа к широкополосным мультимедийным услугам.
Предлагаются модели оценки надежности модульных структур N-вариантных программных систем, позволяющие алгоритмизировать оптимизационные процедуры, учитывающие фактор N-вариантности критического по отказоустойчивости ПО. Рассматриваются четыре типа базовых моделей оптимизации надежности программных систем (включая N-вариантные структуры) при ограничениях на использование доступных стоимостных ресурсов.
Предлагаемая концепция СОТS-сопровождения N-вариантного программирования обеспечивает доступность математических моделей для оценки надежности версий модулей, что позволяет иметь информацию относительно как надежности ПО, так и его стоимости. Кроме того, следует отметить, что одно из главных преимуществ N-вариантного ПО – это независимость отказа избыточных версий модулей.
На основе концепции СОТS-сопровождения N-вариантного программирования предлагается модель этапа постархитектуры для оценки стоимости N-вариантного ПО, которая используется в период, когда уже сформирована архитектура системы и выполняется дальнейшая разработка N-вариантных структур программного продукта. Основное уравнение постархитектурной модели является развитием уравнения модели СОСОМО II и имеет следующий вид:
![]()
где: коэффициент Кreq учитывает изменения в требованиях при формировании V-спецификаций на N-вариантные компоненты ПО;
показатель В отражает нелинейную зависимость затрат от размера проекта (размер выражается в KLOC), вычисляется так же, как и в предыдущих моделях COCOMO;
в размере проекта различают две составляющие – новый код и N-вариантный (повторно и многократно используемый код);
множитель поправки Мp зависит от 17 факторов затрат, характеризующих продукт, аппаратуру, персонал и проект.
Изменчивость требований при формировании N-вариантных компонент программных систем приводит к повторной работе, требуемой для учета предлагаемых изменений. Оценка их влияния выполняется по формуле
Кreq = l + (BRAK /100),
где BRAK – процент кода, отброшенного (модифицированного) из-за изменения требований.
Размер проекта и продукта определяют по выражению
SIZE = SIZEnew + SIZEreuse [KLOC],
где:
SIZEnew – размер нового (создаваемого) программного кода;
SIZEreuse – размер повторно используемого программного кода N-вариантных компонент ПО.
Формула для расчета размера повторно используемого кода записывается следующим образом:
![]()
где
KASLOC – количество строк повторно используемого кода, который должен быть модифицирован (в тысячах строк);
AT – процент автоматически генерируемого кода;
DM – процент модифицируемых проектных моделей;
СМ – процент модифицируемого программного кода;
IM – процент затрат на интеграцию N-вариантных структур ПО, требуемых для подключения многократно/повторно используемого ПО;
SU – фактор, основанный на стоимости понимания добавляемого ПО, изменяется от 50 (для сложного неструктурированного кода) до 10 (для хорошо написанного объектно-ориентированного кода).
Фактор АА отражает стоимость решения о том, может ли он быть повторно используемым в N-вариантных программных структурах мультиверсионной системы. Он зависит от размера требуемого тестирования и поддержки n-вариантного исполнения (величина изменяется от 0 до 8).
Для определения множителя поправки Мр основного уравнения используют 17 факторов затрат, которые могут быть разбиты на 4 категории: факторы продукта; факторы платформы исполнения (виртуальной машины); факторы персонала; факторы проекта. Для каждого фактора определяется оценка (по 6-балльной шкале). На основе оценки для каждого фактора по таблице Боэма определяется множитель затрат ЕМj (j=1,…,17). Перемножение всех множителей затрат дает множитель поправки постархитектурной модели.
Значение Мр отражает реальные условия выполнения программного проекта и позволяет троекратно увеличить (уменьшить) начальную оценку затрат. От оценки затрат легко перейти к стоимости проекта, а после определения затрат и стоимости можно оценить длительность разработки N-вариантной структуры. Модель СОСОМО II содержит уравнение для оценки календарного времени TDEV, требуемого для выполнения проекта. Для моделей всех уровней справедливо:
![]()
где:
В – ранее рассчитанный показатель степени,
SCEDpercentage – процент увеличения (уменьшения) номинального графика.
Далее в работе рассматривается четыре модели, каждая из которых применима к различным структурам N-вариантных (или мультиверсионных) систем (от очень простой структуры к более сложной). Многообразие моделей дает проектировщику гибкость в выборе соответствующей модели для проектируемой системы. Рассматривается структура моделей и представлена постановка задачи и методы решения для каждой из них с учетом следующих условных обозначений:
K – число функций N-вариантной программной системы, которые необходимо выполнить;
n – число модулей N-вариантной программной системы;
Fk – частота использования k-й функции ПО, k = 1,2,...,K;
mi – число версий, i-го модуля, i = 1, ...,n;
Rij – оценка надежности j-й версии i-го модуля;
Xij – булева переменная, равная 1, если j-я версия выбрана для i-го модуля, иначе - 0;
Ri – оценка надежности i-го модуля;
R – оценка надежности N-вариантной программной системы;
Сij – стоимость разработки и сопровождения j-й версии i-го модуля;
B – ограничение по стоимости создаваемой N-вариантной программной системы.
Как и ранее, имеют силу основные предположения методологии N-вариантного проектирования ПО, касающиеся, во-первых, использования методов модульного программирования; во-вторых, независимости разработки версий модулей и осуществимости оценки их надежности и стоимости с использованием модулей COTS-сопровождения (эти модули производятся и тестируются независимо, поэтому их надежность может быть оценена с помощью любой из доступных моделей, а их фактическая стоимость – это стоимость закупки и сопровождения); в-третьих, имеется ограничение на стоимость N-вариантной программной системы (N-ВПС).
Обобщающей моделью является модель В-2, формирующая оптимальный состав модулей многофункциональной (К-функций) N-вариантной программной системы с введением избыточности. Ввиду того, что избыточность в структуре разрешена, возможен выбор более чем одной версии для каждого модуля программной системы. Задача сформулирована следующим образом:
![]()
при ограничениях:
![]()
![]()
Xij = 0,1 j = 1,…,mi, i = 1,…,n,
![]()
Надежность i-го модуля определяется как вероятность того, что, по крайней мере, одна из тi версий выполняется правильно, а совокупность ограничений гарантирует, что для каждого i-го модуля выбрана, по крайней мере, одна версия.
Из-за наличия ограничений и так как мы имеем дело с функциями системы ПО, ни один из методов, предложенных ранее, не может быть «напрямую» использован для решения задачи В-2. Кроме того, целевая функция – нелинейная, поэтому в работе предложен метод линеаризации и представлены численные примеры решения задачи оптимизации состава версий модульных N-вариантных программных структур.
Решение задачи формирования мультиверсионного ПО принадлежит множеству, определяемому следующим выражением
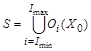 (1)
(1)
где X0 – точка пространства булевых переменных, все координаты которой имеют нулевое значение.
Таким образом, чтобы найти решение задачи, достаточно сравнить значения целевой функции в элементах множества S. Данное свойство позволяет значительно уменьшить вычислительные затраты на поиск точного решения, ускоряя тем самым выполнение процедуры поиска. Мощность множества S определяется следующим выражением
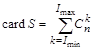
где ![]() – число сочетаний из n элементов по k.
– число сочетаний из n элементов по k.
Схема поиска на множестве решений, определяемом выражением (1), была реализована и опробована в алгоритме Truncation Exhaustive Search (усеченный полный перебор).
Ограничение на стоимость проектируемого комплекса программ имеет вид
![]()
где 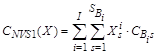 (2)
(2)
Ограничение на стоимость проектируемого комплекса программ определяется выражением
![]()
где 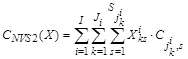 (3)
(3)
Для приведенных выше псевдобулевых функций (2), (3) выделяется следующее свойство: если две соседние друг к другу точки X и Y отличаются значением некоторой i-ой компоненты, причем Xi=0, а Yi=1, то C(Y)=C(X)+Ci, где Ci – стоимость включения в структуру мультиверсии, соответствующей i-й компоненте вектора участия. Полностью значение функции-ограничения для каждой из моделей вычисляется в некоторой начальной точке поиска. Все же последующие значения этой функции получаются прибавлением либо вычитанием соответствующей величины при переходе по соседним точкам.
С целью утилизации вышеописанного свойства построенной оптимизационной задачи была реализована процедура обхода графа булевых переменных по соседним точкам, причем каждая точка области решений просматривается алгоритмом обхода только один раз, что позволяет избежать повышения вычислительной сложности поисковых процедур. Такой способ обхода области поиска был реализован в алгоритме неявного перебора с обходом области поиска по соседним точкам [5]. Поиск осуществляется по направлению от точки X0={0,…,0} к точке X1={1,…,1} – координаты принимают единичные значения. На практике реализация обратно направленного обхода (для этого в блок-схеме нули заменяются единицами, а единицы – нулями) может оказаться более эффективной.
Так, метод изменяющихся вероятностей (МИВЕР) представляет семейство алгоритмов, имеющих общую схему [3]. В применении к задаче формирования мультиверсионного ПО из разработанных ранее алгоритмов схемы МИВЕРа на основе экспериментальных данных наиболее эффективным был признан модифицированный алгоритм случайного поиска с возвратом (МСПА) с независимым распределением вероятностей.
Выше было показано, что вид целевых функций в построенных оптимизационных задачах обуславливает наличие множества постоянства, на котором целевая функция приобретает нулевое значение. Как показала практика, на каждом этапе поиска с использованием алгоритмов СПА (случайный поиск с адаптацией) и МСПА возможна генерация большого числа подобных «нулевых» точек. Поэтому во избежание генерации точек, придающих нулевое значение целевой функции, были разработаны алгоритмы NVS СПА и NVS МСПА, отличающиеся от своих аналогов правилами формирования компонент вектора вероятностей и генерации случайных точек.
Вектор вероятностей «разбивается» на I частей, каждая из которых содержит Li, i=![]() компонент в соответствии с числом программных модулей в формируемом комплексе. Значения компонент вектора вероятностей P определяются таким образом, чтобы сумма значений компонент, соответствующих одному программному модулю, была равна единице, то есть
компонент в соответствии с числом программных модулей в формируемом комплексе. Значения компонент вектора вероятностей P определяются таким образом, чтобы сумма значений компонент, соответствующих одному программному модулю, была равна единице, то есть
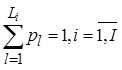
При реализации первой оптимизационной модели формирования мультиверсионного программного обеспечения значения параметров Li определяются как
![]()
а для второй модели
![]()
На первом этапе алгоритмов компоненты исходного вектора вероятностей P0 полагаются равными ![]() , что определяет частично независимое распределение вероятностей присвоения единичного значения каждой компоненте
, что определяет частично независимое распределение вероятностей присвоения единичного значения каждой компоненте ![]() . Случайный выбор конкретного вектора определяется n испытаниями, каждое из которых определяет значение соответствующей компоненты вектора булевых переменных: организуются I циклов испытаний по Li случайных выборов компонент булевого вектора, которым присваиваются единичные значения.
. Случайный выбор конкретного вектора определяется n испытаниями, каждое из которых определяет значение соответствующей компоненты вектора булевых переменных: организуются I циклов испытаний по Li случайных выборов компонент булевого вектора, которым присваиваются единичные значения.
При тестировании этого алгоритма была выявлена стабильность в нахождении решений. На практике эта особенность алгоритма случайного поиска граничных точек может позволить сократить число вычислений за счет уменьшения параметра L – числа итераций алгоритма.
Предложенные технические и технологические решения и созданные на их основе методы и средства позволяют создать и поддерживать эффективную по затратам времени и ресурсов, независимую от используемой целевой вычислительной платформы и гарантирующую требуемый уровень качества технологию проектирования, разработки и долговременного сопровождения ПО для надёжного доступа к широкополосным мультимедийным услугам.
Исследование выполнено при поддержке Министерства образования и науки Российской Федерации, соглашение 14.B37.21.0625.
Рецензенты:
Петров Михаил Николаевич, д.т.н., профессор, зав. кафедрой электронной техники и телекоммуникаций Сибирского государственного аэрокосмического университета, г.Красноярск.
Пимонов Александр Григорьевич, д.т.н., профессор, профессор кафедры прикладных информационных технологий ФГБОУ ВПО «Кузбасский государственный технический университет имени Т. Ф. Горбачева», г. Кемерово.



