Введение
В процессе глобализации экономики и усложнения хозяйственных связей промышленные предприятия вынуждены искать новые способы повышения эффективности деятельности и реализации неиспользуемых в данный момент резервов для роста. Оценка и оптимизация происходящих на промышленном предприятии интеграционных и квазиинтеграционных процессов вызывает существенные сложности, в том числе и в области оптимизации процессов на стадиях кругооборота оборотных средств. Наиболее сложной задачей для решения данных вопросов является оценка и оптимизация уровня риска ввиду того, что в настоящий момент недостаточно разработан алгоритм определения оптимального риска в кругообороте оборотных средств промышленного предприятия [1; 2].
Рассмотрим более детально процесс выбора оптимальных решений с целью оптимизации уровня риска на долгосрочную и краткосрочную перспективы.
Блок-схема процесса выбора оптимального решения представлена на рисунке 1.
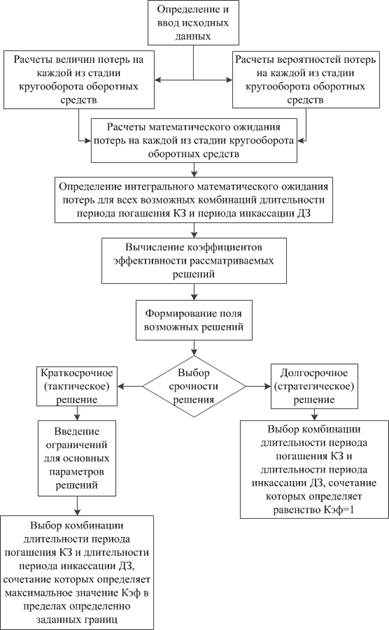
Рисунок 1. Блок-схема алгоритма оптимизации
На первом этапе необходимо определить и ввести исходные данные в экономико-математическую модель. На данном этапе фиксируются постоянные и переменные относительно длительности периода погашения кредиторской задолженности и длительности периода инкассации дебиторской задолженности величины. Эти данные могут быть получены исходя из имеющейся у предприятия статистической информации, а также определены экспертным путем с привлечением специалистов, работающих на анализируемом предприятии [3].
На втором этапе на основе разработанного в диссертационном исследовании метода оптимизации уровня риска по стадиям кругооборота оборотных средств необходимо произвести необходимые расчеты для формирования поля возможных решений: определить величины потерь и их вероятности на каждой из стадий кругооборота оборотных средств. Следующим шагом должно стать вычисление размеров математических ожиданий потерь на каждой из стадий, и в результате их суммирования необходимо определить интегральное математическое ожидание потерь [6].
Для улучшения наглядности и эффективности разработанного алгоритма рассмотрим его на примере промышленного предприятия ЗАО «Чистый Урал», занимающегося производством профессиональных моющих и дезинфицирующих средств. Предприятие осуществляет производственную деятельность более 10 лет. В течение этого времени им было осуществлено развитие из небольшого предприятия в одного из лидеров в области производства и поставок профессиональных моющих средств для мясоперерабатывающих предприятий Южно-Уральского региона.
Данный объект исследования выбран неслучайно: предприятие относится к кластеру химической промышленности, товарная номенклатура которого определяет санитарно-гигиеническую обстановку на предприятиях пищевой промышленности, медицины и бытового обслуживания в регионе. В связи с безусловной важностью этих отраслей для региона вопросы управления рисками по стадиям кругооборота оборотных средств на данном предприятии являются актуальными.
Отметим, что за 10-летнюю историю развития предприятия сформированы долгосрочные отношения с поставщиками материальных ресурсов и потребителями продукции, выражающиеся в виде долгосрочных контрактов и частичной информационной открытости. Исходя из этого, можно говорить о том, что исследуемое предприятие находится в стадии квазиинтеграции с поставщиками материальных ресурсов и потребителями готовой продукции. В нашем примере будем рассматривать направление производства жидкого мыла.
Итак, завершив второй этап, мы должны располагать некоторым распределением совокупного математического ожидания потерь на всех стадиях. В нашем случае такое распределение визуализировано в виде трехмерного графика, изображенного на рисунке 2.
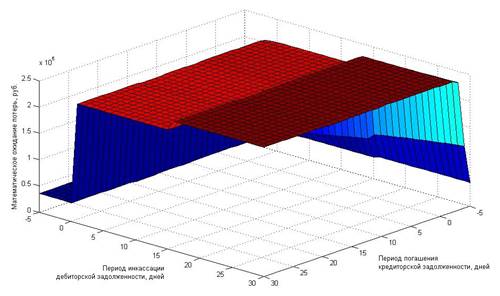
Рисунок 2. Совокупное математическое ожидание потерь на всех стадиях кругооборота оборотных средств
Исследуя данное распределение, мы можем сказать, что основная область наиболее эффективных решений для снижения величины ожидаемых потерь на всем поле возможных решений ограничена длительностью периода инкассации дебиторской задолженности от -5 до 1 дня вне зависимости от длительности периода погашения кредиторской задолженности. Наиболее высокие значения совокупного математического ожидания потерь можно наблюдать в области, ограниченной длительностью периода инкассации дебиторской задолженности от 16 до 30 дней вне зависимости от длительности периода погашения кредиторской задолженности.
Рассмотрим данную область эффективных решений более внимательно. При ближайшем рассмотрении мы видим, что на всей области возможных решений минимальное значение интегрального математического ожидания потерь, равное 34 134,20 руб., обеспечивает сочетание длительности периода погашения кредиторской задолженности 16-19 дней и длительности периода инкассации дебиторской задолженности, равная 0 дней.
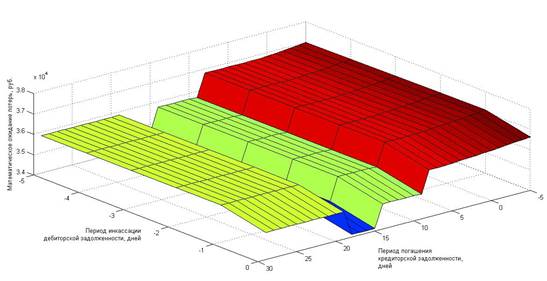
Рисунок 3. Совокупное математическое ожидание потерь на всех стадиях кругооборота оборотных средств на участке поиска решений
Результаты всех оставшихся комбинаций длительностей периода погашения кредиторской задолженности и периода инкассации дебиторской задолженности рассматриваются относительно определенного выше наилучшего решения, затем определяется коэффициент эффективности решения, определяемый по формуле 1.
![]() , (1)
, (1)
где Интегр. Rmin – минимальное значение интегрального математического ожидания потерь на всей области возможных решений; Интегр. Rij – значения интегрального математического ожидания потерь при i-длительности периода погашения кредиторской задолженности и j-длительности периода инкассации дебиторской задолженности.
В результате преобразований получаем трехмерный график, изображенный на рисунке 4, который позволяет визуализировать эффективность принимаемых решений относительно наилучшего. Отметим, что значение коэффициента эффективности наилучшего решения равен 1, так как ![]() . Таким образом, чем ближе коэффициент эффективности решения к 1, тем более предпочтительным оно является.
. Таким образом, чем ближе коэффициент эффективности решения к 1, тем более предпочтительным оно является.
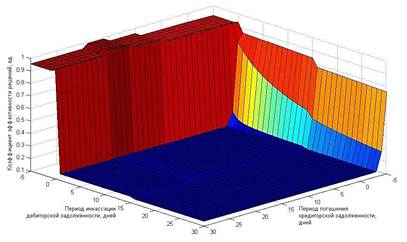
Рисунок 4. Поле возможных решений
Итак, определенные таким образом значения коэффициента эффективности решения для каждого из сочетаний периода погашения кредиторской задолженности и периода инкассации дебиторской задолженности формируют поле возможных решений [4].
Определим текущее значение интегрального математического ожидания потерь на всех стадиях кругооборота оборотных средств производителя, находящегося в условиях квазиинтеграции с поставщиком материальных ресурсов и покупателем готовой продукции, и оценим его эффективность относительного наилучшего решения, используя коэффициент эффективности, определяемый по формуле 1. Текущее значение предопределено сочетанием условий взаимодействий с квазиинтегрированными контрагентами: период погашения кредиторской задолженности перед поставщиком материальных ресурсов составляет 14 дней, длительность периода инкассации дебиторской задолженности составляет 21 день. При таком сочетании величина текущего интегрального математического ожидания потерь составляет 246 267,36 руб.
Теперь рассмотрим области долгосрочных и краткосрочных решений с целью оптимизации уровня риска. Очевидно, что область стратегических решений должна быть существенно шире, чем область тактических. При текущих условиях работы сложно и проблематично резко изменить длительности периода погашения кредиторской задолженности и длительности периода инкассации дебиторской задолженности [5].
Отметим, что найденное выше оптимальное решение в виде сочетания длительности периода погашения кредиторской задолженности 16-19 дней и длительности периода инкассации дебиторской задолженности 0 дней, дающее величину интегрального математического ожидания потерь 34 134,20 руб. является скорее стратегическим решением, определяющим вектор принятия решений в долгосрочном периоде. Это обусловлено тем, что при текущих условиях работы с квазиинтегрированными контрагентами в действительности будет сложно изменить длительность периода погашения кредиторской задолженности и длительность периода инкассации дебиторской задолженности.
В первом случае такая сложность связана прежде всего с тем, что поставщик материальных ресурсов в краткосрочном периоде не всегда согласится пойти на условия увеличения периода погашения кредиторской задолженности, при этом в долгосрочном периоде – скорее всего такое изменение может быть принято.
В ситуации с изменением длительности периода инкассации дебиторской задолженности может возникнуть проблема в области его уменьшения, так как существует активно конкурентная среда, которая формирует альтернативные предложения и условия работы и предлагает их покупателю готовой продукции. К числу этих условий относится и длительность периода инкассации дебиторской задолженности.
В связи с этим для достижения краткосрочных целей оптимизации уровня риска производителя, находящегося в стадии квазиинтеграции с поставщиком материальных ресурсов и покупателем готовой продукции, определим следующие границы выбора решения: длительность периода погашения кредиторской задолженности – от -5 до 20 дней; длительность периода инкассации дебиторской задолженности от 10 до 30 дней.
Для визуализации поля решений построим трехмерные графики в пределах заданных выше границ, отражающие величину интегрального математического ожидания потерь и коэффициента эффективности решений. Результаты построения представлены на рисунках 5 и 6.
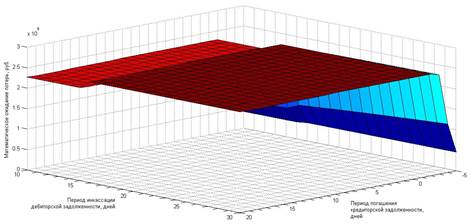
Рисунок 5. Интегральное математическое ожидание в пределах заданных границ

Рисунок 6. Коэффициенты эффективности решений в пределах заданных границ
На графике, изображенном на рисунке 6, отчетливо видна область наиболее эффективных решений для краткосрочного периода, ограниченная длительностью периода погашения кредиторской задолженности от -5 до -3 дней и длительностью периода инкассации дебиторской задолженности от 10 до 15 дней. Осуществим выборку значений составляющих интегрального математического ожидания потерь для данных вариантов и рассмотрим их в виде таблицы 1.
Таблица 1
|
Дл-сть периода погашения КЗ, дней |
Дл-сть периода инкассации ДЗ, дней |
Математическое ожидание потерь на стадиях кругооборота ОС, руб. |
Интегральное мат. ожидание, руб. |
Кэф |
||||||||
|
Поставщик матер. ресурсов |
Снабжение |
Складирование, хранение и внутр. транс-ка ресурсов |
Производство |
Складирование, хранение и внутр. транс-ка ГП |
Сбыт. Продажи. Маркетинг. |
Транспортиров-ка ГП |
Финансирование |
Покупатель ГП |
||||
|
-5 |
10 |
12760,24 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
6597,71 |
35,42 |
40517,04 |
0,842 |
|
-5 |
11 |
12784,00 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
6655,21 |
35,42 |
40598,30 |
0,841 |
|
-5 |
12 |
12807,76 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
6712,67 |
35,42 |
40679,52 |
0,839 |
|
-5 |
13 |
12831,52 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
6770,10 |
35,42 |
40760,71 |
0,837 |
|
-5 |
14 |
12855,28 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
6827,49 |
35,42 |
40841,87 |
0,836 |
|
-5 |
15 |
12879,04 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
6884,86 |
35,42 |
40922,99 |
0,834 |
|
-4 |
10 |
12736,48 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
34444,53 |
35,42 |
68340,11 |
0,499 |
|
-4 |
11 |
12760,24 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
36823,91 |
35,42 |
70743,24 |
0,483 |
|
-4 |
12 |
12784,00 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
39133,68 |
35,42 |
73076,77 |
0,467 |
|
-4 |
13 |
12807,76 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
41376,86 |
35,42 |
75343,71 |
0,453 |
|
-4 |
14 |
12831,52 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
43556,29 |
35,42 |
77546,90 |
0,440 |
|
-4 |
15 |
12855,28 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
45674,65 |
35,42 |
79689,02 |
0,428 |
|
-3 |
10 |
12712,72 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
177932,03 |
35,42 |
211803,84 |
0,161 |
|
-3 |
11 |
12736,48 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
179330,53 |
35,42 |
213226,10 |
0,160 |
|
-3 |
12 |
12760,24 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
180513,44 |
35,42 |
214432,77 |
0,159 |
|
-3 |
13 |
12784,00 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
181527,05 |
35,42 |
215470,15 |
0,158 |
|
-3 |
14 |
12807,76 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
182405,28 |
35,42 |
216372,13 |
0,158 |
|
-3 |
15 |
12831,52 |
2247,78 |
71,44 |
4348,31 |
105,78 |
15349,12 |
-998,76 |
183173,55 |
35,42 |
217164,16 |
0,157 |
Выборка значений составляющих математического ожидания потерь
Таким образом, мы видим, что для краткосрочного периода наилучшим решением по оптимизации уровня риска является длительность периода погашения кредиторской задолженности, равная -5 дням, и периода инкассации дебиторской задолженности, равная 10 дням. При таких условиях взаимодействия в условиях квазиинтеграции с поставщиком материальных ресурсов и покупателем готовой продукции производитель достигнет снижения значения математического ожидания потерь до 40 517,04 руб., что снизит этот показатель на 83,55% относительно текущего. При этом данные значения могут быть реально достигнуты в краткосрочном периоде, так как решение было выбрано с учетом определенных для этого границ [3].
Напомним, что в долгосрочной перспективе наилучшим решением является сочетание длительности периода погашения кредиторской задолженности, равной 16-19 дням, и длительности периода инкассации дебиторской задолженности, равной -5 дням. При достижении таких условий величина интегрального математического ожидания потерь снизится с 246 267,36 руб. (текущее значение) до 34 134,20 руб., что составляет снижение на 86,14%.
В результате мы можем сделать вывод о высокой эффективности используемого алгоритма определения оптимального риска в кругообороте оборотных средств промышленного предприятия, находящегося в условиях квазиинтеграции с поставщиком материальных ресурсов и покупателем готовой продукции.
Данная статья подготовлена в рамках Госзадания Минобрнауки РФ «Организационно-экономическое обеспечение инновационного управления предприятием» 2012-2014 гг.
Рецензент:
Баев Игорь Александрович, доктор экономических наук, декан факультета экономики и управления ФГБОУ ВПО «ЮУрГУ» (НИУ), г. Челябинск.



