УДК 681.3:621.396:536.2
ОЦЕНКА АДЕКВАТНОСТИ МОДЕЛИ ДЛЯ РАСЧЕТА ТЕМПЕРАТУРНОГО ПОЛЯ ПЛАТ МИКРОБЛОКОВ ЭЛЕКТРОННОЙ АППАРАТУРЫ
Меркухин Е.Н.1, Омаров О.М.1
1ФГБОУ ВПО «Дагестанский государственный технический университет» Министерства образования и науки РФ, Махачкала, Россия (367015, г. Махачкала, пр. И. Шамиля, 70), e-mail: [email protected]
В статье предлагается модель для расчета температурного поля плат микроблоков электронной аппаратуры и оценка ее адекватности. Модель построена на основе обоснованных допущений и является иерархической. Сначала определяется температура корпуса с использованием известных инженерных методов расчета, а затем рассчитывается температурное поле каждой платы численным методом верхних релаксаций. Предложенная вычислительная формула позволяет проводить расчеты для областей с неоднородными теплофизическими характеристиками. Далее используется электротепловая аналогия для вычисления температуры каждого электронного элемента. Для оценки адекватности модели проведены вычислительные и физические эксперименты. При проведении вычислительных экспериментов исследуется реакция модели на изменение входных данных: координат источника тепла на плате, толщины теплопроводного сердечника платы и диэлектрического покрытия, коэффициентов теплопроводности материалов платы, мощности, рассеиваемой источником тепла, толщины теплопроводной пасты между источником тепла и поверхностью диэлектрического покрытия сердечника платы. По реакции модели сделано заключение о ее адекватности и возможности использования для теплофизических расчетов микроблоков электронной аппаратуры.
Ключевые слова: микроблок, модель, тепловой режим, численный метод верхних релаксаций, электротепловая аналогия, температурное поле платы.
ASSESSMENT OF ADEQUACY OF MODEL FOR CALCULATION TEMPERATURE THE WEEDING PAYMENTS OF MICROBLOCKS OF THE ELECTRONIC EQUIPMENT
Merkukhin E.N.1, Omarov O.M.1
1Dagestan State Technical University" of the Ministry of Education and Science of the Russian Federation, Makhachkala, Russia (367015, Makhachkala, I. Shamil Ave., 70), e-mail:[email protected]
In article the model for calculation of a temperature field of payments of microblocks of the electronic equipment and an assessment of its adequacy is offered. The model is constructed on the basis of reasonable assumptions and is hierarchical. At first case temperature decides on use of known engineering methods of calculation, and then the temperature field of each payment a numerical method of the top relaxations pays off. The offered computing formula allows to carry out calculations for areas with non-uniform teplofizi-chesky characteristics. Further the electrothermal analogy for calculation of temperature of each electronic element is used. For an assessment of adequacy of model computing and physical experiments are made. When carrying out computing experiments reaction of model to change of entrance data is investigated: coordinates of a source of heat on a payment, thickness of the heat-conducting core of a payment and a dielectric covering, coefficients of heat conductivity of materials of a payment, the power disseminated by a source of heat, thickness of heat-conducting paste between a source of heat and a surface of a dielectric covering of the core of a payment. On reaction of model the conclusion about its adequacy and possibility of use for heatphysical calculations of microblocks of the electronic equipment is made.
Key words: microblock, model, thermal mode, numerical method of the top relaxations, elektrotep-lovy analogy, temperature field of a payment.
Введение
Большое разнообразие конструкций и условий теплоотвода не позволяет предложить некую универсальную тепловую модель для детального расчета перегревов электронных элементов. В данной работе предлагается тепловая модель, позволяющая реализовать методику детального расчета температурного поля для микроблочных конструкций электронной аппаратуры.
Цель исследования
Анализ адекватности предлагаемой тепловой модели.
Материал и методы исследования
Конструкция микроблока собирается из типовых конструктивных элементов, каждый из которых представляет собой алюминиевый каркас с закрепленной на нем печатной платой. Печатные платы являются многослойными керамическими и могут иметь теплопроводные медные шины, на которые непосредственно устанавливаются микросхемы, выделяющие наибольшее количество тепла. Кроме того, могут использоваться также платы с теплопроводными сердечниками, покрытыми диэлектриком. Типовые конструктивные элементы складываются в виде этажерки и стягиваются шпильками, образуя корпус микроблока. Более детальное описание конструкции приведено в статье [3]. В такой конструкции большая или значительная часть тепла отводится от источников через элементы конструкции, то есть печатную плату и теплопроводы, а часть путем конвекции. Отводом тепла путем излучения можно пренебречь, так как при рабочих температурах электронных элементов оно незначительное и, кроме того, имеют место переотражения из-за небольших расстояний между платами. Поэтому такое допущение вполне оправданно. Принимается также допущение о том, что перепад температуры по толщине платы незначителен. Принятые допущения позволяют рассчитывать температурное поле платы как двумерную задачу, которая описывается дифференциальным уравнением в частных производных вида:
![]() [
[![]() (x,y)
(x,y)![]() (x,y)] + F(x,Y) - 2
(x,y)] + F(x,Y) - 2![]() c(T(x,y) - Tc)
= 0 (1)
c(T(x,y) - Tc)
= 0 (1)
где ![]() (x,y) -
функция коэффициента теплопроводности; T(x,y) - искомая функция температуры;
F(x,y) - функция, определяющая мощность тепловыделения в каждой точке
области;
(x,y) -
функция коэффициента теплопроводности; T(x,y) - искомая функция температуры;
F(x,y) - функция, определяющая мощность тепловыделения в каждой точке
области; ![]() c - среднее
значение коэффициента теплоотдачи с поверхностей платы; Tc -
средняя температура среды, окружающей плату.
c - среднее
значение коэффициента теплоотдачи с поверхностей платы; Tc -
средняя температура среды, окружающей плату.
На границе области (платы) задаются граничные условия, получаемые после расчета температуры корпуса. В качестве тепловой физико-математической модели корпуса используется макромодель [1], которая позволяет определить интегральные (усредненные) значения температуры корпуса. Для участков границы, имеющих тепловой контакт с корпусом микроблока, задается температура (граничные условия первого рода):
T г =![]() PcкSткRтк
+ Tк , (2)
PcкSткRтк
+ Tк , (2)
где Pcк - доля суммарной мощности, стекающая с платы на корпус за счет кондуктивного механизма теплопередачи; Sтк - площадь теплового контакта платы с корпусом; Rтк - удельное тепловое контактное сопротивление соединения платы с корпусом; Tк - температура корпуса в месте соединения с платой.
Участки границы области, не имеющие теплового контакта с корпусом, считаются теплоизолированными:
![]() (3)
(3)
Уравнение (1) с граничными условиями (2), (3) решается численным методом верхних релаксаций. Вычислительная формула имеет вид:
![]()
![]()
![]() =
=![]()
![]() ,
,
где к -
номер итерации; ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() - значение коэффициента
теплопроводности в узле (i,j);
- значение коэффициента
теплопроводности в узле (i,j); ![]() - средняя
температура корпуса микроблока;
- средняя
температура корпуса микроблока; ![]() температура
в узле (i,j) на к-той итерации;
температура
в узле (i,j) на к-той итерации; ![]() шаг
дискретизации;
шаг
дискретизации; ![]() средняя температура
платы.
средняя температура
платы. ![]()
Параметр релаксации ![]() вычисляется
по формуле [5]:
вычисляется
по формуле [5]:
![]()
где M и N - количество узлов по широкой и узкой стороне области решения (платы).
После расчета температурного поля платы вычисляется температура каждого элемента.
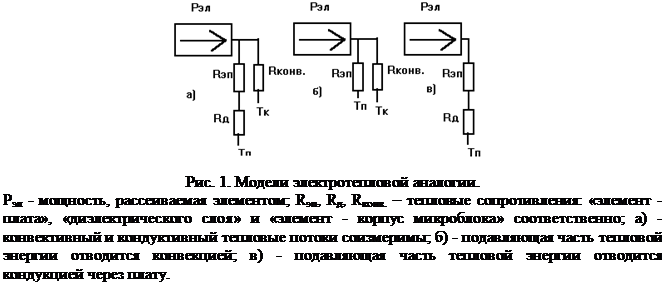
В качестве модели используется электротепловая аналогия. Детальная физическая интерпретация этой модели приведена в [4]. В зависимости от конструктивного варианта исполнения платы и способа установки элементов возможны варианты тепловой модели, представленные на рис. 1.
На основе предложенной модели разработана методика расчета, реализованная в виде пакета прикладных программ. Расчет ведется для максимального количества точек по широкой стороне платы – 100 (сетка 100х100, если плата квадратная). Мощность рассеяния распределяется равномерно по всем узлам, попавшим на посадочное место микросхемы. Каждому узлу сетки приписывается коэффициент теплопроводности. Для узлов, попавших на теплопроводы, рассчитывается коэффициент теплопроводности по формуле (4).
![]() ,
(4)
,
(4)
 где
где ![]() -
коэффициент теплопроводности узла, попавшего на теплопровод;
-
коэффициент теплопроводности узла, попавшего на теплопровод; ![]() - коэффициент
теплопроводности материала теплопровода;
- коэффициент
теплопроводности материала теплопровода; ![]() -
коэффициент теплопроводности материала платы (диэлектрика);
-
коэффициент теплопроводности материала платы (диэлектрика); ![]() - толщина теплопровода;
- толщина теплопровода; ![]() - толщина платы.
- толщина платы.
Результаты исследования и их обсуждение
Для проверки адекватности тепловой модели был проведен ряд вычислительных экспериментов, то есть проводились расчеты для исходных данных, которые целенаправленно изменялись. По результатам расчетов оценивалась реакция модели на изменение исходных данных (параметров конструкции микроблока и источников тепловыделения) исходя из физических закономерностей тепловых процессов. Окончание расчета определяется по максимальной разности температур в точках сетки на текущей и предыдущей итерации. В качестве температуры элемента принимается максимальная температура из всех узлов, попавших на него. Исходные данные для микроблока и платы представлены соответственно в таблицах 1 и 2.
Исходные данные для микроблока Таблица 1
|
Пара-метр |
Вели-чина |
Един. измер. |
Пара-метр |
Вели-чина |
Един. измер. |
Пара-метр |
Вели-чина |
Един. измер. |
Пара-метр |
Вели-чина |
Един. измер. |
|
KONT |
1 |
вариант |
NN |
1 |
шт. |
В1 |
80. |
мм |
UT |
160. |
Вт/°С *м |
|
NV |
1 |
вариант |
D |
3. |
мм |
В2 |
130. |
мм |
EK |
0.4 |
|
|
ТС |
25 |
°С |
G |
0.3 |
Кг |
В3 |
60. |
мм |
RTK |
0.1 |
°С *м2/Вт |
|
РР |
0 |
% |
C |
920 |
Дж/Кг*°С |
Alk |
20. |
Вт/м2*°С |
|
|
|
Исходные данные для платы Таблица 2
|
Пара-метр |
Вели-чина |
Един. измер. |
Пара-метр |
Вели-чина |
Един. измер. |
Пара-метр |
Вели-чина |
Един. измер. |
Пара-метр |
Вели-чина |
Един. измер. |
||||||
|
H |
30. |
мм |
XM |
124. |
мм |
DZ1 |
0.25 |
мм |
UT1 |
160. |
Вт/°С *м |
||||||
|
K1 |
1 |
шт. |
YM |
74. |
мм |
DZ2 |
0.4 |
мм |
UT2 |
1.5 |
Вт/°С *м |
||||||
|
K2 |
0 |
шт. |
RT |
0.001 |
°С *м2/Вт |
DK1 |
0.01 |
мм |
UTK1 |
0.4 |
Вт/°С *м |
||||||
|
IO |
0 |
шт. |
HK |
4. |
мм |
DK2 |
0.01 |
мм |
UTK2 |
0.4 |
Вт/°С *м |
||||||
|
IT |
0 |
шт. |
DX |
1.5 |
мм |
ERRmax |
1E-4 |
°С |
Qmax |
100 |
итерац. |
||||||
|
Alk1 |
0. |
Вт/м2*°С |
Alk2 |
0. |
Вт/м2*°С |
|
|
|
|
|
|
||||||
|
Элемент |
Мощность (Вт) |
Габариты (мм) |
Координаты (мм) |
|
|||||||||||||
|
BX |
BY |
X |
Y |
|
|||||||||||||
|
Микросхема |
1.0 |
7.0 |
10.0 |
62.0 |
37.0 |
|
|||||||||||
Условные обозначения в исходных данных для микроблока и платы:
KONT - вариант теплоотвода от плат (KONT=1 - с четырех сторон); NV - вариант ориентации плат в микроблоке (NV=1 - горизонтальное расположение плат); TC - температура окружающей среды; PP - коэффициент перфорации корпуса микроблока; NN - число плат в микроблоке; D - толщина стенок корпуса микроблока; G - масса микроблока; C - удельная теплоемкость материала микроблока; B1 - высота корпуса микроблока; B2, B3- размеры основания микроблока; Alk - коэффициент конвективной теплоотдачи с поверхности микроблока; UT - коэффициент теплопроводности корпуса микроблока; EK - степень черноты корпуса; RTK - удельное тепловое сопротивление контакта «микроблок – теплосток»; H - расстояние от основания микроблока до платы (при NV=1); K1, K2 - количество элементов с первой и со второй стороны платы соответственно; IO - количество сквозных отверстий в плате; IT - количество теплопроводных шин на плате; XM - больший размер платы; YM - меньший размер платы; RT - удельное тепловое сопротивление контакта «плата - стенка микроблока»; HK - ширина контакта «плата - стенка микроблока»; DX - шаг разбиения платы на дискретное поле; DZ1 - толщина теплопроводного сердечника платы; DZ2 - толщина диэлектрического покрытия теплопроводного сердечника платы; DK1 - толщина клея между диэлектрическим покрытием и теплопроводным сердечником; DK2 - толщина пасты между диэлектрической платой и элементами на ней; ERRmax - максимальная относительная ошибка расчета теплового поля платы, при которой этот расчет прекращается; UT1 - коэффициент теплопроводности теплопроводного сердечника платы; UT2 - коэффициент теплопроводности диэлектрического покрытия теплопроводного сердечника платы; UTK1 - коэффициент теплопроводности клея между диэлектрическим покрытием и теплопроводным сердечником; UTK2 - коэффициент теплопроводности пасты между диэлектрической платой и элементами на ней; Qmax - макс. число итераций расчета теплового поля платы; Alk1, Alk2 - коэффициенты средней конвективной теплоотдачи от элементов, стоящих соответственно с первой и второй стороны платы; X,Y - координаты центра элемента, стоящего на плате по осям X и Y; BX,BY - размеры элемента, стоящего на плате по осям X и Y; мощность - мощность тепловыделения элемента; элемент - условное обозначение элемента.
В процессе вычислительных экспериментов менялись параметры таблицы 2: X,Y; мощность; DK2; DZ1; UT1; DZ2. На рис. 2 приведены результаты изменения температурного поля платы (°С) в зависимости от изменения параметров. Приведенные графики показывают распределение температуры в плоскости сечения, проведенной перпендикулярно поверхности платы через ее центр и параллельно ее большему размеру.
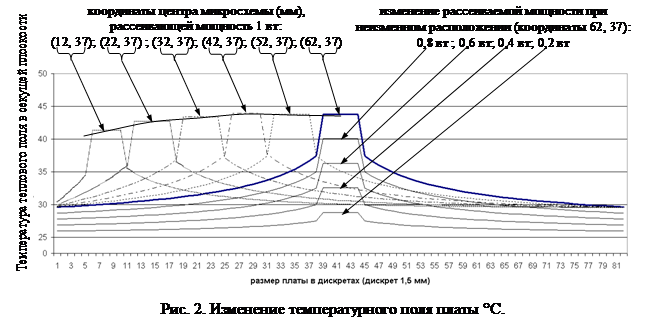 |
Анализ графиков показывает, что модель адекватно реагирует на изменение исходных данных. При смещении источника от центра к краю платы температура падает нелинейно, что согласуется с закономерностью изменения теплового сопротивления от источника тепла до краев платы при изменении координат его расположения Rt(X,Y). Изменение этого сопротивления будет определяться в основном параметрами теплопроводного сердечника платы. Для оценки можно использовать из [2] преобразованную приближенную инженерную формулу (5).
Кривая уменьшения температуры при перемещении источника тепла (рис. 2) не выглядит монотонно убывающей. Это объясняется ошибкой дискретизации, то есть из-за того, что шаг дискретизации (1,5 мм) не кратен размеру источника тепла, количество точек, попадающих на источник, меняется при его перемещении, и поэтому кривая убывания температуры имеет слегка волнообразный вид. Но в целом характер изменения температуры источника аналогичен характеру изменения Rt(X,Y), рассчитанному по формуле (5), что и демонстрирует рис. 3.
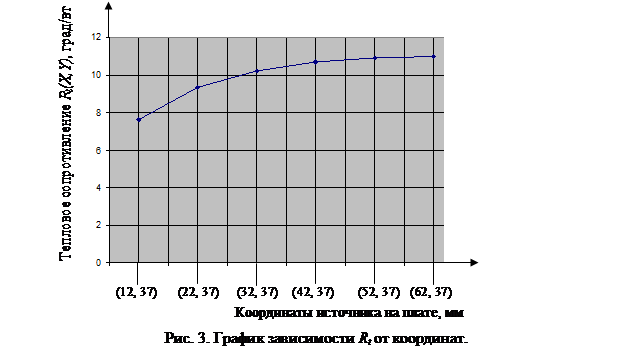
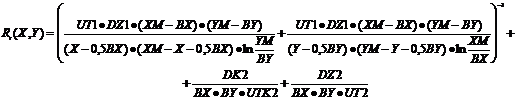 (5)
(5)
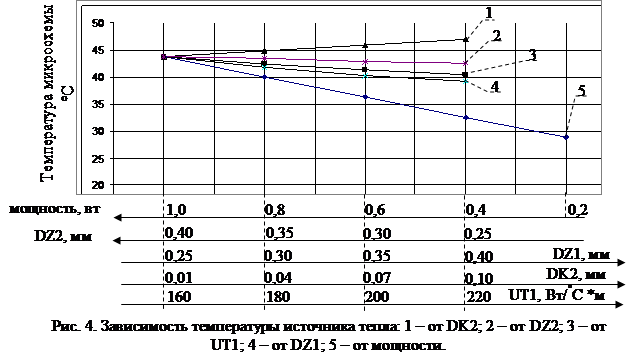
На рис. 4 приведены графики, отражающие зависимость температуры источника тепла от изменения следующих параметров: рассеиваемая источником мощность, DZ1, DZ2, DK2, UT1. Как видно из рисунка, температура источника имеет линейную зависимость при изменении этих параметров, что согласуется с закономерностями теплофизических процессов.
Таким образом, вычислительные эксперименты показывают адекватное поведение предложенной тепловой модели. Экспериментальная физическая оценка точности расчета для реальных микроблоков составила от 15 до 18%. Здесь следует отметить, что повышению точности расчета препятствует проблема достоверности исходных данных, которая пока не имеет решения, то есть невозможно гарантировать значения исходных данных с высокой точностью.
Выводы
Проведенные исследования позволяют сделать вывод о достаточно хорошей адекватности разработанной модели и возможности ее использования для тепловых расчетов микроблоков электронной аппаратуры.
 |
Рецензенты:
Мелехин Владимир Борисович, доктор технических наук, профессор, заведующий кафедрой «Вычислительная техника» ФГБОУ ВПО «Дагестанский государственный технический университет», г. Махачкала.
Кобзаренко Дмитрий Николаевич, доктор технических наук, заведующий лабораторией Информационных технологий в энергетике ФГБУН «Институт проблем геотермии ДНЦ РАН», г. Махачкала.



