Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Введение

В настоящее время при проведении психолого-педагогических исследований широкое применение находят вероятностно-статистические методы. Основы одного из таких методов, позволяющего описать поведение не только большого количества индивидов, но и каждого отдельного индивида при выполнении им той или иной деятельности, например в процессе усвоения знаний учащимся, изложены в работе [1]. Данный метод использует вероятностно-статистическую модель учащегося, в соответствии с которой индивид в процессе обучения идентифицируется функцией распределения (плотностью вероятности), движущейся в информационном пространстве [2]. Это связано с тем, что детерминизм сознания учащегося реализуется через случайность [3], обусловленную внутренне присущим случайным характером психического и соматического состояний индивида. Следовательно, знания учащегося об окружающем мире, являющиеся результатом работы сознания, также несут в себе элементы случайности. Таким образом, указать точное положение учащегося в информационном пространстве не представляется возможным, можно лишь говорить о вероятности нахождения его в той или иной области информационного пространства.

Целью данной работы является экспериментальное исследование вероятностно-статистическим методом поведения студентов в процессе усвоения знаний на протяжении всего периода обучения в высшем учебном заведении.

Индивидуальные функции распределения

Экспериментальные исследования поведения учащихся в процессе обучения проведем, используя вероятностно-статистическое шкалирование [4], в соответствии с которым шкала измерений представляет собой упорядоченную систему , где – некоторое вполне упорядоченное множество объектов (индивидов), обладающих интересующими нас признаками (эмпирическая система с отношениями); – функциональное пространство (пространство функций распределения , где – координата) с отношениями; – операция гомоморфного отображения в подсистему ; – группа допустимых преобразований; – операция отображения функций распределения из подсистемы на числовые системы с отношениями -мерного пространства .

Вероятностно-статистическое шкалирование осуществляется в три этапа: 1) нахождение экспериментально индивидуальных функций распределения (функций распределения, соответствующих отдельным индивидам); 2) отображение функций распределения на числовое пространство; 3) ранжирование учащихся по уровню знаний на основе сравнения моментов различных порядков их индивидуальных функций распределения.

Типичный вид индивидуальных функций распределения, найденных при использовании двадцатибалльной шкалы, представлен на рис. 1. Методика нахождения таких функций описана в [4]. За единицу измерения расстояний в информационном пространстве из соображений удобства и привычности принят 1 балл.

 

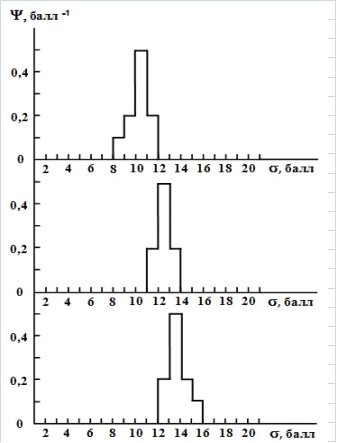
Рис. 1. Типичный вид индивидуальных функций распределения студентов,

получивших на экзамене традиционную оценку «4»

 

Из анализа данных, представленных на рис. 1, следует, что индивидуальные функции распределения, соответствующие разным студентам, находятся в разных областях информационного пространства и отличаются по форме. Однако работать с функциями распределения в функциональном пространстве достаточно сложно. С целью упрощения в [4] предложен переход из функционального пространства в числовое пространство, а именно: каждой из функций распределения ставится в соответствие набор числовых величин – моментов функции распределения от нулевого до бесконечно большого порядка (0, 1, 2, …). Момент нулевого порядка

определяет вероятность найти индивида во всем информационном пространстве и, следовательно, равен единице.

Момент первого порядка

определяет математическое ожидание (среднее значение , координата центра распределения).

Момент второго порядка

характеризует дисперсию функции распределения.

Моменты -го порядка () имеют вид

.

Моменты четных порядков характеризуют расплывание функции распределения, а моменты нечетных порядков – асимметрию функции распределения относительно математического ожидания. Моменты функций распределения могут быть использованы для ранжирования студентов по уровню знаний. В [4] говорится о том, что в большинстве случаев для этой цели достаточно иметь информацию о математическом ожидании (моменте первого порядка), дисперсии (моменте второго порядка) и об асимметрии функции распределения (моменте третьего порядка). Для тонкого ранжирования могут быть использованы моменты более высоких порядков. В табл. 1 приведены типичные значения моментов индивидуальных функций распределения студентов, получивших на экзамене по общей физике традиционную оценку «4».

Анализ данных, представленных в таблице, показывает, что математические ожидания, дисперсии и характер асимметрии индивидуальных функций распределения студентов, получивших на экзамене одинаковую оценку, могут существенно различаться. Это служит основанием для ранжирования студентов по уровню знаний в пределах данной традиционной оценки. Может показаться, что простой переход от пятибалльной шкалы измерений к двадцатибалльной полностью решает проблему ранжирования. Однако это не так, ибо, когда преподаватель на основе традиционного балльного шкалирования ставит, например, оценку «12», то это означает, что знания студента лежат в пределах от 11,5 до 12,5 балла. Фактически студент идентифицируется прямоугольной функцией распределения, имеющей ширину 1 балл, а оценка «12» баллов является по сути дела математическим ожиданием. Такая аппроксимация функции распределения является очень грубой, она искажает истинный вид функции распределения и приводит к ошибке в значениях математического ожидания и дисперсии, а также имеет место потеря информации об асимметрии функции распределения.

 

 

 

Таблица 1

Моменты функций распределения студентов, получивших

на экзамене по общей физике традиционную оценку «4»

 

 

Вместе с тем, когда необходимо провести исследования поведения большого количества студентов (например, студенческого потока) в течение всего цикла обучения на качественном уровне без учета особенностей дисперсии и асимметрии индивидуальных функций распределения, то из соображений простоты анализа целесообразно воспользоваться пятибалльной шкалой измерений и прямоугольной функцией распределения. Тогда, как отмечалось выше, математическое ожидание будет совпадать с оценкой, полученной студентом на экзамене.

Особенности поведения математических ожиданий индивидуальных функций распределения

Проведем сравнение математических ожиданий индивидуальных функций распределения студентов потока одного из технических факультетов Национального исследовательского университета «МИЭТ» после обучения студентов на каждом курсе. По мере приобретения знаний студентом в процессе обучения его индивидуальная функция распределения движется в информационном пространстве, а, следовательно, движется и математическое ожидание. Значение математического ожидания после каждого курса обучения будем находить как сумму математических ожиданий, т.е. фактически как сумму оценок, полученных студентом по всем дисциплинам, а именно:

,

где – математическое ожидание индивидуальной функции распределения студента после сдачи экзамена.

Поскольку на каждом курсе студенты сдают разное количество экзаменов, из соображений удобства анализа перейдем к безразмерным значениям математических ожиданий так, чтобы в каждом случае минимальное значение математического ожидания соответствовало «0», максимальное – «1»:

,

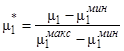где , и – безразмерное, минимальное и максимальное значения математических ожиданий индивидуальных функций распределения соответственно.

На рис. 2 представлен спектр значений математических ожиданий индивидуальных функций распределения после обучения студентов на каждом курсе. Высота линий, соответствующих каждому значению математического ожидания, определяет число студентов, индивидуальная функция распределения которых имеет данное значение математического ожидания. На рисунке представлены также значения математических ожиданий индивидуальных функций распределения (оценок) студентов по их аттестату о среднем (полном) общем образовании, учитывающие такие дисциплины, как математика, физика, химия, литература и русский язык, качество подготовки по которым определяет успешность обучения на техническом факультете.

Из анализа данных, представленных на рис. 2, видно, что основной массе студентов по аттестату о среднем общем образовании соответствуют большие значения математических ожиданий их индивидуальных функций распределения, которые лежат в диапазоне от 0,5 до 1. Однако после первого курса ситуация меняется коренным образом, а именно: теперь уже большинству студентов соответствуют малые значения математических ожиданий, находящиеся в диапазоне от 0 до 0,5. Это обусловлено, вероятно, тем, что студенты еще не успевают полностью адаптироваться к новым для них условиям обучения.

После второго года обучения на спектре математических ожиданий начинают просматриваться три характерные области: область математических ожиданий, соответствующая слабым студентам - от 0 до 0,25; средним студентам - от 0,25 до 0,8 и сильным студентам - от 0,8 до 1. Начиная с третьего курса идет существенное перераспределение численности студентов в пределах спектра возможных значений математических ожиданий так, что после пятого курса основной массе студентов соответствуют значения математических ожиданий, лежащие в диапазоне от 0,5 до 1, т. е большинство студентов по формальным признакам переходят в категорию сильных студентов. Такое поведение математических ожиданий индивидуальных функций распределения хорошо согласуется с поведением функций распределения студенческих потоков, построенных на основе индивидуальных функций распределения [5].

 

 

 

 

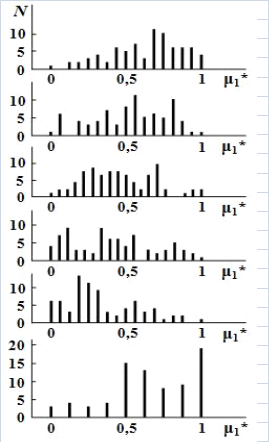
Рис. 2. Связь числа студентов потока с математическими ожиданиями их индивидуальных функций распределения: 1 – после 5 курса; 2 – после 4 курса; 3 – после 3 курса;

4 – после 2 курса; 5 – после 1 курса; 6 – по аттестату о среднем общем образовании

 

Следует отметить, что с третьего курса обучения начинает меняться список учебных дисциплин, а именно: на смену фундаментальным дисциплинам приходят общетехнические и специальные дисциплины. Анализ учебных программ, фактического материала по лекциям, семинарам, лабораторным работам и результатов опроса студентов показал, что уровень фундаментализации общетехнических и специальных дисциплин в большинстве случаев сравнительно низкий. В результате сильные студенты «не дорабатывают», а слабым студентам достаточно простого запоминания материала. Кроме того, как правило, занижаются требования к сдаче экзаменов. Опыт показывает, что именно такая ситуация и является основной причиной увеличения числа студентов на старших курсах, переходящих формально в категорию успевающих на «хорошо» и «отлично».

Выводы

1. Применение вероятностно-статистического метода к анализу поведения студентов в процессе усвоения знаний позволяет на основе сравнения моментов их индивидуальных функций распределения проводить тонкое ранжирование студентов по уровню знаний.

2. Анализ распределения числа студентов по спектру значений математических ожиданий индивидуальных функций распределения после каждого курса обучения выявляет особенности в таком распределении и, следовательно, дает сигнал к необходимости проверки качества обучения и объективности оценки знаний студентов.

Рецензенты:

Евдокимова М.Г., д.п.н., профессор, заведующая кафедрой иностранных языков
ФГАОУ ВПО «Национальный исследовательский университет «МИЭТ», г. Москва.

Романов В.П., профессор, д.ф.-м.н., профессор кафедры общей физики ФГАОУ ВПО «Национальный исследовательский университет «МИЭТ», г. Москва.