В статье [3] приводится разработанная в рамках нелокальной версии термодинамики [2] кинетическая модель расчета многокомпонентной изотермической абсорбции. Уравнение для удельного мольного потока через границу раздела фаз имеет вид
, (1)
, (2)
, (3)
, (4)
где 
- коэффициент массопередачи i-го компонента;
- коэффициенты массоотдачи i-го компонента соответственно в газовой и жидкой фазах.
Для проверки адекватности предложенной модели необходимо произвести расчет и сравнить с имеющимися экспериментальными данными.
Чтобы рассчитать изменение мольного количества распределяющегося компонента в газовой фазе 
по уравнению (1) необходимо это уравнение проинтегрировать
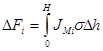, (5)
где 
- поверхность контакта в единице объема, 
,
– рабочая высота аппарата, 
.
На практике интегрирование уравнения (1) сводится к процедуре численного интегрирования. Задача расчета изотермического абсорбера ставится в поверочном варианте. Целью расчета является нахождение выходных потоков абсорбера и их составов, а также покомпонентных составов газа и жидкости по высоте аппарата. Исходными данными для расчета выходных потоков абсорбера и их составов являются: входной поток абсорбента 
, концентрации в нем распределяющихся компонентов 
, количество газа, поступающего на абсорбцию 
, концентрации в нем извлекаемых компонентов 
, величины коэффициентов переноса 
и 
, средние температуры газовой и жидкой фаз 
и 
, константы фазового равновесия извлекаемых компонентов 
, высота рабочей части аппарата , поверхность контакта в единице объема , физические свойства газовой и жидкой фаз (скорость звука, плотность, молярная масса). Решение поставленной задачи осуществляется методом итераций и заканчивается при достижении заранее заданной степени точности. Рассмотрим подробнее последовательность итерационного расчета. Зная высоту рабочей части аппарата и задавшись числом элементарных объемов 
, на которые разбивается рабочая часть аппарата, выбираем шаг интегрирования
.
Так как интегрирование уравнения (1) проводится численно, то изменение мольного количества распределяющегося компонента в газовой фазе 
в j-м элементарном объеме колонного аппарата высотой 
определяется из уравнения (5), записанного в конечных разностях
. (6)
При использовании метода итераций первым этапом расчета является «заполнение» колонны исходным газом. При этом допускается, что до подачи абсорбента в колонну с каждого элементарного объема аппарата уходит газ, по количеству и составу равный сырому газу.
Второй этап решения – расчет каждого элементарного объема аппарата, начиная с верха колонны, в ходе которого определяются количества и составы потоков газа и жидкости, покидающих этот элементарный объем.
Рассмотрим подробнее последовательность расчета j-го элемента аппарата.
1. Определяется удельный мольный поток по уравнению массопередачи (1) .
2. По уравнению (6) рассчитываются изменения мольного количества распределяющихся компонентов в газовой фазе, и эти значения суммируются
.
3. На основе уравнения материального баланса определяются искомые параметры выходных потоков аппарата
,
,
,
.
В результате расчета при первом приближении определяются выходные параметры жидкой фазы 
и расчетные параметры входного газового потока 
. Вследствие произвольного выбора состава газа заполнения полученные в результате первой итерации покомпонентные составы конечных продуктов разделения не удовлетворяют уравнению материального баланса
. (7)
Дальнейший расчет аппарата производится снизу вверх. Если материальный баланс снова не будет сходиться, то расчет аппарата повторяется сверху вниз и снизу вверх до тех пор, пока условие (7) не будет выполнено.
Рассчитаем противоточный абсорбер для разделения многокомпонентной углеводородной смеси. В качестве абсорбента используется керосиновая фракция с молекулярным весом 
и плотностью 
. Количество поступающего на абсорбцию газа 
, количество тощего абсорбента 
, средняя температура жидкости 
, коэффициенты переноса 
, рабочая высота аппарата 
, средняя температура газа 
, удельная поверхность контакта фаз в единице объема 
.
Экспериментальные и расчетные значения концентраций компонентов, а также значения констант фазового равновесия приведены в таблице 1 [4]. Экспериментальные данные заимствованы из работы [1]. Сравнение экспериментальных и расчетных значений выходных концентраций в сухом газе и насыщенном абсорбенте показывает хорошее их совпадение.
Таблица 1
Экспериментальные и расчетные значения концентраций (многокомпонентная углеводородная смесь)
|
Компонент |
Константа равнов. |
Сырой газ (эксп) |
Тощий абсорб. (эксп.) |
Сухой газ (эксп.) |
Сухой газ (расчет) |
Насыщ. абсорб. (экспер.) |
Насыщ. абсорб. (расчет) |
|
|
49,8 |
0,110 |
0,000 |
0,151 |
0,141 |
0,000 |
0,002 |
|
|
11,8 |
0,364 |
0,000 |
0,477 |
0,448 |
0,007 |
0,031 |
|
|
2,7 |
0,211 |
0,000 |
0,240 |
0,216 |
0,053 |
0,076 |
|
|
0,89 |
0,215 |
0,015 |
0,112 |
0,147 |
0,192 |
0,183 |
|
|
0,38 |
0,036 |
0,010 |
0,006 |
0,017 |
0,041 |
0,045 |
|
|
0,28 |
0,047 |
0,042 |
0,010 |
0,025 |
0,113 |
0,074 |
|
|
0,08 |
0,016 |
0,022 |
0,004 |
0,006 |
0,039 |
0,034 |
|
Абсорб. |
- |
0,000 |
0,911 |
- |
- |
0,555 |
0,555 |
Адекватность предложенной кинетической модели реальному объекту была проверена также в ходе экспериментального исследования хорошо растворимого газа в аппарате с достаточно хорошо определяемой поверхностью контакта фаз: исследовалось поглощение аммиака водой из аммиачно-воздушной смеси в трубке с орошаемыми стенками.
В задачу экспериментального исследования входило определение профилей концентраций аммиака в газовой и жидкой фазах по высоте колонны. Изучение поглощения аммиака водой из аммиачно-воздушной смеси проводилось при различных нагрузках по жидкости и газу. Условия проведения эксперимента представлены в таблице 2.
Таблица 2
Гидродинамические условия проведения эксперимента
|
Параметры режима |
1 серия |
2 серия |
|
Расход воды, м3 /c |
|
|
|
Плотность орошения, м3/(м с) |
|
|
|
Изменение скорости газа в колонне, м/с |
|
|
В таблице 3 представлены экспериментальные и расчетные значения концентрации аммиака в газовой и жидкой фазах для плотности орошения 
и различных скоростей газа 
в колонне. Там же приводятся относительные отклонения расчетных значений от экспериментальных.
Таблица 3
Экспериментальные и расчетные значения концентраций аммиака по высоте колонны
|
Скорость газа |
Экспериментальные данные |
Расчетные данные |
|
|
|||
|
|
|
|
|
||||
|
|
0,000 0,002 0,007 0,014 |
0,016 0,025 0,035 0,062 |
0,000 0,002 0,006 0,012 |
0,013 0,022 0,038 0,062 |
0,0 0,0 14,0 14,0 |
18,0 12,0 8,0 0,0 |
|
|
|
0,000 0,004 0,016 0,026 |
0,024 0,034 0,046 0,062 |
0,000 0,006 0,014 0,023 |
0,024 0,034 0,047 0,062 |
0,0 16,0 12,5 11,5 |
0,0 0,0 2,1 0,0 |
|
|
|
0,000 0,008 0,020 0,036 |
0,030 0,038 0,047 0,061 |
0,000 0,009 0,020 0,033 |
0,028 0,038 0,049 0,061 |
0,0 10,0 0,0 8,3 |
6,7 0,0 4,0 0,0 |
|
На рис. 1 представлены изменения концентрации аммиака в жидкой и газовой фазах по высоте колонны для скорости газа 
и плотности орошения 
. Анализ величин, представленных в таблице 3, и графическое сопоставление экспериментальных и расчетных данных об изменении концентрации аммиака в обеих фазах указывают на их удовлетворительное совпадение. Относительное отклонение расчетных значений концентраций от экспериментальных в основном не превышает погрешности схождения материального баланса - 15%.
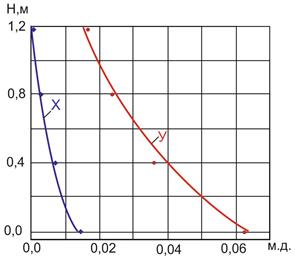
Рис. 1. Распределение концентрации аммиака по высоте колонны в жидкой ( 
) и газовой ( 
) фазах. 
.
При обработке экспериментальных данных коэффициент переноса определялся на основе предположения о том, что перепад концентраций 
происходит на всей толщине жидкой пленки (т.е. толщина пограничного ламинарного слоя в жидкой фазе равна толщине пленки жидкости). Коэффициент переноса в газовой фазе подбирался в ходе расчета до наилучшего совпадения экспериментальных и расчетных данных. В таблице 4 представлены значения коэффициента переноса в газовой фазе и соответствующие ему толщины диффузионного слоя 
в газе в зависимости от скорости газа в колонне для двух различных плотностей орошения.
Таблица 4
Значения коэффициента переноса и толщины диффузионного слоя в газовой фазе
|
Показатель |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Анализ табличных данных показывает, что с увеличением скорости газа в колонне толщина диффузионного слоя в газовой фазе уменьшается, а коэффициент переноса возрастает. Это хорошо согласуется с физическим смыслом, который вкладывается в коэффициент переноса 
.
Подводя итог, можно сделать вывод, что предложенный кинетический метод расчета многокомпонентной изотермической абсорбции, разработанный в рамках нелокальной версии термодинамики, позволяет раскрыть физический смысл коэффициентов массоотдачи и массопередачи, выделить гидродинамическую составляющую этих коэффициентов и поставить на повестку дня разработку теоретических методов определения коэффициентов переноса. Сравнение результатов расчета по предложенной модели с экспериментальными данными для различных случаев абсорбции показывает хорошую ее работоспособность и возможность практического применения.
Рецензенты:
Фокин Владимир Михайлович, доктор технических наук, профессор, заведующий кафедрой «Энергоснабжение и теплотехника» ФГБОУ ВПО «Волгоградский государственный архитектурно-строительный университет», г. Волгоград.
Семенов Борис Александрович, доктор технических наук, профессор, заведующий кафедрой «Промышленная теплотехника» ФГБОУ ВПО «Саратовский государственный технический университет им. Ю.А. Гагарина», г. Волгоград.