Введение

Проблема обеспечения качества электроэнергии является важнейшей проблемой, определяющей надежность и эффективность электроснабжения потребителей [1]. Одним из отрицательных действий некачественной электроэнергии для энергосистем является повышение температуры проводов линий электропередачи, а также обмоток трансформаторов и вращающихся электрических машин выше, которая может превысить допустимый уровень. Сопротивление элементов сети за счет колебания температуры может изменяться примерно на 40 %, а значит, на столько же могут изменяться и потери мощности. Следовательно, при расчете потерь электрической энергии необходимо учитывать температуру нагрева токоведущих частей.

В настоящее время существуют методы учета фактического нагрева токоведущих частей при выборе электрических аппаратов, а также расчета и оптимизации потерь. Однако ни одна из существующих методик не учитывает наличие в сети токов с несинусоидальной кривой, т.е. наличие несинусоидальных режимов. Такие режимы в большинстве случаев являются неэкономичными и могут быть технически недопустимыми. Для решения задач оценки экономичности и допустимости этих режимов, а также для выбора мероприятий по снижению уровня несинусоидальности требуется более точное моделирование элементов сети, нагрузок и источников питания.

Анализ литературы показал, что при расчете потерь мощности фактор нагрева токоведущих частей учитывается редко и только для проводов [2, 3, 4]. Интерес представляет работа по особенностям расчета несинусоидальных режимов электрических сетей методом узловых потенциалов [5]. С помощью этого метода можно рассчитать уровни высших гармоник практически во всех электрических сетях.

Температурная зависимость сопротивления сама не генерирует высшие гармоники, но она может в значительной степени повлиять на распространение гармоник, генерируемых другими источниками. Это влияние будет тем существеннее, чем больше рабочий диапазон температур проводника и соответственно диапазон изменения активного сопротивления.

Для моделирования стационарного или несинусоидального режимов электрических сетей с учетом температурной зависимости сопротивлений элементов этих сетей от параметров режима (нагрева токоведущих частей) необходимы выражения, связывающие электрические и тепловые величины. Эта связь описывается уравнениями теплового баланса.

Рассмотрим эти уравнения применительно к каждому из следующих объектов: масляный трансформатор; сухой трансформатор; кабель, проложенный в земле, и кабель, проложенный в воздухе.

Тепловые процессы в трансформаторах

При работе трансформатора часть электромагнитной энергии превращается в тепло, рассеиваемое в окружающую среду. Главным источником тепла являются сердечник и обмотки, потери в которых составляют примерно 80 % всех потерь.

Теплопередача в трансформаторе осуществляется всеми возможными способами, а именно: путем теплопроводности, излучения и конвекции [6].

Тепловые процессы в кабелях

Для теплового расчета необходимо в общем случае:

1. Составить принципиальную схему замещения тепловых сопротивлений и тепловых потоков, вид которой зависит от конструкции и способа прокладки кабеля.
2. Определить потери в жиле Рж, оболочках Роб и изоляции (диэлектрические потери) Рд кабеля.
3. Определить тепловые сопротивления:
   · изоляции кабеля и его защитных покровов;
   · среды, окружающей кабель.

Выражения, описывающие функциональную зависимость температуры проводников от параметров режима электрической сети для разных ее элементов, как было показано в [7], имеют разный вид, который определяется уравнениями теплового баланса. В простейшем случае при симметричной токовой нагрузке в стационарном тепловом режиме уравнение теплового баланса с учетом теплового действия высших гармоник тока имеет следующий вид:

, (1)

где Iν – действующее значение тока ν-й гармоники, А;

Rν,0 – активное сопротивление току ν-й гармоники при 0 °С, Ом;

A – коэффициент теплоотдачи.

Учитывая тепловое действие высших гармоник тока [7], получим выражения для определения перепада температуры между токоведущими частями и окружающей средой:

1. Для сухого трансформатора

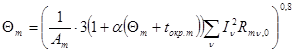; (2)

2. Для масляного трансформатора

; (3)

3. Для кабеля, проложенного в земле

; (4)

4. Для кабеля, проложенного в воздухе

, (5)

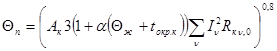где ; (6)

5. Для провода ВЛЭП

. (7)

Из выражений (2–7) следует, что задача расчета температуры нагрева проводников с учетом температурной зависимости является нелинейной. Один из способов решения таких задач – применение численных методов. На современном этапе развития вычислительной техники и программного обеспечения этот способ представляется наиболее оптимальным с точки зрения реализации и получения результатов.

С целью определения влияния фактической температуры токоведущих частей на расчет несинусоидального режима и расчет потерь мощности были проведены соответствующие исследования.

В ходе проводимых исследований ставилась задача оценить степень влияния учета температуры токоведущих частей и высших гармоник на потери активной мощности. Параметры расчетной схемы электроснабжения (рисунок 1) приведены в таблицах 1 и 2.

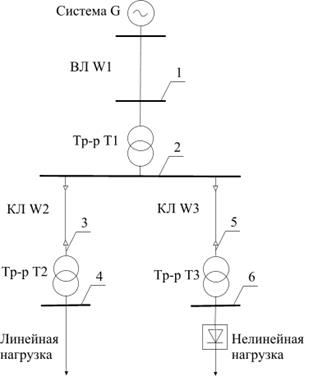
Рисунок 1. Расчетная схема электроснабжения

Таблица 1. Параметры линий

Таблица 2. Параметры трансформаторов

Следует отметить, что неучет фактического нагрева токоведущих частей может приводить к значительным погрешностям при расчете потерь мощности и энергии. Для трансформатора Т3 был проведен вычислительный эксперимент по определению погрешности расчета потерь мощности при учете и неучете температуры (рисунок 2, таблица 3):

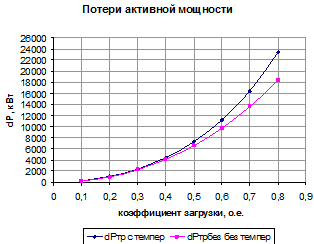
Рисунок 2. Расчет потерь мощности в КЛЭП при учете и неучете температуры

Таблица 3. Расчет погрешности определения потерь мощности

На основании приведенных данных можно сделать следующий вывод: при увеличении коэффициента загрузки погрешность начинает превышать допустимый предел точности 5%. А для данного случая при коэффициенте загрузки трансформатора 0,8 погрешность достигает 21,6 %, что довольно значительно.

Аналогичные зависимости были получены при отличных от указанных выше условий проведения эксперимента, а именно, при прокладке КЛЭП в земле, воздушном типе охлаждения трансформаторов Т2,Т3 и различной температуре окружающей среды в диапазоне от
-25 до +30 °С.

Анализ этих зависимостей показал, что способ прокладки КЛЭП и температура окружающей среды незначительно влияют на характер зависимостей δР=f(kзагр). С возрастанием протяженности КЛЭП и понижением температуры окружающей среды согласно приведенным графикам погрешность расчета возрастает. Таким образом, условия, при которых целесообразно учитывать нагрев токоведущих частей при расчете потерь активной мощности в данной сети, определяются главным образом загрузкой элементов электроэнергетической системы. Вместе с тем длина КЛЭП оказывает существенное влияние на точность расчета. Так, при полной загрузке элементов рассматриваемой расчетной схемы погрешность при длине КЛЭП, равной 0,5 км, составляет 20 %, а при длине 5 км – 35 %. Это означает, что чем более протяженными являются распределительные сети, тем более важным становится учет фактического нагрева токоведущих частей при расчете потерь мощности.

В таблице 4 представлены результаты вычислительного эксперимента, полученные с помощью разработанной программы и содержащие данные численных значений напряжений и токов основной частоты и высших гармоник, а также потери мощности в элементах СЭС.

Таблица 4. Результаты вычислительного эксперимента

Как было показано выше, неучет температуры окружающей среды может также внести определенного рода погрешность в расчет сопротивления. Для оценки этой погрешности был произведен вычислительный эксперимент при изменении температуры окружающей среды от -30 до +20 ºС. Были получены следующие (таблица 5, рисунок 3) результаты для элементов W3 и Т3.

Таблица 5. Расчет потерь при различных температурах окружающей среды

Следует отметить, что диапазон изменения расчета потерь мощности может достигать 20–25 % для кабельной линии и 5–10 % – для трансформатора. На основании этого можно сделать вывод, что учет окружающей температуры для кабельных линий, проложенных в воздухе, и в случае значительных перепадов между зимними и летними температурами обязателен.

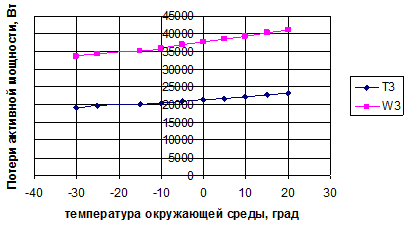
Рисунок 3. Расчет потерь мощности при различных температурах окружающей среды

Выводы

1. Температурная зависимость сама не генерирует высших гармоник, но в значительной степени может повлиять на распространение гармоник, генерируемых другими источниками.
2. Неучет нагрева при выборе мероприятий по снижению потерь может привести к более серьезным ошибкам, чем просто при расчете потерь.
3. Учет нагрева дает возможность уточнить расчетное снижение потерь более чем на 40 %.

Полученные показатели позволяют сделать вывод о целесообразности учета нагрева токоведущих частей при выборе мероприятий по снижению потерь и улучшению показателей качества электроэнергии в сетях промышленного типа.

*Статья опубликована при финансовой поддержке Министерства образования и науки РФ в рамках выполнения соглашения № 14.В37.21.0332 от 27 июля 2012 г.

Рецензенты:

Сидоров О. А., д-р техн. наук, профессор, заведующий кафедрой "Электроснабжение железнодорожного транспорта" ФГБОУ ВПО "Омский государственный университет путей сообщения", г. Омск.

Федоров В. К., д-р техн. наук, профессор кафедры электроники и электрификации сельского хозяйства ФГБОУ ВПО "Омский государственный аграрный университет им. П. А. Столыпина", г. Омск.