Scientific journal

Modern problems of science and education

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

В данной работе изучим поведение некоторых объектов микроэкономикис помощью аппарата теории дискретных марковских процессов. Рассмотрим микроэкономическую систему, которая описывает состояние некоторой фирмы на рынке и может находиться в каждый момент времени в одном из трёх состояний (рисунок 1):

1) фирма выпускает инновационную продукцию, которая не имеет аналогов на рынке и пользуется спросом у потребителей (состояние x0);

2) у продукции фирмы появились аналоги, которые составляют ей конкуренцию (состояние x1);

3) у продукции фирмы появилось значительное число аналогов, которые дешевле и доступнее, она не может больше конкурировать на рынке и нуждается в замене или модернизации (состояние x2).

Обозначим через pi(t), i = 0, 1, 2, вероятность того, что в момент времени t система будет находиться в состоянии i.

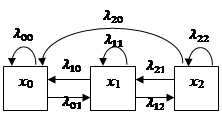
Рисунок 1. Ориентированный граф переходов в различные состояния, – интенсивность переходов из состояния xi в состояние xj, i,j = 0, 1, 2

Цель работы: предложить математические модели, позволяющие вычислять для каждого момента (непрерывного и дискретного) вероятности pi(t), i = 0, 1, 2.

При построении таких моделей будем учитывать характерную особенность рынка: интенсивности переходов из состояния x1 в состояние x0, и из состояния x2 в состояние x0 или x1 равны или близки к 0. Это связано с тем, что с течением времени на рынке всегда появляются аналоги продукции с новыми востребованными потребителями свойствами, и, как правило, они остаются на рынке, конкурируя с продукцией фирмы. Но полностью пренебрегать данными интенсивностями нельзя, так как всегда существует возможность того, что продукция конкурента не будет востребована, в связи с чем ему придётся уйти с рынка.

Пусть вначале время непрерывно. Матрица интенсивностей перехода имеет вид 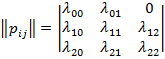[1]:

. (1)

Причем:

(2)

.

Требования (2) необходимы для выполнения условий, предъявляемых к элементам матрицы интенсивностей [1]:

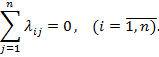
Согласно [1] для определения вероятностей p0(t), p1(t), p2(t) имеем систему дифференциальных уравнений:

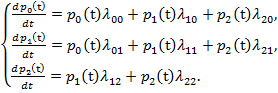(3)

Начальные условия вида , предложенные в [1, 2], не всегда удовлетворяют реальным условиям, складывающимся на рынке товаров, поэтому целесообразнее их задавать в каждом конкретном случае, прибегая к методу экспертных оценок.

Пример 1. Руководство некоторой небольшой фирмы решило выпускать новый недорогой сотовый телефон. Ниша рынка недорогих телефонов заполнена продукцией большого количества фирм-производителей. Продукция данной фирмы является малоизвестной широкому кругу покупателей. Начальные условия для решения (3) задаются экспертами на основе обработки следующего эксперимента. В магазин на продажу выставлен телефон, произведенный фирмой. После обработки статистических данных было установлено, что в среднем из десяти покупателей пятеро интересуются телефоном данной фирмы, трое – выбирают между телефоном рассматриваемой фирмы и телефонами других фирм, аналогичными данному по цене и набору функций, двое – выбирают телефоны известных фирм, не обращая внимания на предложенный товар. Основываясь на этих статистических данных, эксперты предлагают задать для решения системы уравнений следующие начальные условия:

(4)

Матрица интенсивностей переходов из состояния xi в состояние xj, i, j = 0, 1, 2, (единицей измерения времени является неделя) имеет вид:

.

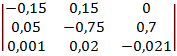Воспользовавшись пакетами прикладных программ «Mathcad», разработанным фирмой ParametricTechnologyCorporation, вычисляем значения вероятностей pi(t), i = 0, 1, 2, численно решая систему (3) при указанных начальных условиях (4) в моменты времени t = 1, 2, … , 40. Результаты вычислений представлены в таблице 1.

Таблица 1. Результаты вычисления pi(t), i=0, 1, 2,t – непрерывно

Графики изменения значений этих вероятностей изображены на рисунке 2.

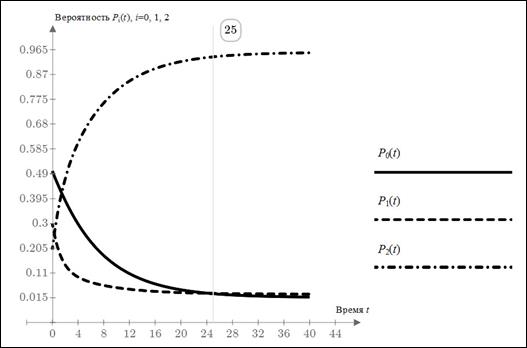
Рисунок 2. Графики изменения pi(t), i=0, 1, 2, при

Как вытекает из данных таблицы 1 и графиков, изображенных на рисунке 2, потеря конкурентоспособности сотового телефона рассматриваемой фирмы с течением времени очень высокая, поэтому фирме не следует выводить свою продукцию на рынок.

Пусть теперь рассматриваемая фирма выводит на рынок абсолютно новый товар, превосходящий по своим характеристикам товары (сотовые телефоны), представленные на рынке. В этом случае начальные условия имеют вид:

а матрица интенсивностей переходов имеет вид:

.

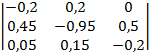Значения вероятностей pi(t), i = 0, 1, 2, найдены численно путем решения системы (3) при заданных условиях в моменты времени , представлены в таблице 2, графики их изменений – на рисунке 3.

Таблица 2. Результаты вычисления значений pi(t), i=0, 1, 2

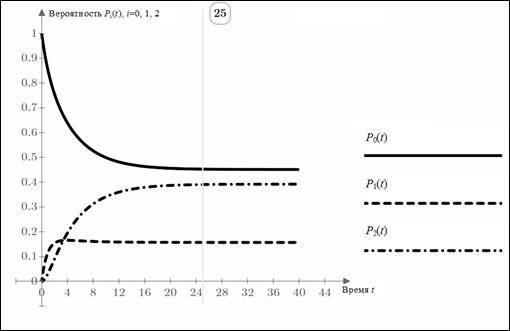
Рисунок 3. Графики изменения значений pi(t), i=0, 1, 2, при непрерывном t

В данном случае продукция фирмы, на момент её выпуска на рынок, является вполне конкурентоспособной, причём с течением времени её конкурентоспособность сохраняется. В связи с этим фирме целесообразно производить и реализовывать данный товар.

Пусть теперь время t является дискретным, t = 0, 1, …, n. Матрица вероятностей перехода из состояния xi в состояние xj, i, j = 0, 1, 2, имеет вид [1]:

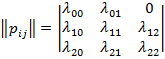. (5)

Тогда за n шагов (в момент t= n) матрица вероятностей перехода будет иметь вид [3,8]:

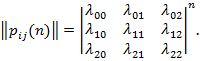(6)

Вектор начальных вероятностей, как и начальные условия для математической модели с непрерывным временем, целесообразнее задавать в каждом конкретном случае, используя метод экспертных оценок.

Пример 2. Фирма выпускает телевизор с новым набором функций, которых не было представлено ранее. Переход из состояния в состояние осуществляется при появлении на рынке конкурирующих товаров. Пусть матрица вероятностей перехода имеет вид:

.

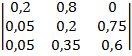В связи с тем, что рынок телевизоров перенасыщен различными моделями крупных производителей, которые хорошо известны потребителям, вектор начальных вероятностей зададим в виде:

Для численного решения воспользуемся пакетом прикладных программ «Mathcad», разработанным фирмой ParametricTechnologyCorporation.

Результаты вычислений представлены в таблице 3.

Таблица 3. Результаты вычисления значений pi(t), i=0, 1, 2 при дискретном времени t перехода из состояния в состояние

Графики изменения значений pi(t), i = 0, 1, 2, представлены на рисунке 4.

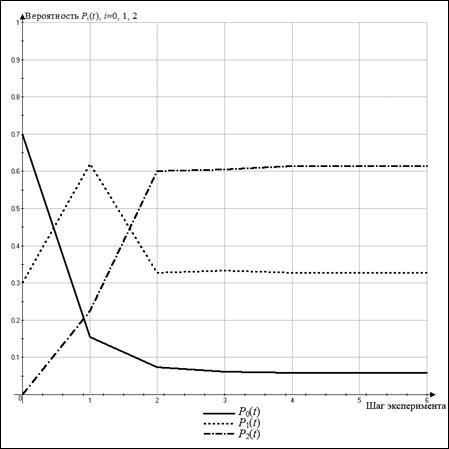
Рисунок 4. График изменения значений вероятностей pi(t) при дискретном t

Как видно из полученных результатов, конкурентоспособность товара значительно меняется при появлении на рынке товаров первых двух конкурентов, после чего значение вероятности p2(t) значительно увеличивается, что указывает на необходимость выпуска более конкурентоспособного продукта.

Заключение

Как показывают результаты вычислительных экспериментов, предложенные математические модели могут применяться для прогноза конкурентоспособности выпускаемого на рынок товара и анализа вопроса о целесообразности его выпуска. Предложенные модели позволяют рассчитать вероятность нахождения экономической системы в каждом из состояний x0, x1, x2. При расчете уровня конкурентоспособности выпускаемой продукции можно успешно использовать оба типа предложенных моделей (с дискретным и непрерывным временем) одновременно.

Рецензенты:

Лебедев Константин Андреевич, доктор физико-математических наук, профессор кафедры прикладной математики ФГБОУ ВПО "Кубанский государственный университет", г. Краснодар.

Приходько Андрей Иванович, доктор технических наук, профессор кафедры общего, стратегического, информационного менеджмента и бизнес-процессов ФГБОУ ВПО "Кубанский государственный университет", г. Краснодар.