Подъемные установки шахт и рудников являются наиболее сложными и энергоемкими объектами в общей технологической цепи транспортировки полезных ископаемых. Существующие методики выбора динамических режимов шахтных подъемных установок ограничивают возможности достоверной оценки этих режимов, что приводит к низкой производительности установок, повышенному расходу энергии, неоправданно большим капитальным затратам на шахтный подъем. Это связано с тем, что [1; 2]:
-
во-первых, рекомендации на проектирование даются не по всему комплексу параметров и показателей, а по отдельным признакам, например по весу полезного груза, по скорости движения, с учетом динамической постоянной подъема, по времени движения и т.д., причем наблюдается большой диапазон значений вышеуказанных рекомендаций у различных авторов;
-
во-вторых, существуют различные подходы при определении константы динамического режима и коэффициента массивности установки;
-
в-третьих, величина, названная механической постоянной времени движения при исследованиях переходных некруговых процессов, некритично используется для исследования замкнутых круговых процессов шахтного подъема;
-
в-четвертых, существующие методики проектирования динамических режимов базируются на абсолютной системе единиц без учета относительных безразмерных параметров и показателей, поэтому не приняты во внимание такие важные характеристики, как импульс действующей силы, импульсное ускорение подъема, относительная скорость движения, относительное ускорение, относительное время движения.
Теоретический анализ динамических режимов подъема весьма трудоемок и требует проведения большого объема экспериментальных исследований. Вместе с тем параметры, определяющие динамику подъема, входят в основные зависимости в составе большого числа параметрических комплексов. Представляется возможным рассматривать основополагающие параметры в виде критериальных комплексов, называемых критериями подобия. Построенные зависимости в виде безразмерных комплексов позволяют предсказать результаты эксперимента, а также проводить исследования на основе моделирования изучаемых явлений. Указанные методы значительно сокращают объемы проектных расчетов, т.к. позволяют оценивать параметры в комплексе в соответствии с критериальными уравнениями, описывающими переходные процессы рудничного подъема.
Так, например, основное уравнение шахтного подъема в критериальной форме имеет вид [1]:
, (1)
где 
относительное усилие на ободе подъемного барабана.
При этом
, (2)
где 
– усилие на ободе подъемного барабана; 
– постоянная составляющая статического усилия; 
– статическая неуравновешенность подъема на данном участке пути; 
– вертикальная высота подъема;
– текущее значение пути движения; 
– относительное ускорение.
Критериями подобия, входящими в это уравнение, являются безразмерные величины: статическая неуравновешенность подъема на данном участке пути 
, относительное ускорение 
.
В исследованиях [1] за критерии подобия также приняты множитель скорости 
; относительное время движения 
; коэффициент асимметрии графика скорости 
; коэффициент 
, учитывающий условия охлаждения двигателя.
В сходственных точках подобных динамических процессов (например, реальный и модельный) данные критерии имеют одно и то же значение и характеризуют подъемную установку как единую электромеханическую систему.
Применяя анализ построенных зависимостей между критериями подобия на основе номограмм подобия, можно не только установить вклад каждого из этих параметров в динамические характеристики подъема, но и получить величины их предельных значений, что необходимо при выборе рационального динамического режима как по энергетическим, так и другим показателям.
Существующие методики проектирования динамических режимов рудничных подъемных установок [5-7] позволяют определить условные минимумы эквивалентных значений усилия и мощности при постоянной массе перемещаемого груза и переменной производительности. При таком подходе остаются неизвестными многие экстремальные показатели переходных режимов, существенно влияющие на эффективность работы рудничного подъема.
Динамический режим электропривода рудничного подъема и других аналогичных электроприводов повторно-кратковременного действия имеет ряд условных и безусловных экстремумов показателей, влияющих на расход энергии, нагрев двигателя, производительность и размеры оборудования [3; 4].
Определить указанные экстремумы динамических режимов возможно, если исследования проводить на основе теории подобия в двух направлениях:
-
при постоянном весе груза и переменной производительности;
-
при переменном весе груза и постоянной (заданной) производительности подъемной установки.
Такой подход позволил установить:
1) условный минимум эквивалентной мощности 
, условный минимум эквивалентного усилия 
, безусловный минимум одноразовых тепловых потерь в двигателе 
в условиях постоянного веса груза 
и переменной производительности 
(рис. 1);
2) безусловный минимум относительной мощности 
, относительные часовые потери тепла в двигателе 
, минимум относительного эквивалентного усилия 
, минимум импульса эквивалентного усилия 
в условиях переменного груза 
и постоянной (заданной) производительности подъемной установки 
.
Указанные показатели позволили на основе критериальных номограмм подобия определить области наивысших КПД при механическом торможении подъемных установок: КПД потерь избытка кинетической энергии при механическом торможении 
(рис. 2); КПД суммы реостатных потерь энергии в период ускорения и потерь избытка кинетической энергии при механическом торможении 
.
Электромеханические процессы шахтного подъема могут быть представлены импульсами сил при разгоне, установившемся движении и торможении, а также импульсным ускорением подъема, импульсным коэффициентом массивности установки, относительной скоростью, относительным временем движения и относительным ускорением подъема [1; 2].
В уравнении импульса действующей силы учитывается время действия силы:
. (3)
В этом случае импульс движущего усилия
, (4)
где 
– импульс движущего усилия при разгоне; 
– импульс движущего усилия при равномерном движении; 
– импульс движущего усилия при торможении.
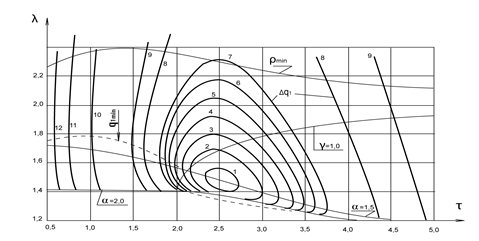
Рис.1. Номограмма изолиний одноразовых потерь тепла при постоянном весе груза и переменной производительности для режимов с механическим торможением
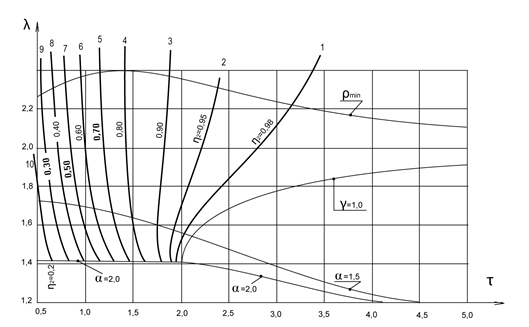
Рис. 2. Номограмма изолиний КПД , учитывающего потерю кинетической энергии при механическом торможении
Импульсный характер переходных режимов исследован при различной степени уравновешенности подъемной установки, т.е. для случаев статически уравновешенной, неуравновешенной и переуравновешенной установок.
При различных графиках скорости возможны еще три вида минимумов импульса движущего усилия:
1) минимум импульса среднеквадратичного усилия;
2) минимум импульса эквивалентного усилия;
3) минимум импульсов сил, формирующихся за счет скорости вращения вала двигателя.
Выбор режимов по минимумам импульсов среднеквадратичного и эквивалентного усилий обеспечивает рациональные показатели динамических режимов, такие как безусловный минимум эквивалентного усилия, безусловный максимум относительной производительности установки, снижение габаритов, веса и расхода электроэнергии.
Выбор режимов по минимуму импульсов сил, формирующихся за счет скорости вращения вала двигателя, возможен не только для любого графика скорости, но и для любой заданной частоты операций.
Номограммы подобия построены на основе критериев подобия для динамических режимов всех видов шахтных подъемных установок – вертикальных, наклонных, уравновешенных, неуравновешенных, с равнобедренными и неравнобедренными графиками скорости, с механическим и электрическим торможением и т.д.
Поскольку номограммы подобия построены по безразмерным показателям, выраженным в относительных единицах, то, проведя простой перерасчет этих показателей в абсолютные единицы, можно выбрать требуемый рациональный динамический режим.
По номограммам подобия выбор динамического режима осуществляется визуально и не по одному какому-либо доминирующему признаку (весу груза, скорости подъема и т.д.), как это традиционно делается, а по всему комплексу критериев, установленных по данным параметрам и показателям.
Таким образом, методы подобия, реализованные в виде номограмм подобия, эффективно решают задачи выбора рациональных режимов работы рудничных подъемных установок.
Рецензенты:
Герц Э.Ф., д.т.н., профессор, декан лесоинженерного факультета ФГБОУ ВПО «Уральский государственный лесотехнический университет» Министерства образования и науки Российской Федерации, г. Екатеринбург;
Кожушко Г.Г., д.т.н., профессор, заведующий кафедрой подъемно-транспортных машин и роботов ММИ ФГОАУ ВПО «Уральский федеральный университет имени первого Президента России Б.Н. Ельцина», г. Екатеринбург.
Библиографическая ссылка
Ляпцев С.А., Двинин Л.А., Двинина Л.Б. ВОПРОСЫ ТЕОРИИ ПОДОБИЯ В ОБЛАСТИ РУДНИЧНОГО ПОДЪЕМА // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17269 (дата обращения: 04.11.2025).