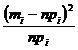Сетевое научное издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 0,936

Модернизация системы образования, происходящая сейчас в российских военных вузах, заставляет по-новому взглянуть на существующую систему обучения. Введение ФГОС-3 требует переосмысления традиционных подходов к образовательному процессу.Новый образовательный стандарт, в отличие от существовавшего ранее ФГОС – 2, предполагает овладение курсантами не толькоопределенным набором знаний, умений и навыков, но еще и совокупностью общих, профессиональных и военно-профессиональныхкомпетенций. Что же такое компетенция? С одной стороны, компетенции определяют требования к уровню подготовки будущего инженера. С другой стороны, компетенция есть совокупность взаимосвязанных личностных качеств (знаний, умений, навыков, способов деятельности), которые необходимы выпускнику для дальнейшей продуктивной деятельности. Таким образом, компетенция является той базовой единицей, которая обеспечивает связь обучения и будущей профессиональной деятельности. Формирование компетенций есть одна из приоритетных задача современного этапа обучения. А уровень сформированности компетенций определяет степень готовности выпускника вуза к несению военной службы.

Каждая дисциплина, изучаемая в вузе, направлена на овладение курсантами определенной совокупности компетенций. Так, всоответствии с ФГОС – 3,дисциплина«Высшая математика»должна формироватьу курсантов следующие компетенции [8,1,2]:

- способность представить современную картину мира на основе целостной системы естественнонаучных и математических знаний (ОК-1);

- владение культурой мышления, способностью к обобщению, анализу, критическому осмыслению, систематизации, прогнозированию, постановке целей и выбору путей их достижения, умение анализировать логику рассуждений и высказываний (ОК-7);

- способность самостоятельно применять методы и средства познания, обучения и самоконтроля для приобретения новых знаний и умений, в том числе в новых областях, непосредственно не связанных со сферой деятельности (ОК-8);

- способность на научной основе организовывать свой труд, самостоятельно оценивать результаты свой деятельности, владеть навыками самостоятельной работы, в том числе в сфере проведения научных исследований (ПК-2);

- способность самостоятельно выполнять научно- исследовательские работы и их отдельные разделы поискового и прикладного характера (ПК-11).

Естественным образом встает вопрос: «Какиесредства необходимо использовать, чтобы сформировать, а затем осуществлять проверкууровня сформированности перечисленных компетенций?» [3,4,5].

Известно, что обучение в математике осуществляется через решение задач. Поэтому,для проверки полнотысформированностикомпетенциймы предлагаем использоватьматематические задачи общей и профессиональной направленности. С позиций деятельностного подхода решение задач есть процесс выполнения действий (мыслительных операций), направленный на достижение цели, заданной в рамках проблемной ситуации — задачи.Следовательно, полнота овладениякурсантами действиямипо решению задачи и определяетуровень сформированности компетенций[6,7].

В своей работе мы определили следующие критерии, по которым оценивается уровень сформированности компетенций:

1 уровень – овладение курсантом отдельно взятым действием. Данный уровень обеспечивается решением задач на применение отдельной математической формулы.

В качестве примера рассмотрим следующую задачу: при определении характеристик рассеивания по дальности артиллерийской системы (случайная величина Х имеет нормальный закон распределения) производится 16 выстрелов со средним квадратическим отклонением равным 8 метрам. Найти доверительную вероятность для статистической оценки математического ожидания, если доверительный интервал .

Для решения задачи необходимо выполнить одно действие – рассчитать показатель функции Лаплассапо формуле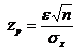 и по таблице найти значение функции Лапласса

2 уровень – овладение курсантом последовательностью взаимосвязанных действий. Данный уровень обеспечивается решением задач, требующим применения не только отдельных математических формул, но и математического метода.

Формулировка такой задачи может быть следующая: в должности начальника отдела технического контроля арсенала ГРАУ произвести выбор артиллерийских снарядов (n = 200) из текущей продукции. Проверяемый размер снаряда измерен с точностью до 1мкм. В таблице 1 приведены отклонения от номинального размера, разбитые на разряды, численности разрядов (сколько штук деталей данного размера попало в разряд) и их частоты– частости.

Таблица 1

Исходные данных задачи

№ разряда i i=1…ℓ	Границы интервала хi…xi+1	mi	P*i
1	-20…-15	7	0.035
2	-15…-10	11	0.055
3	-10…-5	15	0,075
4	-5…0	24	0,120
5	0…5	49	0,245
6	5…10	41	0,205
7	10…15	26	0,130
8	15…20	17	0,085
9	20…25	7	0,035
10	25…30	3	0.015

Оценить с помощью критерия – Пирсонагипотезу о согласии выборочного распределения с законом нормального распределения при уровне значимости .

Алгоритм решения задачи представляет последовательность следующих действий:

1.Выполняем разбиение на разряды по правилу Штюргерса:.

2. Определяемчастости попадания в разряд по формуле:p*i = mi/n.

3.                  Вычисляем границы разрядов исходя из размаха варьирования R:, ширина разряда равна R/k .

4. Определяем по выборке статистические оценки математического ожидания и дисперсии:

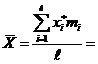
мкм

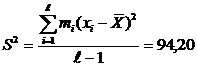мкм2

мкм.

5.                  Вычисляем теоретическую вероятностьрiпопадания отклонений размера деталей в интервалы (хi; xi+1) по формуле:

,

где ,а  - табличная величина.

Результаты вычисленийсводимв таблицу 2.

Таблица 2

Результаты вычислений

i	xi*	zi	1/2 θ(zi)	pi	npi
1	-17,5	-∞	-0,5000	0,0239	4,78	1,04
2	-12,5	-1,99	-0,4761	0,0469	9,38	0,28
3	-7,5	-1,47	-0,4292	0,0977	19,54	1,05
4	-2,5	-0,96	-0,3315	0,1615	32,30	2,13
5	2,5	-0,44	-0,1700	0,1979	39,58	2,24
6	7,5	0,07	0,0279	0,1945	38,90	0,11
7	12,5	0,59	0,2224	0,1419	28,38	0,20
8	17,5	1,10	0,3643	0,0831	16,62	0,01
9	22,5	1,62	0,4474	0,0526	10,52	0,03
10	27,5	2,13	0,4834	-	200
11	-	∞	0,5000	-

6. Находим значениепо формуле: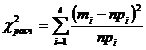=7,09.

            7. Определяем число степеней свободы: (9-й и 10-й разряды объединены).

            8. Находим по входным величинамf=6  и =0,05 табличное значение= 12,6.

            9. Сравниваем значения=7,09 и = 12,6.Так как <, то гипотеза о нормальном законе распределения отклонений от номинального размера не противоречит наблюдениям.

Так образом, решение данной задачи базируется на знании физической сущности ирасчетных зависимостей для вычисления оценок числовых характеристик случайных величин: математического ожидания, дисперсии, среднеквадратичного отклонения, а также порядка проверки правдоподобия гипотезы по критерию Пирсона.

3 уровень – овладение курсантом совокупностью методов и отдельных формульных зависимостей, необходимых для решения конкретной задачи[7,8].

В качестве примера рассмотрим следующую задачу: на испытательном полигоне, в ходе создания макета таблиц стрельбы учитываются факторы воздействия окружающей среды на артиллерийский снаряд. В роли инженера-испытателя оценить характер и величину влияния на движение снаряда в атмосфере, который характеризуется выходным параметром У, трех исследуемых входных факторов: температуры Т0С, давления Р Па, и времени протекания процесса t сек. Задачу исследования решить на основе вычислительного эксперимента с использованием полнофакторного планирования эксперимента и обработки его результатов методом регрессионного анализа.

Процесс решения задачи включает в себя следующие этапы:

1.                  Выполняем мероприятия неформализованного этапа предпланирования эксперимента.На основании изучения априорных данных определяем: центр плана, интервалы варьирования факторов, верхний и нижний уровни факторов, значения которых приведены в таблице 3.

Таблица 3

Результаты априорных данных

Уровни факторов	Факторы в натуральном масштабе
	Т, 0С	Р, 105 Па	t, сек
центр плана или нулевой уровень	150	4	15
интервал варьирования	50	2	5
верхний уровень	200	6	20
нижний уровень	100	2	10

            2. Строим математическую модель процесса вида:

а) для ее построения осуществляем кодирование входных факторов,строим расширенную матрицу планирования полного факторного эксперимента и после рандомизации проводим восемь опытов, результаты которых приведены в таблице 4.

Таблица 4

Результаты опытов

№ опыта	Х0	Х1	Х2	Х3	Х1 Х2	Х1 Х3	Х2 Х3	Х1 Х2 Х3	у
1	+	-	-	-	+	+	+	-	2
2	+	+	-	-	-	-	+	+	6
3	+	-	+	-	-	+	-	+	4
4	+	+	+	-	+	-	-	-	8
5	+	-	-	+	+	-	-	+	10
6	+	+	-	+	-	+	-	-	18
7	+	-	+	+	-	-	+	-	8
8	+	+	+	+	+|	+	+	+	12

б) определяем коэффициенты уравнения регрессии по формуле:

в) врезультате вычислений получаем уравнение регрессии вида:

1.                  Проводим проверку значимости отличия коэффициентов уравнения приближенной регрессии от ноля. Рассчитываем t-критерий Стьюдента 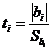, где – точность определения коэффициента  регрессии.

а) для получения дисперсии воспроизводимости эксперимента дополнительно поставим в центре плана три параллельных опыта. Пусть были получены следующие результаты:

б) определяем дисперсию воспроизводимости:

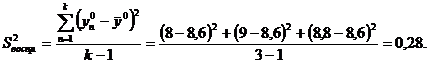
в) в результате расчетов получаем:

г) находим табличное значение критерия Стьюдента, взятое для уровня значимости р = 0.05 и числа степеней свободы f = k-1 = 3-1 = 2 равно: .Таким образом, коэффициенты  незначимы и их из уравнения приближенной регрессии можно исключить, тогда получаем:

4. Проверяем адекватность уравнения регрессии по критерию Фишера: .

а) определяем остаточную дисперсию определяется по формуле:,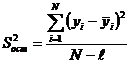

где – число значимых коэффициентов в уравнении регрессии (их четыре)

В условиях примера получим

б) рассчитываем :

в) находим табличное значение критерия Фишера для уровня значимости р=0,05 и чисел степеней свободы .

Так как , то полученное уравнение адекватно описывает процесс.

5.      Проводим анализ уравнения приближенной регрессии и его интерпретацию.

            Для этого проводим анализ модулей и знаков коэффициентов уравнения регрессии. Это даст возможность найти направление изменения исследуемых входных факторов. Затем переходим от кодированных факторов к факторам в натуральном масштабе

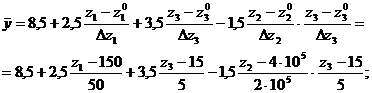
            Полученное уравнение позволит определить (предсказать) выход продукта У при различных значениях температуры, давления и времени протекания процесса.

Как видно из примера, решение задачи основано на выполнении взаимосвязанной последовательностидействий, основанных на знании теории планирования эксперимента ииспользовании различных методов регрессионного анализа и математической статистики.

Таким образом, мы рассмотрели задачи, определяющие различные уровни сформированности компетенций. Результат представлен в таблице 5.

Таблица 5

Уровни сформированности компетенций

Разработанный теоретический аппарат может быть использован не только на занятиях по высшей математике, но и при изучении других дисциплин.

Рецензенты:

Усманов В.В., д.п.н.,  профессор, первый проректор, проректор по научной работе, ФГБОУ ВПО "Пензенский государственный университет архитектуры и строительства", г. Пенза;

ГарькинаИ.А., д.т.н.,  профессор, зам. зав кафедрой "Математика и математическое моделирование", ФГБОУ ВПО  "Пензенский государственный университет архитектуры и строительства", г. Пенза.