Организация движения транспортных потоков, эксплуатационные характеристики как самой лесовозной дороги, так ее отдельных элементов, определяются прежде всего режимом движения лесовозных автопоездов. Основным показателем движения лесовозного автопоезда является тяговое усилие [3].
В рассматриваемом случае динамический фактор вычисляют по формуле:
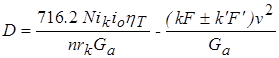, (1)
где 
– мощность двигателя в л.с., зависящая от частоты вращения коленчатого вала двигателя, n (об/мин);
– КПД трансмиссии.
В рассматриваемых условиях можно упростить метод решения уравнения (1) и расширить границы его применения. Это связано с тем, что закономерности изменения мощностных показателей двигателей определяются частотой вращения коленчатого вала для бензиновых двигателей. Для дизельных двигателей 100 % подача топлива отображает внешние скоростные характеристики двигателя, а для любой другой подачи топлива – частные характеристики [4]. На рисунке 1 представлены скоростные характеристики как карбюраторных, так и дизельных двигателей.
Введем координаты относительной мощности 
и относительного числа оборотов 
(
– соответствует , 
– соответствует 
) для объединения характеристики двигателей.
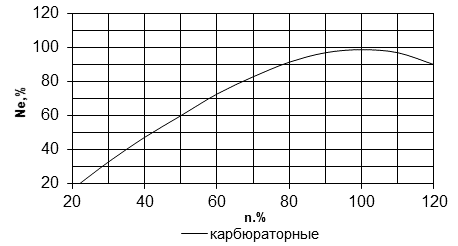
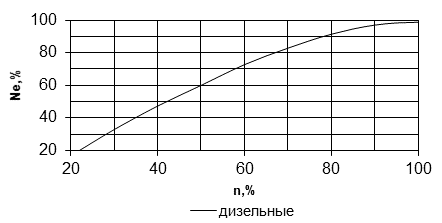
Рис.1. Скоростные характеристики двигателей: n – частота, 
– мощность
На рисунке 2 представлены результаты стендовых испытаний карбюраторных различных двигателей.
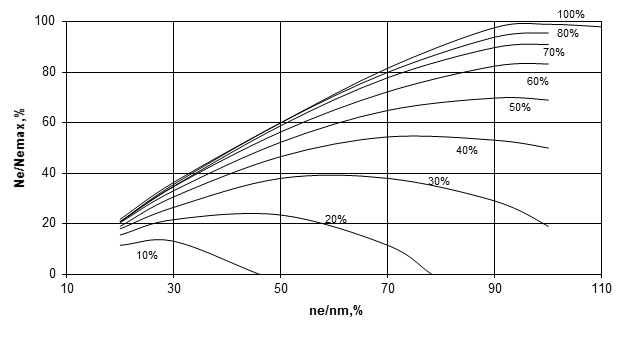
Рис. 2. Относительные частичные скоростные характеристики карбюраторных двигателей
Эмпирические скоростные характеристики, показанные на рисунках 2 и 3, описаны различными зависимостями:
1. Графическими зависимостями, изображенными на рисунке 1.
2. Формулой С.Р. Лейдермана
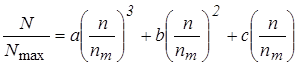, (2)
в которой коэффициенты 
соответственно равны для карбюраторных двигателей – 1; 1; 1, для дизелей – 1; 1,5; 0,5.
3. Формулой Пуансе
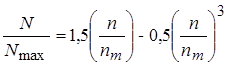. (3)
Из данных формул следует, что для расчета мощности можно использовать следующую зависимость:
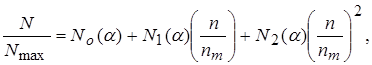(4)
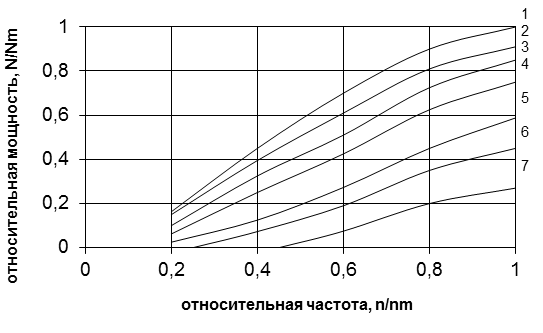
Рис. 3. Относительные скоростные характеристики дизелей в зависимости от положения рейки топливного насоса по сравнению с номинальным: 1-1, 2-0.92, 3-0.86,
4-0.79,5-0.72,6-0.63,7-0.58
В формуле (4) путем статистической обработки относительных частичных характеристик находим коэффициенты 
, а постоянные a и b определяются путём испытания различных двигателей.
Преобразуя формулу (3), уравнение для динамического фактора примет вид:
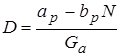. (5)
Согласно формуле (3) не удаётся получить критическое значение скорости, при которой двигатель переходит на пониженные передачи. При 
динамический фактор достигает максимума. В процессе расчёта невозможно определять момент перехода на пониженную передачу. Критические скорости определены для максимальной подачи топлива при полной загрузке лесовозного автопоезда [1].
Второе решение дифференциального уравнения движения лесовозного автопоезда позволяет определить постоянство на всём интервале с помощью коэффициентов a и b в формуле (5). Коэффициенты a и b зависят от степени открытия дроссельной заслонки. Открытие дросселя заслонки непрерывно меняется на участках с изменяющимся продольным уклоном (вертикальные кривые) или участках плана при неизменном уклоне [1].
Поэтому относительные характеристики более эффективно представлять формулой:
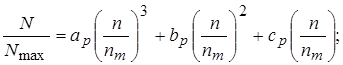(6)
где 
– коэффициенты, индекс 
соответствует степени открытия дроссельной заслонки. Они могут быть получены на основе обработки статистических данных (рисунки 4) при использовании таблицы 1 и 2.
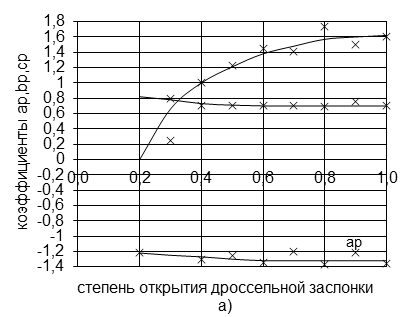
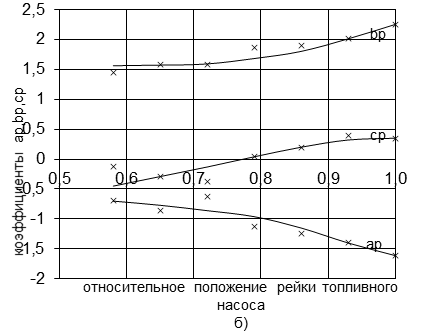
Рис.4. Экспериментальные значения и сглаживающие кривые коэффициентов для карбюраторных (а) и дизельных (б) двигателей лесовозных автопоездов
Таблица 1
Коэффициенты для двигателей с карбюраторами
|
Коэффициенты |
Степень открытия дроссельной заслонки, % |
||||||||
|
100 |
90 |
80 |
70 |
60 |
50 |
40 |
30 |
20 |
|
|
|
-1,32 |
-1,32 |
-1,32 |
-1,32 |
-1,32 |
-1,3 |
-1,27 |
-1,25 |
-1,22 |
|
|
1,62 |
1,6 |
1,57 |
1,48 |
1,38 |
1,21 |
1,0 |
0,66 |
0 |
|
|
0,7 |
0,7 |
0,7 |
0,7 |
0,7 |
0,71 |
0,73 |
0,78 |
0,82 |
Таблица 2
Коэффициенты для дизельных двигателей
|
Коэффициенты |
Относительное, по сравнению с номинальным, положение рейки топливного насоса, % |
||||||
|
100 |
93 |
86 |
79 |
72 |
65 |
58 |
|
|
|
-1,61 |
-1,4 |
-1,15 |
-0,96 |
-0,86 |
-0,77 |
-0,7 |
|
|
2,25 |
2,01 |
1,8 |
1,68 |
1,59 |
1,57 |
1,56 |
|
|
0,35 |
0,32 |
0,2 |
0,04 |
-0,13 |
-0,29 |
-0,45 |
Выразим число оборотов через скорость:
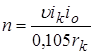, (7)
В результате получаем следующее уравнение для динамического фактора:
, (8)
Решив полученное уравнение, определяем коэффициенты:
, 
, 
,
, 
.
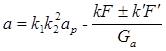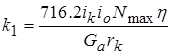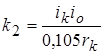Это соотношение позволяет определить критическую скорость в момент переключения с высшей передачи на низшую. Критическую скорость можно определить, если прировнять к нулю производную динамического фактора скорости, то получаем:
. (9)
Моменту переключения с низшей передачи на высшую соответствует скорость 
, которая определяется максимальной частотой вращения коленчатого вала двигателя.
На рисунке 5 согласно формуле (8) представлены динамические характеристики лесовозного автопоезда. Данный рисунок показывает, что скоростные качества на IV и V передачах значительно улучшаются.
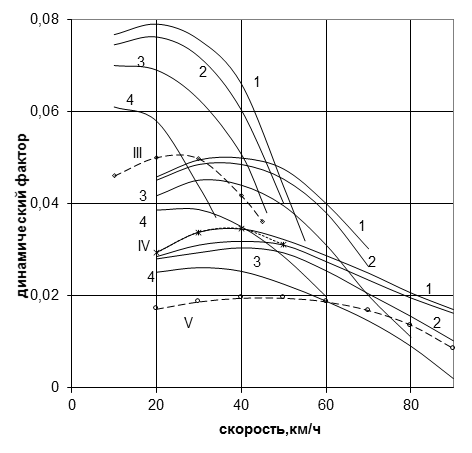
Рис.5. Динамические характеристики автопоезда ЗИЛ-131БА + ГКБ-817 при степени открытия дросселя: 1-1, 2-0.8, 3-0.6, 4-0.4. Пунктир – двигатель 150 л.с., степень открытия дросселя – 1
Полученные таким образом частные динамические характеристики автопоездов, приемлемы для расчета установившихся фактических скоростей на отрезках автодороги с постоянными сопротивлениями.
Подставив 
из формулы (8), получим:
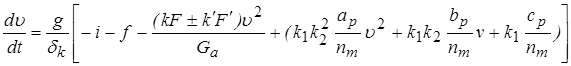, (10)
Частичные динамические характеристики, входящие в уравнение (10), необходимы при проектировании плана и продольного профиля лесовозной дороги при переменных дорожных сопротивлениях и при переменной степени открытия дросселя, при моделировании на ЭВМ движения автопоездов и т.д. [2, 5].
Повысить точности инженерных решений по проектированию лесовозных дорог можно не только с помощью расчета скорости, но и других показателей движения автопоездов. К таким значительным показателям относят затраты по топливу. Он в значительной степени определяет себестоимость перевозок лесоматериалов при выборе оптимального варианта трассы дороги.
Рецензенты:
Пухов Е. В., д.т.н., профессор, зав. каф. эксплуатации машинно-тракторного парка ФГБОУ ВПО «Воронежский ГАУ», г. Воронеж;
Астанин В.К., д.т.н., профессор, зав. каф. технического сервиса и технологии машиностроения ФГБОУ ВПО «Воронежский ГАУ», г. Воронеж.
Библиографическая ссылка
Сушков С.И., Бухтояров В.Н. МЕТОДИКА РЕШЕНИЯ УРАВНЕНИЙ ДВИЖЕНИЯ ЛЕСОВОЗНЫХ АВТОПОЕЗДОВ ПРИ РАЗЛИЧНЫХ РЕЖИМАХ РАБОТЫ ДВИГАТЕЛЯ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=18498 (дата обращения: 04.11.2025).