Сетевое издание

Современные проблемы науки и образования

ISSN 2070-7428

"Перечень" ВАК

ИФ РИНЦ = 1,006

Исследования  климатологов, посвященные антропогенному  потеплению из-за увеличения концентрации   СО2 , свидетельствуют  об изменениях приземной температуры воздуха и осадков. Это влечет за собой изменение условий  естественного увлажнения территорий, отражается на объемах и режимах  речного стока и ирригационной водопотребности и в конечном счете изменяет условия эксплуатации водохозяйственных систем (ВХС). Кроме того, из-за того, что время наступления значимых климатических аномалий сравнимо со временем проектирования  крупных  водохозяйственных объектов,  недоучет подобных изменений может привести к значительным экономическим и экологическим ущербам. Особенно чувствительными к возможным  изменениям климата оказываются ВХС ирригационного назначения. В подобных системах при изменениях климата меняется не только сток, но и водопотребление. Следовательно, для различных сценариев изменения климата задача получения репрезентативных рядов ирригационной водопотребности с межгодовой и внутрисезонной изменчивостью и детальностью, достаточной для проведения водохозяйственных расчетов [6], является актуальной.

   Исследования по этому вопросу представлены в работах [1-4, 7, 8]. Однако их результаты не предназначены для оценки режимов водопотребности с детальностью, необходимой для решения задач регулирования стока.

В [9,10] рассматриваются математические модели продуктивности сельскохозяйственных культур и приводятся оценки изменения их продуктивности  при глобальном потеплении. Оценка оросительных норм и режимов орошения получается в этих моделях как «побочный эффект» при проведении расчетов. Вместе с тем, как отмечают некоторые авторы, подобные модели являются весьма требовательными   к исходной информации гидрометеорологического  содержания.

Анализ различных моделей, приведенный в  [4, 5], позволил выбрать в качестве базовой модель, основанную на методе А.И. Будаговского. Преимущества этого метода обусловлены его универсальностью, выделением в явном виде «климатических» переменных, а также обеспеченностью исходной информацией.

Рассматривается орошаемый массив площадью S, содержащий N культур. Площадь, занимаемая каждой культурой, равна Sn. Для каждой культуры предполагается набор агрофизических параметров и технико-экономических характеристик. Для орошаемого массива задан набор метеорологических характеристик в виде длительных рядов наблюдений с месячной  или декадной разбивкой.

Задача состоит в оценке изменений объемов и режимов водопотребности для различных сценариев изменения климата и определении ущербов, возникающих от недоучета глобальных климатических изменений. Трудности решения этой задачи обусловлены: (1) неопределенностью и значительным временным и территориальным агрегированием сценариев климата; (2) недостаточным количеством параметров, представляемых в сценариях климата; (3) отсутствием репрезентативных рядов наблюдений за водопотребностью земледелия (в целях верификации модели) из-за изменения структуры производства, экономических и агротехнических условий возделывания культур и т.д.

Сформулированная задача решалась для условий Кабардино-Балкарской республики (КБР) за 1944–2004 гг.  и  Лево-Егорлыкской оросительной системы Ставропольского края (ЛЕООС, 1956–1985 гг.).

Рассмотрим  описание метода А.И. Будаговского, ориентированного на расчет режимов орошения и переменных оросительных норм  применительно к оросительной системе.

Оросительная норма является составляющей уравнения водного баланса орошаемых почв, которое можно записать в виде:

где   - запасы воды в корнеобитаемом слое почвы в i-ой камере под j-ой культурой в начале и конце расчетного интервала; Hi –сумма атмосферных осадков в i-ой камере; Oijн - оросительная норма  j-ой культуры в i-ой камере; Еijс- суммарное испарение в  i-ой камере под  j-ой культурой; Qij  - вертикальный водообмен корнеобитаемой зоны почвы с нижележащими слоями или с грунтовыми водами.

Решив это уравнение относительно  Oijн  и принимая во внимание, что Qij = 0 (в начале сезона орошения грунтовые воды залегают глубоко), получаем:

где   

Поскольку в  последнем уравнении величина атмосферных осадков задается по результатам непосредственных наблюдений, то определение оросительных норм сводится к расчетам испарения с орошаемых полей и влагозапасов в почве.

Для определения влагозапасов на конец расчетного интервала времени в почве предложена зависимость:

где   влагозапасы на конец и начало k-ой декады для j-ой культуры  в i-ой камере; продолжительность  k-го  расчетного интервала в днях; mijk, — коэффициенты, подробно описанные в [ 2 ].

Сроки полива определяются (при условии  ≤ ) из последнего уравнения в предположении,  что   : ,

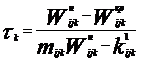 критические влагозапасы, определяемые из

где   испарение за счет транспирации при сомкнутом растительном покрове.

   Поливная норма   определяется:

где   наименьшая  влагоемкость  почвы.

Суммарное испарение определяется по уравнению:

  где  испарение с оголенной почвы; — функция относительной площади листьев  j-ой культуры  в k-ую декаду в i-ой камере, определяемая  ; коэффициент, определяемый:

                            

где   текущие влагозапасы в i-ой камере под j-ой культурой в k-ую декаду ();  — эмпирический коэффициент, зависящий от характера почвы.

  Для оценки испарений за счет транспирации и с оголенной почвы предложены следующие зависимости:

где  переводные множители; определяются по следующим зависимостям:   ,    ,

,

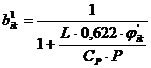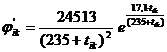где L – скрытая теплота парообразования, равная 600 кал/г; дефицит влажности воздуха, мб;    – скорость ветра на высоте 2 м, м/с;    – радиационный баланс, кал.см-2.мин-1;  – теплообмен в почве, кал.см-2.мин-1;     ,  – интегральные функции характеристик, описывающих тепло и влагообмен в растительном покрове;   – коэффициент турбулентной проводимости слоя воздуха, расположенного между поверхностью почвы высотой 2 м, см/с;  – среднее значение температуры воздуха за рассматриваемый отрезок времени, град;   Р – атмосферное давление, мб; Ср – удельная теплоемкость воздуха при постоянном давлений, кал/г.град.

Оросительная норма – нетто определяется как сумма поливных норм:

.

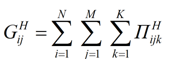Расход воды – нетто (в м3/с) на каждую культуру в выделенной камере для обеспечения заданного полива, определяем по формуле

 ,

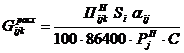где  — площадь i-ой камеры, га;     —  % площади, занятой  j-ой культурой в  i-ой камере;  — продолжительность полива j-ой культуры, сут.; с =a/24 , a — суточная продолжительность полива, час; 86 400 — число секунд в сутках.

Величина                      

характеризует водопотребность системы (региона) в целом в k-ый расчетный интервал времени — укомплектованный гидромодуль.

Ниже приводятся  результаты расчетов режимов орошения и оросительных норм  для различных сельскохозяйственных культур по годам для условий КБР и ЛЕООС (рис. 1-3)  Как видно из рисунков, полученные результаты совпадают с результатами из различных литературных источников.

Вместе с тем были проведены расчеты режимов орошения и оросительных норм при различных сценариях изменений климата и получены соответствующие ирригационные водопотребности для условий ЛЕООС (рис. 4). Полученные результаты свидетельствуют о приемлемости предложенной системы математических моделей для оценки ирригационной водопотребности при антропогенных изменениях климата.

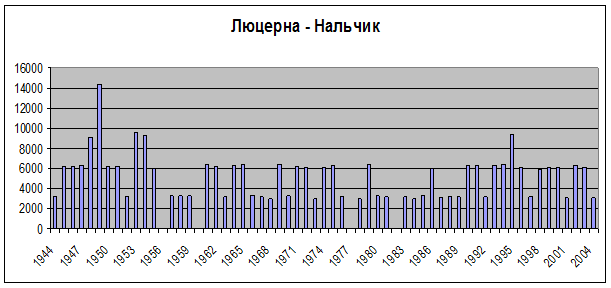
Рис. 1. Оросительные нормы  для люцерны по годам, м3/га, м/с Нальчик

 

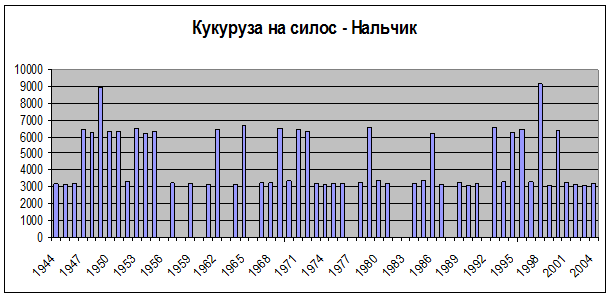
Рис. 2. Оросительная норма  для кукурузы на силос по годам, м3/га, м/с Нальчик

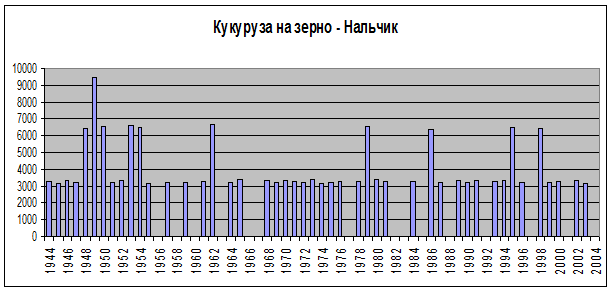
Рис. 3. Оросительная норма для кукурузы на зерно по годам, м3/га, м/с Нальчик

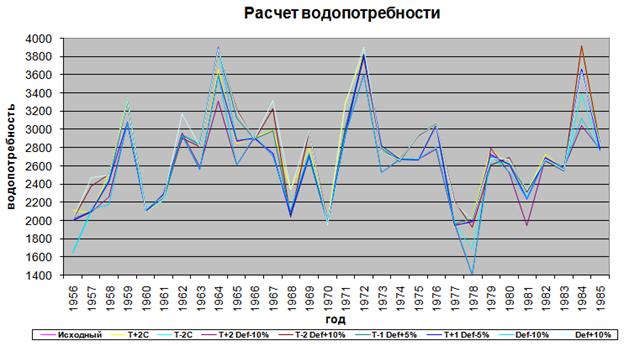
Рис. 4. Ирригационное водопотребление для Лево-Егорлыкской оросительной системы Ставропольского края (1956–1985 гг.)

Рецензенты:

Ашабоков Б.А., д.ф.-м.н., профессор, зав. отделом математических методов   исследования   сложных систем и процессов ФГБУН «Институт   информатики и  проблем регионального управления Кабардино-Балкарского научного центра РАН», г. Нальчик;

 Хачев М.М., д.ф.-м.н., профессор, зав. каф. высшей математики, ФГБОУ  ВПО «Кабардино-Балкарский   государственный аграрный университет  им. В.М. Кокова», г. Нальчик.