Постановка задачи
Исходными уравнениями гидродинамики являются:
– уравнения Навье-Стокса для концентрационной конвекции в приближении Буссинеска
, 
, 
, , 
,
, 
, 
,
- уравнение неразрывности
, , , ,
- уравнения сохранения массы воздуха
,
, , ,
где 
‑ горизонтальные координаты; 
‑ вертикальная координата; t – время; 
‑ расчетная область в плоскости 
, 
‑ граница расчетной области в плоскости ; 
‑ уровень свободной поверхности; T – конечный момент времени; 
‑ вектор скорости течения; 
, 
, 
‑ коэффициенты турбулентного обмена; 
– полное гидродинамическое давление с учетом глубины, 
– плотность; 
‑ концентрация нерастворенного воздуха в виде мелкодисперсных пузырьков; 
– среднее значение концентрации воздуха; 
‑ коэффициент линейной зависимости плотности среды от концентрации воздуха; 
– ускорение свободного падения; 
‑ горизонтальная компонента внешней силы 
, 
‑ скорость всплытия пузырьков.
Источником движения является аэратор 
. Аэратор (рис. 1) находится в плоскости Oxz. Известен расход воздуха 
[м3/с], и скорость движения среды задается: 
, 
, 
, 
, , где – интенсивность расхода воздуха, 
площадь аэратора. Величина потока вещества к нормали поверхности , на единицу площади аэратора она равна 
. Граничное условие для расчета концентрации пузырьков: 
, , , где 
‑ плотность воздуха.
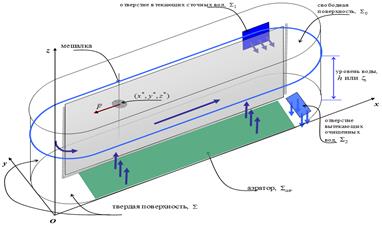
Рис. 1. Схема расчетной области
Отверстие втекания сточных вод 
расположено в стенке параллельной плоскости Oxz. На данной границе задан расход втекающих вод 
, и граничные условия для расчета поля скорости запишутся: , , 
, 
, . Так как пузырьки воздуха не содержатся в сточных водах, то 
, , . На твердой поверхности 
задаются условия прилипания , , 
, 
, и условие не протекания 
, где 
– нормаль. Для вязкой жидкости вопросы правильной постановки граничных условий на участке вытекания 
остаются открытыми. Один из способов задания граничных условий – использование априорных предположений о характере движения жидкости и геометрии рассматриваемой области: , , 
, 
, . Задается сток вещества для расчета концентрации воздуха: 
. На свободной поверхности 
используется динамическое условие: 
, 
, 
, и преобразованное уравнение сохранения массы с учетом кинематического условия на свободной поверхности: 
, , , . Пузырьки воздуха исчезают (аннигилируются), достигнув границы с атмосферой 
, , , .
Дискретная математическая модель
Расчетная область вписана в параллелепипед. Для программной реализации трехмерной математической модели гидродинамики вводится равномерная сетка:
,
где 
– индексы по временной и пространственным переменным 
,
, 
соответственно, 
– шаги по временной и пространственным переменным ,, соответственно, 
– длина расчетной области по временной и пространственным переменным , соответственно, 
– количество узлов по временной и пространственным переменным ,, соответственно.
Для решения задачи гидродинамики использовался метод поправки к давлению [1]. Вариант данного метода в случае переменной плотности примет вид:
,
,
, (1)
,
, 
, 
,
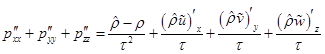где – компоненты вектора скорости, 
,
– компоненты полей вектора скорости на «новом» и промежуточном временных слоях соответственно, 
, 
и 
– распределение плотности водной среды на новом и предыдущем временных слоях соответственно.
При решении поставленной задачи использована декартова система координат в горизонтальной плоскости и σ – координатная система в вертикальном направлении [2; 3; 12]: 
, 
, 
, 
, здесь 
на свободной поверхности, 
на дне; 
общая глубина до свободной поверхности, h=h(x,y) – глубина водного объекта, 
– возвышение свободной поверхности относительно уровня невозмущенной жидкости.
Для описания транспорта пузырьков использовано уравнение диффузии-конвекции, которое в σ-координатной системе запишется следующем виде:
.
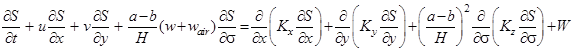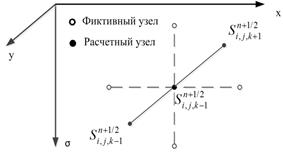
Для решения поставленной задачи транспорта веществ использованы схемы расщепления на одномерную и двумерную задачи, при этом первая подзадача представлена одномерным уравнением диффузии-конвекции-реакции относительно расчетного временного слоя. Шаблон, который будет использоваться при решении данного уравнения на первом полушаге, приведен на рис. 2. Относительно расчетного временного слоя данный шаблон является трехточечным.
|
Рис. 2. Шаблон, который используется для первой подзадачи |
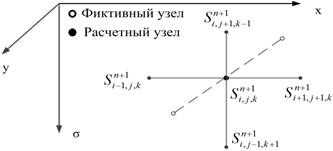
Рис. 3. Шаблон, который используется для второй подзадачи |
Шаблон, который будет использоваться при решении данного уравнения на втором полушаге, приведен на рис. 3. Для аппроксимации задачи по пространственным переменным вводятся коэффициенты 
, 
, 
, 
, 
, 
, 
, описывающие «заполненность» областей, находящихся в окрестности ячейки (контрольных областей). В случае граничных условий третьего рода 
, где n – вектор нормали, направленный внутрь области, дискретные аналоги операторов конвективного 
и диффузионного 
переноса, полученные при помощи интегро-интерполяционного метода [5], учитывающие частичную «заполненность» ячеек, могут быть записаны в следующем виде [9]:
, (2)
.
Погрешность аппроксимации математической модели равна 
, где 
. Доказано сохранение потока на дискретном уровне разработанной гидродинамической модели, а также отсутствие неконсервативных диссипативных слагаемых [10], полученных в результате дискретизации системы уравнений. Достаточное условие устойчивости и монотонности разработанной модели определяется на основе принципа максимума [5] при ограничениях на шаг по пространственным координатам: 
, 
или 
, где 
– числа Рейнольдса, 
– характерный размер области, 
. Дискретные аналоги системы уравнений решаются адаптивным модифицированным попеременно-треугольным методом вариационного типа [4; 6].
Численные эксперименты по моделированию транспорта кислорода в аэротанке
Разработано программное обеспечение, предназначенное для численной реализации прогностических моделей транспорта кислорода в биологических очистных сооружениях. Производились численные эксперименты по моделированию распространения кислорода.
Исходными данными модели являются: скорость всплытия пузырьков 
; диаметр пузырьков 
; ρair = 1,2 кг/м3; ρ = 1000 кг/м3; σ = 0728 Н/м. Параметры расчетной области: длина 120 м, ширина 9 м, глубина 6 м. Результаты численных экспериментов приведены на рис 4. Расчетный интервал составлял: а) 15 мин, б) 30 мин, в) 45 мин, г) 1 час. Для верификации разработанного программного комплекса был проведен численный эксперимент по моделированию транспорта взвеси в водоеме с однонаправленным течением [7; 8].
При этом в инженерных расчетах зависимости ширины зоны смешения от расстояния до створа вычисляют по эмпирической формуле [11]:
, 
. (3)
На рис. 5 приведены зависимости ширины зоны смешения B, м от расстояния до створа L, м (влияние конвективного переноса), рассчитанные на основе разработанного программного комплекса (на рисунке показаны кружками) и на основе формулы (3) (показаны линией).
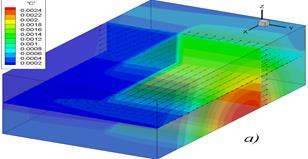
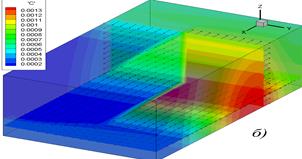
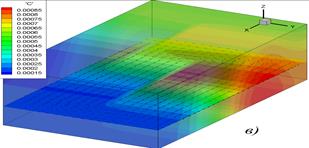
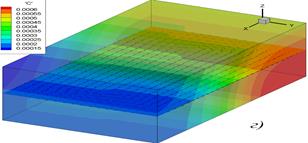
Рис. 4. Динамика изменения концентрации кислорода
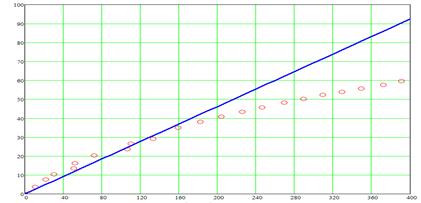
Рис. 5. Зависимости ширины зоны смешения от расстояния до створа
Из результатов расчетов видно, что в случае расстояния до створа 150 м и менее можно принять гипотезу о том, что интенсивность диффузионного перемешивания зависит линейно от интенсивности конвективного переноса и составляет ~23,1% (tg13°). При больших расстояниях преобладание конвективного переноса над диффузионными процессами усиливается.
Работа выполнена при частичной финансовой поддержке Задания № 2014/174 в рамках базовой части государственного задания Минобрнауки России, а также при частичной финансовой поддержке РФФИ по проектам № 15-01-08619, 15-07-08626 и 15-07-08408.
Рецензенты:
Сухинов А.И., д.ф.-м.н., профессор, декан факультета физики, математики и информатики, ТГПИ им. А.П. Чехова (филиал) РИНХ, г. Таганрог;
Илюхин А.А., д.ф.-м.н., профессор, профессор кафедры математики, ТГПИ им. А.П. Чехова (филиал) РИНХ, г. Таганрог.
Библиографическая ссылка
Бузало Н.С., Ермаченко П.А., Проценко Е.А., Хачунц Д.С., Чистяков А.Е. ТРЕХМЕРНАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ДИНАМИКИ ЖИДКОСТИ И КОНЦЕНТРАЦИИ ВОЗДУШНЫХ ПУЗЫРЬКОВ В КАРУСЕЛЬНОМ АЭPОТЕНКЕ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=19511 (дата обращения: 04.11.2025).