Одним из важнейших качеств, позволяющих человеку приспособиться к жизни, является креативность. От понимания механизмов функционирования и развития креативности, во многом зависит жизненный успех учащихся. Поэтому от современного образования требуется уже не фрагментарное включение методов развития креативности в образовательную практику, а целенаправленная работа по развитию креативности. Однако проблема обучения творчеству является чрезвычайно сложной. Для творчества нужна большая самостоятельность учащихся, которую они часто не в состоянии проявить. Если же педагог будет оказывать существенную помощь учащимся при решении творческих задач (давать многочисленные подсказки), то творчества в этой деятельности уже не останется. Один из путей управления творчеством – это сведение творческого мышления к некоторому его упрощению – дивергентному мышлению, введенному в научный обиход Дж. Гилфордом [3]. Дивергентное мышление определяется Дж. Гилфордом как «тип мышления, идущий в различных направлениях». Методистами высказывается мысль, что задача развития дивергентного мышления является более прогнозируемой и более поддающейся педагогическому влиянию, чем задача развития творческого мышления. Так А.Н. Иванов считает, что подобная работа, связанная с развитием дивергентного мышления, будет полезна как раз не столько одаренным детям (уровень креативности которых и так высокий), а тем детям, у которых уровень креативности «средне-нормальный» и даже недостаточный [6].
Целью исследования, описанного в статье является разработка приемов и средств дивергентного развития учащихся при обучении геометрии.
Основное содержание статьи
Дивергентное мышление учащихся целесообразно развивать в процессе обучения математики при решения задач. Мы считаем, что организовывать целенаправленную деятельность по развитию дивергентного мышления целесообразно при работе на первом этапе решения задачи – анализе текста задачи. Это можно объяснить следующими соображениями: большинство исследователей мышления считают, что дивергентное мышление особенно активно работает на начальных этапах решения проблемы. А.Н. Поддьяков, например, выделяет две стадии решения исследовательской задачи: дивергенцию и конвергенцию [9]. Дж. К. Джонс выделяет три стадии решения конструкторско-проектировочной задачи: дивергенцию, трансформацию и конвергенцию [5]. Методистами по математике обычно выделяются четыре этапа решения математической задачи [7]: 1) анализ текста задачи; 2) составление плана решения задачи; 3) реализация плана, 4) проверка решения задачи.
Мы считаем, что и при решении математической задачи дивергентное (расходящееся) мышление особенно активно работает на первом этапе решения, т.е. на этапе анализа текста задачи. А на втором этапе – формулировке плана решения задачи – возникает уже первичная конвергенция (схождение к чему-то одному), которая продолжается на последующих этапах решения задачи.
В ходе нашего исследования мы пришли к выводу, что одним из механизмов развития дивергентного мышления является целенаправленное обучение учащихся перецентрированию. В научный обиход термин «перецентрирование» ввел гештальтпсихолог М. Вертгеймер [2]. Гештальтпсихологи считают, что если при репродуктивном мышлении человек ищет в памяти те приемы, которые способствуют решению, то при продуктивном мышлении у него должно возникнуть понимание проблемы. При этом открытие решения задачи возникает в порядке инсайта, как результат перецентрирования, трансформации самой проблемной ситуации. Сходные идеи высказывались и другими авторами. Так Ж. Пиаже ввел термин «децентрация». Ж. Пиаже изучал ошибки, которые совершали дети при решении предлагаемых им интеллектуальных заданий [11]. То, что эти ошибки постепенно изживались благодаря специально организованной деятельности, он объяснял процессом децентрации. Децентрацией он назвал преодоление тенденции к сосредоточению внимания на единичной, бросающейся в глаза особенности предмета, и появление способности принять во внимание другие существенные особенности этого предмета.
А.А. Брудный вводит понятие «перецентровки», как одного из механизмов понимания информации [1]. При перецентровке структура отражаемой в тексте ситуации предстает в изменяющемся виде, т.е. происходит изменение изначальной структуры текста, смещение центра с одного акцента на другой. Она дает возможность взглянуть на тему под другим углом, увидеть новые связи между теми же понятиями, а значит и новые смыслы.
Наше исследование показало, что существует ряд математических задач, при решении которых можно наблюдать четко очерченный момент изменения направления мыслительной деятельности, который мы и назвали перецентрированием. Человеку бывает непросто совершить перецентрирование, для этого требуется преодоление определенного психологического барьера. Перецентрирование легче осуществлять людям, которые получили возможность поупражняться в этом занятии. Мы разработали систему задач на материале планиметрии 7 – 9 классов, выполняя которые учащиеся смогут получить опыт перецентрирования. Это облегчит им в дальнейшем возможность производить перецентрирование в процессе решения различных задач. Вообще говоря, решение практически любой достаточно сложной задачи по планиметрии, как и по любому другому предмету, способствует развитию дивергентного мышления, т.к. в процессе такого решения происходит неоднократное изменение направления мыслительной деятельности. Но при решении многих задач учителю бывает сложно управлять ходом мыслей учеников. Мы же разработали задания, при решении которых в определенные моменты можно организовать процесс перецентрирования ученика. Эти задания мы так и назвали – задачи на «перецентрирование».
Однако в ходе нашего исследования мы выяснили, что при решении задач по планиметрии происходит дивергенция разных видов. Для успешного решения задач нужно овладеть дивергенцией каждого вида. Но для этого необходимы не просто задачи на «перецентрирование», а система таких задач. Это согласуется с современными воззрениями методистов. Различные ученые сходятся к мысли, что ни одна задача, решаемая изолированно, не дает желаемого результата, не позволяет добиться общей цели. Необходимо учитывать не только особенности каждой конкретной задачи, но и ее место среди других задач, выявлять вклад данной задачи в достижение поставленной цели, иными словами, необходимо организовать задачи в систему. Организация задач в систему рассматривалась различными авторами (С.П. Поленкова, Г.В. Дорофеев, Н.Г. Килина, Г. И. Саранцев, Т.М. Калинкина, И.И. Зубова, В.П. Радченко, Ф.М. Юнусов, В.В. Гузеев, И.В. Кононенко, Л.Д. Белова).
Наиболее удачным нам представляется определение О.Н Орлянской, которая под системой задач понимает совокупность упорядоченных и подобранных в соответствии с поставленной целью задач, действующих, как одно целое, взаимосвязь и взаимодействие которых приводит к заранее намеченному результату [8]. В нашем случае результатом является развитие дивергентного мышления учащихся в процессе обучения их анализу текста задачи. При разработке системы задач на «перецентрирование» мы руководствовались основными принципами: полнота системы, иерархичность системы, связность системы, определенная последовательность задач в системе.
Полнота системы в нашем случае проявляется в наличии задач на все виды дивергенции, происходящей при анализе текста задачи. В ходе нашего исследования мы пришли к выводу, что на этапе анализа текста задачи по планиметрии происходит всего четыре различных вида дивергенции.
Первый вид дивергенции возникает при анализе словесной формулировки задачи. При работе с формулировкой мы ищем различные способы переформулировать условие и требование задачи, выявляем различные значения и смыслы понятий, входящих в формулировку, выводим различные следствия из того, что дано и т.д. Чем больше направлений мысли при этом возникнет, тем больше шансов на успех в решении задачи.
Второй вид дивергенции возникает при анализе чертежа (это может быть и данный чертеж, и чертеж, выполненный нами по словесной формулировке). При работе с чертежом мы стремимся вычерпать всю возможную информацию из чертежа. Мы рассматриваем чертеж под разными углами зрения, выявляем различные связи и отношения, в которых находятся изображенные фигуры, пробуем делать различные дополнительные построения и т.д. Поэтому при работе с чертежом тоже нужна активная дивергенция.
Третий вид дивергенции возникает при анализе фигуры, описанной в задаче, на предмет ее существования. В тот момент, когда человек, стремящейся выполнить требование задачи задумывается над вопросом, а существует ли описанная в задаче фигура, происходит дивергенция, поскольку человек мыслит уже в другом направлении.
Четвертый вид дивергенции возникает при анализе фигуры, описанной в задаче, на предмет ее единственности. При переходе от одной ситуации, к которой применимо условие задачи, к другой ситуации, к которой оно также применимо происходит дивергенция, поскольку человек мыслит в разных направлениях.
Иерархичность системы означает, что наша система состоит из нескольких подсистем, каждая из которых в свою очередь является системой, обладающей свойством полноты. В нашей системе четыре подсистемы (каждому виду дивергенции при анализе текста задачи соответствует своя подсистема).
Рассмотрим в качестве примера подсистему, соответствующую второму виду дивергенции – дивергенции при анализе чертежа. Для того чтобы проанализировать сложный чертеж, получив всю возможную информацию из чертежа, человеку требуется способность к перецентрированию, связанному с возможностью изменять точку зрения на чертеж. Используя психологическую терминологию можно сказать, что в процессе анализа чертежа человек выделяет различные объекты из фона [4]. В рамках психологии установлено, что когда человек смотрит на что-либо, воспринимаемая реальность разделяется как бы на два слоя: на объект и на фон. При этом объект воспринимается как конкретное, четко очерченное замкнутое целое, а фон – как нечто более аморфное, неопределенное. Причем, соотношение объекта и фона – это соотношение динамическое. То есть то, что в данный момент в процессе восприятия чертежа относится к фону, может через некоторое время стать объектом, и наоборот, то, что было объектом, может стать фоном.
В ходе нашего исследования мы пришли к выводу, что можно выделить три вида объектов, которые выделяются из фона при работе с чертежом: геометрические фигуры; геометрические фигуры, находящиеся в некотором отношении с данной геометрической фигурой; пары геометрических фигур, находящихся в некотором отношении между собой.
Для того чтобы учащиеся научились анализировать чертеж в процессе решения задач, необходимо чтобы они получили опыт перецентрирования при выделении из фона объектов каждого из трех видов. Поэтому естественно выделить три вида заданий на выделение объектов из фона.
Вид 1. Задания на выделение в качестве объектов различных геометрических фигур заданного типа.
Пример № 1. Найдите на чертеже 3 параллелограмма (рис. 1).

рис. 1.
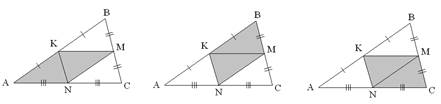
рис. 2.
В данном примере необходимо выделять из фона параллелограммы. Организовать работу с данным заданием можно следующим образом: учащиеся получают карточки с тремя одинаковыми чертежами. Выделенные из фона фигуры они заштриховывают, используя для каждой следующей фигуры новый чертеж, как показано ниже (рис. 2).
Вид 2. Задания на выделение в качестве объектов различных геометрических фигур заданного типа, находящихся в определенном отношении с данной фигурой.
Пример № 1. Найдите на чертеже 4 многоугольника, описанных около окружности (рис. 3.).
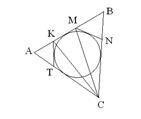
рис. 3.
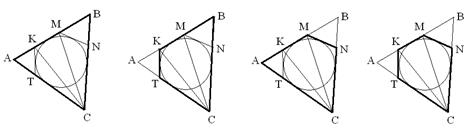
рис. 4.
В данном примере данной фигурой является окружность, а выделять из фона необходимо многоугольники, но не все – а только те, которые находятся в определенном отношении с данной фигурой, а именно: описанные около окружности. При работе с подобными заданиями учащиеся могут не заштриховывать, а обводить контуры выделенных из фона фигур, как показано ниже (рис. 4).
Вид 3. Задания на выделение в качестве объектов различных пар геометрических фигур заданного типа, находящихся в определенном отношении.
Пример. Найдите на чертеже 8 пар равных треугольников (рис. 5).
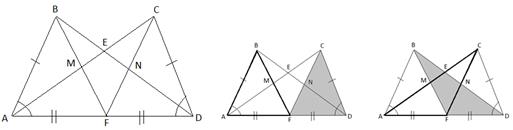
рис. 5. рис. 6.
В данном примере выделять из фона необходимо треугольники, находящиеся в определенном отношении, а именно: в отношении равенства. Фигуры, которые необходимо выделить из фона, могут пересекаться. Поэтому удобно одну из них заштриховать, а у другой выделить контур, как показано ниже (рис.6).
Еще одним принципом, которому должна удовлетворять система задач на «перецентрирование» является связность. Связность системы означает, что вся совокупность задач может быть представлена связным графом, в узлах которого – основные задачи, выше них подготовительные и вспомогательные, ниже – следствия, обобщения и т.д.
Для развития дивергентного мышления используется, прежде всего, основная задача – это достаточно сложная задача, при решении которой наблюдается момент перецентрирования. Однако основной задачи недостаточно, поскольку взятая изолированно она вызывает ряд проблем. Для решения этих проблем используется набор задач, сопутствующих основной задаче. Сопутствующие задачи можно разделить на следующие типы: мотивационная задача, задача на актуализацию знаний, подготовительная задача, вспомогательная задача.
Прежде всего, для решения основной задачи требуется высокий уровень мотивации. Для формирования необходимого уровня мотивации используется мотивационная задача – задача, связанная по содержанию с основной задачей и призванная вызвать интерес к основной задаче. Мотивационная задача может быть привлекательной для учащихся по разным причинам, например, за счет того, что она связана с их субъектным опытом, или же в процессе ее решения привлекается материал по психологии, рассматривается некоторое противоречие, рассматриваются разные мнения по одному и тому же вопросу и т.д. Важно чтобы мотивационная задача казалась учащимся несложной. Мотивационная задача предлагается обычно в начале урока.
Например, в качестве мотивационной задачи для задач на «выделение объектов из фона» можно использовать тест на сложные фигуры, содержащие в своем составе простые фигуры. Можно предложить найти простую фигуру (рис. 7) в составе сложной фигуры (рис. 8) и выделить ее другим цветом. При этом получится изображение, представленное на рис. 9.
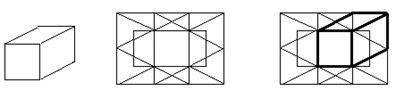
рис. 7. рис. 8. рис. 9.
Для того чтобы учащиеся поупражнялись в перецентрировании, можно предложить им найти все четыре параллелепипеда на чертеже, каждый раз выделяя их другим цветом (для этого понадобятся несколько однотипных изображений сложной фигуры.
Кроме того, возможна ситуация, когда основная задача оказывается непосильной для учащихся. Проблема, как правило, связана с тем, что у учащихся либо не хватает знаний для решения задачи, либо задача перенасыщена деталями (загруженный чертеж, большое количество ситуации, к которым применимо условие задачи и т.д.). В первом случае (если, например, задача содержит термин, недостаточно знакомый учащимся) применяется задача на актуализацию знаний. Важно чтобы в процессе работы с такой задачей происходило выявление и коррекция субъектного опыта учащихся, связанного с недостаточно освоенным материалом [10]. Если же проблема связана с тем, что основная задача перенасыщена деталями, то применяются подготовительные и вспомогательные задачи. Как подготовительная, так и вспомогательная задача является упрощением основной задачи. Причем, одна и та же задача может быть и подготовительной, и вспомогательной. Все зависит от ее местоположения. Подготовительная задача дается до предъявления основной задачи, а вспомогательная – после предъявления основной задачи. Целесообразность данной методики определяется следующим: для того чтобы учащиеся успешно решали задачи на «перецентрирование», необходимо чтобы они, работая с текстом задачи, научились составлять вспомогательные задачи-упрощения основной задачи. Для обучения этому учитель применяет подготовительные и вспомогательные задачи. Подготовительную задачу составляет сам учитель, если он предполагает, что основная задача вызовет затруднения у учащихся. Вспомогательная задача составляется после предъявления основной задачи в процессе совместной работы учителя с детьми с тем, чтобы впоследствии дети научились при необходимости самостоятельно составлять такие задачи. Так, если работа с загруженным чертежом вызывает затруднения у учащихся, необходимо предлагать им подготовительные и вспомогательные задачи, позволяющие работать с менее загруженным чертежом.
Еще одним принципом, которому должна удовлетворять система задач на «перецентрирование» является определенная последовательность задач в системе. В нашем случае это означает, что при работе с определенным понятием сначала изучаются задачи, соответствующие первому и второму виду дивергенции, а только потом задачи, соответствующие третьему и четвертому виду дивергенции. Задачи на первый и второй вид дивергенции даются на этапе введения нового материала. Задачи на третий и четвертый вид дивергенции даются на этапе повторения.
Например, задачи на «выделение объекта из фона» целесообразно предлагать на этапе введения и первичного закрепления понятия. При введении определения новой фигуры (независимо от того, индуктивным или дедуктивным способом это делается) предлагается набор задач на распознавание. В этот набор целесообразно включать задачи на «выделение из фона», используя при этом загруженные чертежи. Работу с задачами на распознавание целесообразно проводить в два этапа. На первом этапе предлагать простые чертежи, содержащие одну фигуру, по поводу которой нужно определить, принадлежит она объему некоторого понятия или нет. На втором этапе можно предлагать загруженные чертежи, их сложность должна постепенно увеличиваться. Такой чертеж должен содержать несколько фигур, принадлежащих объему изучаемого понятия.
Выводы
В ходе опытно-экспериментальной работы были определены пути развития дивергентного мышления через систему задач на перецентрирование, включающую несколько подсистем. С задачами каждой организуется определенная работа, что позволит достичь общей цели – развития дивергентного мышления учащихся и одновременно будет способствовать обучению учащихся решению задач по планиметрии.
Рецензенты:
Снегурова В.И., д.п.н., профессор, зав. кафедры методики обучения математике и информатике РГПУ им. А.И.Герцена, г. Санкт-Петербург;
Татьяна С.Б., д.п.н, профессор, директор научно-образовательного центра «Ломоносовский институт», профессор кафедры педагогики САФУ им. М.В.Ломоносова, г. Санкт-Петербург.
Библиографическая ссылка
Калинова Ю.А., Подходова Н.С. СИСТЕМА ЗАДАЧ НА «ПЕРЕЦЕНТРИРОВАНИЕ» КАК СРЕДСТВО РАЗВИТИЯ ДИВЕРГЕНТНОГО МЫШЛЕНИЯ // Современные проблемы науки и образования. 2015. № 6. ;URL: https://science-education.ru/ru/article/view?id=23362 (дата обращения: 04.11.2025).



