Современный этап развития экономики страны характеризуется потребностью в научных и инженерных кадрах, способных реализовывать инновационные технологии с опорой на естественно-научные знания. Это меняет тренды современного школьного образования, которое на современном этапе призвано подготовить инициативных личностей, способных учиться, творчески мыслить, находить нестандартные решения в сложных ситуациях, владеющих навыками критического мышления. Концепция преподавания учебного предмета «Физика» в образовательных организациях Российской Федерации, реализующих основные общеобразовательные программы, предлагает следующие направления достижения этой цели: «реализация деятельностного подхода к оценке учебных достижений, усиление роли качественных задач, увеличение доли заданий практико-ориентированного характера…» [1]. Направленность деятельностного подхода в обучении на формирование умения учиться, готовности к активной познавательной деятельности соответствует содержанию подготовки школьников к решению олимпиадных задач по физике. Под олимпиадной задачей будем понимать нестандартную задачу повышенной сложности, обладающую новизной и оригинальностью, в условии которой описаны модели научных задач, решение которых возможно различными способами.
Цель исследования состоит в разработке способа формирования познавательной самостоятельности школьников в процессе решения олимпиадных задач по физике.
Материал и методы исследования
Анализ содержания олимпиадных заданий, предлагаемых учащимся на разных уровнях и видах олимпиад по физике, позволил установить, что все олимпиадные задачи, независимо от уровня олимпиады, отличаются от типовых школьных задач. Главной отличительной особенностью олимпиадных задач по физике является нестандартность, хотя для решения таких заданий требуется применить знания в объеме школьных курсов физики и математики. При этом решение олимпиадных физических задач требует умения строить физические модели, глубокого понимания физических законов, умения самостоятельно применять их в различных ситуациях, а также свободного владения математическим аппаратом [2]. Сформировать у школьников готовность к участию в физических олимпиадах возможно лишь при систематическом обучении их решению нестандартных расчетных и экспериментальных задач при изучении конкретных тем. Для этого на уроках физики и при обучении на специально организованных образовательных площадках (лицейские классы при университете, курсы, клубы по подготовке к решению олимпиадных задач) учащиеся учатся решать не только задачи с явно заданной физической моделью, но и задачи, подразумевающие самостоятельное создание физической модели, адекватной условиям задачи, осваивают методы самостоятельного планирования и проведения экспериментов.
Результаты исследования и их обсуждение
Неотъемлемой частью процесса обучения физике является такой вид деятельности, как решение задач, который позволяет сформировать «представления о физической сущности явлений природы, овладеть научным подходом к решению различных задач, умением формулировать гипотезы, конструировать, оценивать полученные результаты» [3]. При решении физических задач у школьников расширяется диапазон физических знаний, развиваются мотивация к учению, познавательная самостоятельность, воспитывается трудолюбие, упорство в достижении поставленной цели.
Школьные физические задачи по степени сложности можно классифицировать на учебные, исследовательские и олимпиадные. Олимпиадные и исследовательские задачи, в отличие от учебных, являются нестандартными, так как не имеют однозначного способа решения. Каждая задача представляет собой определенную проблему, предполагающую проведение самостоятельного теоретического или эмпирического физического исследования. Умение решать олимпиадные задачи характеризует высокое качество знаний учащихся. В то же время олимпиадная задача является инструментом определения уровня сформированности познавательной самостоятельности личности.
Согласно Н.А. Половниковой, познавательная самостоятельность представляет собой «готовность (способность и стремление) своими силами вести целенаправленную познавательную деятельность», которая опирается на имеющиеся у учащегося знания и на владение способами выполнения деятельности [4]. Т.И. Шамова рассматривает познавательную самостоятельность с позиции воспитания положительных мотивов к учению, формирования системы знаний и способов деятельности по их применению и приобретению новых [5]. По мнению И.Я. Лернера, познавательная самостоятельность показывает сформированность у учащихся стремление и умение познавать в процессе целенаправленного творческого поиска. Формой ее проявления является решение учащимися задачи, представляющей проблему, самостоятельное решение которой приводит к новым знаниям и способам решения [6].
На основании проведенных в течение многих лет исследований отечественных и зарубежных ученых можно заключить, что познавательная самостоятельность личности формируется при выполнении нестандартных, творческих заданий [7-9]. Таким образом, можно утверждать, что вовлечение школьников в деятельность по решению олимпиадных задач позволяет сформировать у них высокий уровень познавательной самостоятельности.
Для формирования познавательной самостоятельности учащихся необходимо осуществить подбор олимпиадных заданий, удовлетворяющих определенным требованиям:
- система олимпиадных заданий должна способствовать развитию логического мышления путем самостоятельного применения математических и физических знаний в нестандартных ситуациях. Необходимо, чтобы задания повышали качество имеющихся у учащегося предметных знаний и формировали новые;
- система олимпиадных заданий должна обеспечивать систематичность их выполнения, разнообразие деятельности обучающихся и соответствовать изучаемому материалу. При разработке системы заданий необходимо, чтобы предыдущее задание являлось основой для выполнения следующего задания. Задания необходимо выстраивать от простого к сложному. Каждое задание формирует определенное умение, система заданий в целом направлена на систему умений учащихся;
- система олимпиадных заданий должна стимулировать самостоятельное исследование, выбор метода решения задачи, разработку способа решения задачи;
- система олимпиадных заданий, формирующих познавательную самостоятельность учащихся, должна творчески развивать ученика;
- в систему олимпиадных заданий обязательно должны входить экспериментальные задания [9]. Простейшим вариантом такого задания может служить лабораторная работа, при выполнении которой необходимо измерить ту или иную физическую величину, используя конкретное оборудование. При этом учащийся самостоятельно должен спланировать эксперимент, провести измерения, обработать полученные экспериментальные данные и оценить точность полученных результатов.
При построении системы олимпиадных заданий, способствующих формированию познавательной самостоятельности учащихся, подбираются такие задания, которые подводят ученика к необходимости самостоятельно думать, рассуждать, принимать решения. Несмотря на то что региональный и заключительный этапы Всероссийской олимпиады школьников проводятся только для 9-11 классов, систематическую подготовку школьников к решению олимпиадных задач целесообразно начинать уже в 7 классе. К тому же младшие школьники имеют возможность участвовать не только в местных олимпиадах, но и в олимпиаде имени Максвелла - общероссийском соревновании по физике для школьников 7-8 классов, заменяющем региональный и заключительный этап Всероссийской олимпиады школьников.
Анализ материала, изучаемого в курсе физике 7 класса, позволил установить возможность обучения школьников способам решения олимпиадных заданий с самого начала изучения физики. Рассмотрим систему олимпиадных заданий по теме «Гидростатика» для учащихся 7-9 классов, соответствующих приведенным выше требованиям, в которых рассматривается поведение тел, погруженных в жидкость. В задачах такого типа часто требуется определить изменение уровня жидкости в цилиндрическом сосуде с вертикальными стенками при разных условиях погружения тела. При решении таких задач мы предлагаем научить учащихся нестандартному методу решения, который предполагает составление динамического уравнения не для тела, плавающего в жидкости, а для всего содержимого сосуда. Такой метод известен в физике под названием «метод весов».
На основе анализа заданий, предлагаемых на различных этапах Всероссийской олимпиады школьников по физике в разные годы, нами составлена и апробирована система олимпиадных заданий, обучение решению которых позволяет сформировать высокий уровень познавательной самостоятельности школьника. Согласно теории деятельности, усвоение метода решения происходит при его многократном применении (7-8 раз) в различных ситуациях [10]. Поэтому предлагаемая система заданий включает 7 задач, часть из которых (задачи 1-3) требует выполнения деятельности «вручную», с применением оборудования. Задачи по теме «Гидростатика» могут быть подобраны из сборников задач по физике повышенного уровня сложности [11], заданий различных этапов Всероссийской олимпиады школьников по физике, размещенных в сети Интернет [12], статей, посвященных обучению школьников методам решения физических задач нетрадиционными способами [13; 14]. Необходимость подготовки школьников к решению экспериментального тура потребовала включения в систему заданий задач, требующих проверить результат, полученный из расчета, экспериментом. Приведем пример формулировки такой задачи.
Задача 1. Предскажите, изменится ли (и если да, то как) уровень воды в цилиндрическом стакане, если находящийся в воде лед полностью растает. Сконструируйте экспериментальную установку и проверьте полученный результат экспериментально.
В систему заданий также необходимо включать задачи, решение которых возможно несколькими способами. Рассмотрим пример задачи, решение которой возможно нестандартным «методом весов», а также выделим действия, входящие в его содержание.
Задача 2. В цилиндрическом сосуде с площадью дна 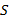 с помощью нити удерживают под водой кусок льда, внутри которого имеется воздушная полость. Объём льда вместе с полостью равен
с помощью нити удерживают под водой кусок льда, внутри которого имеется воздушная полость. Объём льда вместе с полостью равен 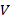 , плотность льда
, плотность льда 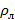 . После того как лёд растаял, уровень воды в сосуде уменьшился на
. После того как лёд растаял, уровень воды в сосуде уменьшился на 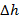 . Найдите объём
. Найдите объём 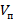 воздушной полости [12].
воздушной полости [12].
Решение задач такого типа возможно с применением «метода весов», включающего действия:
1. Изобразить графическую модель ситуации, описанной в задаче, для двух состояний жидкости и погруженного в неё тела (в начале и конце опыта).
2. Построить физическую модель ситуации задачи.
3. Записать второй закон Ньютона для всего содержимого сосуда для выделенных состояний.
4. Сравнить и записать уравнения для силы давления на дно сосуда в начале и конце опыта.
5. Сравнить количество неизвестных физических величин и количество уравнений. В случае необходимости записать дополнительные уравнения.
6. Решить полученную систему уравнений относительно искомой величины.
7. Оценить полученный результат на достоверность (при возможности провести экспериментальное исследование с целью проверки правильности полученного теоретического результата) [15].
Применим данный обобщенный метод для решения задачи № 2.
На рисунке изобразим графическую модель ситуации задачи для первого и второго состояния воды и погруженного в неё куска льда с полостью.
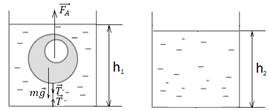
Графическая модель ситуации задачи № 2
Пусть 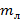 - масса льда,
- масса льда, 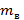 - масса воды в сосуде,
- масса воды в сосуде, 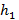 - уровень этой жидкости в состоянии 1,
- уровень этой жидкости в состоянии 1, 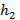 - ее уровень в состоянии 2 после таяния льда,
- ее уровень в состоянии 2 после таяния льда, 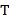 – сила натяжения нити.
– сила натяжения нити.
Вес содержимого сосуда и сила давления столба жидкости в состояниях 1 и 2 будут равны соответственно:
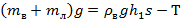 (1)
(1)
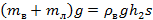 (2)
(2)
Приравняем правые части уравнений (1-2) и выразим Т:
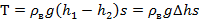 (3)
(3)
Запишем II закон Ньютона для куска пористого льда в проекции на ось, направленную вертикально вниз:
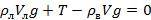 , (4)
, (4)
где 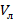 – объем льда в куске.
– объем льда в куске.
Подставим в уравнение (4) выражение (3) для Т:
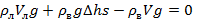
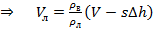 (5)
(5)
Найдем значение объёма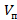 воздушной полости
воздушной полости
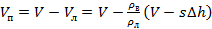 . (6)
. (6)
Для освоения обобщенного способа решения олимпиадных заданий учащимся необходимо многократно применить его для решения конкретных задач, выстроенных по мере усложнения. Предыдущая задача должна быть промежуточной по отношению к цели деятельности. Отличительной особенностью разработанных нами по конкретным темам систем олимпиадных заданий является нацеленность на последовательное формирование высокого уровня познавательной самостоятельности.
Обучение школьников через последовательную отработку действий методами для решения разработанных систем олимпиадных заданий позволяет обучающимся последовательно и углубленно осваивать содержание физики, развивая у них познавательную самостоятельность. Результатом такой работы является повышение успеваемости школьников, развитие мотивации к олимпиадному движению. Школьники перестают бояться принимать участие в олимпиадах разного уровня. Авторы статьи на протяжении многих лет организуют работу по подготовке школьников к олимпиадам, разрабатывают задания Прикаспийской межрегиональной олимпиады школьников по физике, проводимой Астраханским государственным университетом, вовлекая в образовательный процесс все большее количество учеников.
Заключение. Подготовка школьников к решению олимпиадных задач позволяет не только выявить и подготовить талантливых детей, но и сформировать у них высокий уровень познавательной самостоятельности, навыки мышления, умение выбирать оптимальный путь решения. Несомненно, можно включать олимпиадные задания в контекст урока, однако сделать это в рамках часов, отведенных на преподавание предмета, крайне сложно. Для успешного формирования познавательной самостоятельности школьникам необходимо дополнительно заниматься, учиться решать олимпиадные задания. В связи с этим необходимо введение дополнительных общеразвивающих программ, факультативов, элективных курсов, направленных на развитие у школьников мотивации к углубленному изучению физики, формирование познавательной самостоятельности. Включение практикума по решению олимпиадных задач в учебный процесс позволяет сформировать у учащихся высокий уровень познавательной самостоятельности. Повышение уровня сложности заданий от простого к сложному, выход за рамки школьной программы позволяет постепенно расширить кругозор учащегося и стимулировать его к самостоятельному поиску решения задач, сформировать личностную потребность к успеху в академических достижениях.
Библиографическая ссылка
Валишева А.Г., Крутова И.А., Амантаева Л.С. РЕШЕНИЕ ОЛИМПИАДНЫХ ЗАДАНИЙ ПО ФИЗИКЕ КАК СРЕДСТВО ФОРМИРОВАНИЯ ПОЗНАВАТЕЛЬНОЙ САМОСТОЯТЕЛЬНОСТИ ШКОЛЬНИКОВ // Современные проблемы науки и образования. – 2020. – № 6. ;URL: https://science-education.ru/ru/article/view?id=30314 (дата обращения: 26.04.2024).



