Портфельное инвестирование призвано максимизировать доходы вкладчика, сокращая риски финансовых потерь. Снижение риска происходит за счет диверсификации вложений. Такое распределение средств формирует инвестиционный портфель - множество ценных бумаг, каждая из которых может принести определенную прибыль или убыток[1]. Оценка эффективности портфеля складывается из совокупности составляющих его акций. Причем идет усреднение как риска, так и прибыли. Если бы задача ставилась в четко определенных условиях, то решение было бы связано с выбором наиболее доходных акций. Однако существующая ситуация связана с множеством рисков:
- процентный риск связан с изменением уровня процентных ставок;
- риск ликвидности связан с невозможностью продажи акции в нужный момент времени по соответствующей цене;
- рыночный риск отражает проявление рыночных факторов, которые оказывают влияние на вложения всех видов;
- отраслевой риск связан с особенностями и разным уровнем развития определенных отраслей.
Оценка доходности акций также неоднозначна. На нее может влиять множество факторов, поэтому задача решается в условиях существенной неопределенности. Подобный класс задач сводится к получению множества решений, учитывающих многообразие возможных исходов. Причем каждое из решений может привести к нескольким исходам. Для выделения оптимального решения необходимо найти компромисс между неоднозначностью прогноза доходов и убытков от портфельных вложений.
Суть портфельного инвестирования состоит в улучшении возможностей инвестирования путем придания совокупности объектов инвестирования тех инвестиционных качеств, которые недостижимы с позиции отдельно взятой ценной бумаги. Ожидаемая доходность акции и ее инвестиционный риск обычно являются параметрами, прямо зависящими друг от друга.
Математическая формализация задачи нахождения оптимальной структуры портфеля ценных бумаг была предложена Г. Марковицем [5].
При применении модели Марковица используются следующие показатели [2].
- Доходность ценной бумаги.
- Риск ценной бумаги.
- Статистическая оценка коэффициента корреляции между показателями доходности двух ценных бумаг.
- Доходность портфеля ценных бумаг.
- Риск портфеля ценных бумаг.
Решением задачи Марковица является множество неулучшаемых портфелей, то есть таких, в которых ожидаемая доходность не может быть увеличена без увеличения риска и, наоборот - риск не может быть уменьшен без уменьшения ожидаемой доходности.
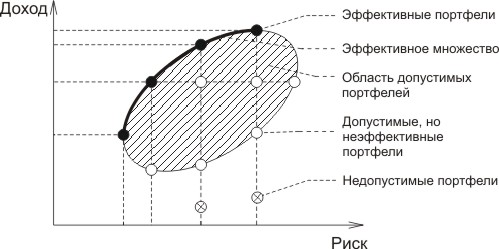
Рис. 1. Допустимое и эффективное множества акций.
На рисунке 1 в виде точек приведено несколько акций в пространстве «риск - доход». Из них выделено множество гарантированно лучших. Они составляют множество Парето. Именно они должны составлять портфель. Принцип допустимости акций определяется на основе заданной минимальной доходности акции.
Проектирование алгоритмов формирования портфеля
Поиск оптимального варианта портфеля по методу Марковица включает в себя следующий порядок действий.
- Вычисление ожидаемой доходности и риска каждой рассматриваемой акции.
- Вычисление коэффициентов корреляции для каждой пары рассматриваемых акций.
- Генерация возможных вариантов портфеля для рассматриваемых акций и вычисление его характеристик.
- Выбор оптимального варианта инвестиционного портфеля, согласно поставленным условиям.
Основываясь на изложенной последовательности действий, реализуем алгоритм, формирующий варианты портфеля простым перебором (рис. 2).
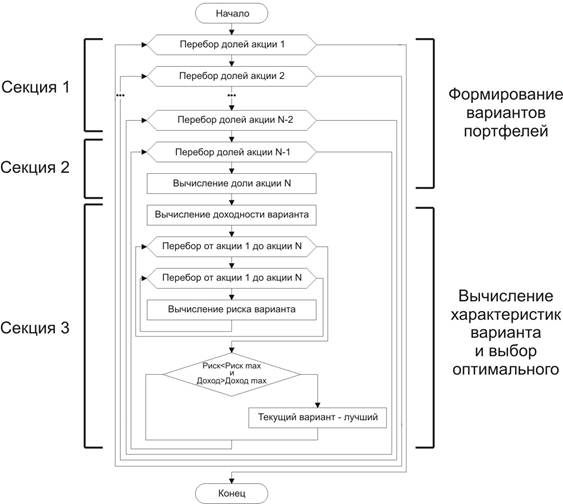
Рис. 2. Формирование вариантов портфеля и выбор оптимального решения.
Под перебором долей акции в данном алгоритме подразумевается изменение процентного соотношения акций в портфеле. То есть перебор долей по каждой акции охватывает диапазон от 0 до 100%. Таким образом, очередной вариант портфеля образуется путем взаимного изменения долей какой-либо пары акций. Естественно, не анализируются варианты портфелей, сумма долей акций которых не равна 100%.
Рассмотрим пример численного решения задачи. Используем данные, полученные с сайта www.finam.ru за период январь - апрель 2012 г. [4]. На основании этих данных подсчитываем доходность для шести акций. Используя полученные доходности, просчитаем риски вложения в каждую рассматриваемую акцию, а также коэффициенты корреляции для каждой пары акций. Необходимо сформировать портфель, который имел бы риск менее 9% и в то же время обладал максимально возможной доходностью. Это означает, что мы максимизируем доходность при граничном условии. Условием является среднеквадратичное отклонение ожидаемой доходности не более 9%. Риск учитывает исторический разброс доходности и корреляций акций.
Алгоритм реализовывался на основе технологии .NET Framework 3.5. Вычислительные эксперименты производятся на персональном компьютере с процессором AMD Phenom2 x4 920 и тактовой частотой 2.8 Ггц, 3 Гб оперативной памяти. Используется операционная система Windows Seven Professional SP1. Для первого вычислительного эксперимента выберем шаг в 1%. Результаты выполнения: время - 166 секунд, доходность - 4,71%, риск - 8,99%.
Время формирования оптимального портфеля велико даже для составления набора из небольшого количества акций. О диалоговом взаимодействии с автоматизированной системой на базе вышеприведенного алгоритма не может быть и речи. А так как время расчета пропорционально факториалу количества акций, то существует близкий потолок, при котором время расчета становится критическим. Результат расчета теряет свою актуальнось, например, для мониторинга существующего портфеля. Время генерации оптимального варианта превосходит время, отведенное на принятие решения. Следует внести изменения в расчет для сокращения времени вычислений.
Одним из способов сокращения количества рассматриваемых вариантов является увеличение шага при переборе долей акций. Реализуем формирование вариантов портфеля, используя шаг в 4%. В этом случае мы не рассматриваем множество близких вариантов портфеля. Однако, за счет гладкости функции доходности портфеля в зависимости от процентного распределения долей акций, полученное решение должно быть близким к предыдущему. Результат выполнения программы: время - 0,28 секунды, доходность - 4,68%, риск - 8,95%.
Шаг в 4% существенно сократил время расчета при незначительном снижении результативности. Для повышения качества решения добавим в расчет поиск в окрестностях найденного результата. Алгоритм используется тот же (рис. 3), но с ограничением по нижней и верхней границам. Верхняя и нижняя границы определяются соответственно как текущий результат плюс/минус шаг перебора (4%). Результат работы поиска портфеля с последовательным снижением шага дает следующие результаты: время - 0,32 секунды, доходность - 4,71%, риск - 8,99%.
Текущий результат совпадает с результатом первого эксперимента, но время вычислений сокращается более чем в 700 раз. Для шести акций время анализа теперь приемлемо для диалоговых систем. Однако с ростом числа рассматриваемых акций время получения решения опять возрастет.
В качестве наиболее быстрого способа синтеза оптимального портфеля можно использовать метод половинного деления шага для последовательного приближения к оптимальному варианту. Однако этот подход не спасет ситуацию с ростом числа акций. Необходимо рассмотреть дополнительные способы увеличения скорости получения решения. Например, путем распараллеливания вычислений. Задачи с большей размерностью нужно решать с расчетом нескольких предварительных вариантов портфеля одновременно. Чем большее число параллельных потоков поддерживает аппаратное обеспечение, тем быстрее сформируется портфель.
Оценим количественно увеличение скорости вычислений при распараллеливании алгоритма. При 4 аппаратных потоках AMD Phenom2 x4, теоретическая граница увеличения производительности алгоритма стремится к 4 при уменьшении времени синхронизации до 0. Однако ответ на вопрос насколько влияет синхронизация потоков на сокращение теоретического ускорения получим практическим путем.
Реализуем следующий вариант распараллеливания: один поток формирует варианты портфеля, а вычисление их характеристик производится с помощью других потоков. Данный способ разделения деятельности между потоками позволит хорошо масштабировать решение на компьютерах с разным числом активных потоков. Для реализации параллельных вычислений используем технологию пула потоков на базе .NET Framework 3.5. Данный подход наиболее производительный и гибкий с точки зрения автоматического управления многопоточностью в рамках .NET [3].
Очередная модификация алгоритма заключается в том, что основной поток программы формирует варианты портфелей и размещает их в очередь для расчета потоками пула. Таким образом, каждый вариант портфеля рассчитывается в отдельном потоке. Вычислительный эксперимент при шаге в 1% дает результат за время - чуть большее 8 минут.
Накладные расходы на формирование очереди и передачу данных от одного потока к другому (синхронизация) значительно превышают потенциальное ускорение от параллельной обработки данных. Полученный результат хуже однопоточного.
Для сокращения очереди запросов к пулу потоков и операций по синхронизации уменьшаем количество формируемых заданий к пулу. Для этого увеличиваем нагрузку на каждый расчетный поток за счет формирования пакетов из нескольких вариантов портфеля. Модификация алгоритма заключается в следующем.
Выделим секции 2 и 3, показанные на рис. 2, в функцию расчета в потоке пула. Рассмотрим результат работы модифицированной программы, используя данные по шести акциям и шаг в 1%. Время - 75 секунд вместо 166 секунд в последовательном варианте программы.
В таблице 1 приведено время работы последовательного и параллельного вариантов алгоритма с разным первоначальным шагом. Данные наглядно представлены на рис. 3.
Таблица 1 - Время работы разных вариантов алгоритма
|
Количество акций |
Парал. шаг=2%, (с) |
Парал. шаг=4%, (с) |
Парал. шаг=5%, (с) |
Парал. шаг=10%, (с) |
Посл. шаг=2%, (с) |
Посл. шаг=4%, (с) |
|
6 |
2,43 |
0,53 |
0,53 |
0,53 |
6,34 |
0,31 |
|
7 |
3,95 |
0,88 |
0,65 |
0,53 |
10,24 |
1,42 |
|
8 |
15,21 |
4,26 |
1,13 |
0,53 |
39,06 |
6,48 |
|
9 |
67,55 |
15,67 |
15,67 |
0,56 |
175,49 |
26,48 |
|
10 |
322,43 |
68,92 |
11,83 |
0,63 |
838,32 |
94,78 |
|
11 |
- |
162,18 |
38,64 |
0,8 |
- |
328,05 |
|
12 |
- |
451,39 |
121,99 |
1,02 |
- |
1148,75 |
|
13 |
- |
1361,88 |
356,4 |
1,49 |
- |
3540,32 |
При разработке систем, формирующих портфель по методу Марковица, необходимо широко использовать как методы численной оптимизации, позволяющие сократить количество вычислений, так и различные способы распараллеливания этих вычислений. При параллельной обработке необходимо уделять особое внимание синхронизации потоков. Так как расчетные потоки не взаимодействуют между собой, нужно рассматривать только вопрос о способе генерации вариантов портфеля и передачи их в параллельные потоки для расчета.
Так как нагрузка на основной поток меньше, он генерирует вариант решения с большей скоростью, чем расчетный поток дает оценку этому варианту. Поэтому для сокращения числа заданий в очереди основной поток должен периодически засыпать, отдавая свои вычислительные ресурсы расчетным потокам. Такой способ позволит выполнять балансировку нагрузки между генератором вариантов портфеля и расчетными потоками.
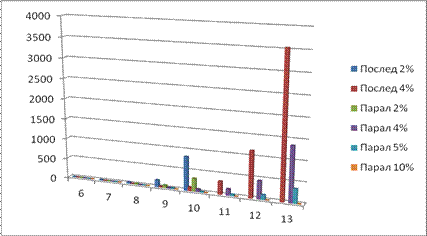
Рис. 3. Время работы разных вариантов алгоритма.
Заключение
Анализ рисунка 3 показывает, что не всегда мультипоточность ускоряет решение задачи. В случае маленького числа акций накладные расходы на организацию нескольких вычислительных потоков превышают потенциальное ускорение от параллельного анализа вариантов портфеля. Однако в случае большого числа акций достоинства многопоточной обработки несомненны.
Ускорить получение результата можно увеличив шаг поиска. Однако данное решение дает предварительный грубый ответ. В ряде случаев этот ответ может быть достаточен для условий задачи. Ведь расчет в условиях риска основывается на средних показателях доходности. Небольшие отклонения от оптимального усредненного варианта в ту или иную сторону для каждой акции склонны взаимно компенсироваться. Но для учета таких эффектов требуется разработать более сложную математическую модель.
Рецензенты
- Лукьянов В.С., д.т.н., профессор, зав. кафедрой «ЭВМ и системы», Волгоградский государственный технический университет, г. Волгоград.
- Муха Ю.П., д.т.н., зав. кафедрой «Вычислительная техника», Волгоградский государственный технический университет, г. Волгоград.
Библиографическая ссылка
Кузнецов М.А., Авдюхин А.В. АЛГОРИТМ ФОРМИРОВАНИЯ ИНВЕСТИЦИОННОГО ПОРТФЕЛЯ НА ОСНОВЕ МЕТОДА МАРКОВИЦА И ЕГО ОПТИМИЗАЦИЯ ПО СКОРОСТИ ВЫПОЛНЕНИЯ // Современные проблемы науки и образования. – 2012. – № 3. ;URL: https://science-education.ru/ru/article/view?id=6399 (дата обращения: 26.04.2024).



