Материал и методы исследования
1. Введение
Многофазные системы массового обслуживания (СМО) с непрерывной загрузкой достаточно широко исследованы в литературе, поскольку используются для моделирования производственных и вычислительных систем. В большинстве случаев рассматривалась двухфазная система с надежными, например [7], и ненадежными [6] приборами, с конечными промежуточными накопителями между приборами [9]. В [8; 10] оценивалась пропускная способность марковских систем, состоящих из пяти и более приборов с неидентичными временами обслуживания. Однако уже А.К. Эрланг для решения практических задач был вынужден отказаться от показательного распределения времени обслуживания. Действительно, если считать, что время обслуживания распределено по показательному закону, то «распределение длительности оставшейся части работы по обслуживанию не зависит от того, сколько оно уже продолжалось» [13]. Но это противоречит физической природе процесса обслуживания. Чем дольше обслуживание длится, тем быстрее оно закончится.
Наибольшие успехи достигнуты по процесссам с экспоненциальным распределением продолжительностей. В этом случае представляющие собой процесс функционирования линейные дифференциальные уравнения составляют по схеме процессов, используя элементарные формальные правила [2]. Если продолжительности не подчиняются экспоненциальному распределению, возникают серьезные трудности как в описании процесса, так и в решении уравнений, которыми бывают дифференциальные уравнения в частных производных, интегро-дифференциальные или интегральные уравнения, которые характеризуются вычислительной неустойчивостью.
Для исследования систем предлагается метод условных вероятностей (МУВ), разработанный для изучения случайных процессов, непрерывных во времени и дискретных по состояниям. В [1; 3] метод был применен для получения характеристик надежности систем с запасными элементами, в [11] - для изучения двухстадийных процессов. В этих же работах было представлено сравнение значений характеристик процессов, рассчитанных по МУВ и по известным формулам для случая экспоненциального распределения длительностей, составляющих случайный процесс.
2. Описание метода
В настоящей работе с использованием МУВ исследуются характеристики следующей системы обслуживания:
- многофазная система состоит из надежных (не отказывающих) последовательно расположенных приборов без промежуточных накопителей между ними;
- заявки поступают на первый прибор непрерывно;
- время Ti обслуживания заявки i-м прибором случайно и характеризуется функцией распределения произвольного вида F(ti);
- система функционирует в течение некоторого отведенного времени TО, которое может быть как детерминированным, так и случайным c функцией распределения FO(t).
Метод условных вероятностей состоит из двух этапов. Первым этапом является схематизация общего процесса функционирования системы. Схема включает в себя состояния и переходы между ними. Каждому состоянию присваивается номер. Состояния представляются составом длительностей одновременно протекающих процессов обслуживания. Если процесс ограничен отведенным временем, то оно будет представлять состояние как любая другая длительность с той лишь разницей, что с его окончанием все остальные частные процессы приостанавливаются с остаточными длительностями. Так, для исследуемой системы (рис. 1) исходное, нулевое, состояние определяется двумя процессами: обслуживанием первой заявки на первом приборе и течением отведенного времени, что соответственно на рисунке обозначено 11 и О; буква Т опущена.
Состояние прекращается с истечением одной и только одной длительности, что является основным принципом схематизации. При этом общий процесс переходит в другое состояние, что на схеме обозначается стрелкой. У стрелки в скобках записывается обозначение длительности, окончание которой в предыдущем смежном состоянии обусловило рассматриваемое состояние. Принципиальным отличием от схем, представленных в [2; 12], является односторонность переходов, что позволяет исследовать показатели системы за интересующий промежуток времени.
Метод учитывает реально образующиеся состояния системы вследствие завершения обслуживания заявки на конкретном приборе или окончания отведенного времени. В результате исходное множество однотипных систем разделяется на соответствующие подмножества. Так, исходное состояние 0 (нулевое) отражает обслуживание в отведенном времени первой заявки на первом приборе у множества однотипных систем. Далее это множество распадается на два подмножества. Первое образуют системы, в которых завершилось обслуживание первой заявки на первом приборе до окончания отведенного времени. Второе подмножество составят системы, в которых первая заявка не была обслужена на первом приборе до окончания отведенного времени. В первом случае общий процесс перейдет в состояние 1, во втором - в состояние 0* и завершится.
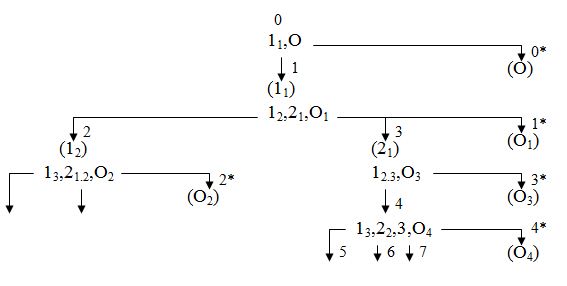
Рис. 1. Начало схемы процесса функционирования в отведенном времени многофазной системы с непрерывной загрузкой.
Состояние 1 характеризуется обслуживанием первой заявки на приборе 2 (обозначено 12) и обслуживанием второй заявки нa первом приборе (обозначено 21) в течение остаточного отведенного времени TО.1. Окончание любого обслуживания или отведенного времени обуславливает переход системы из состояния 1. Так, если время обслуживания на приборе 2 меньше, чем длительности T1 и TО.1, общий процесс перейдет в состояние 2.
Схема не только наглядно показывает разделение исходного множества систем на подмножества, но и указывает на возникновение в процессе функционирования различных длительностей. Так, возникает длительность, связанная с окончанием отведенного времени до завершения времени обслуживания на первом приборе. На ее существование указывает стрелка, ведущая из состояния 0 в состояние 0*. Если отведенное время является детерминированной величиной, то эта длительность, очевидно, равна tO. Также существует длительность обслуживания, завершившегося до окончания отведенного времени, на что указывает стрелка, ведущая из состояния 0 в состояние 1.
В исходном состоянии 0 времена обслуживания известны (заданы). В последующих смежных состояниях обслуживания, не закончившиеся на предыдущих приборах, будут характеризоваться остаточными временами обслуживания. Вторым этапом метода является расчет функций распределения остаточных длительностей, времени пребывания системы в состояниях, приведенных на схеме, а также вероятностей переходов. Именно метод, позволяющий находить эти функции, коренным образом упрощает решение задач, связанных с рассматриваемыми процессами.
Алгоритм расчета функции распределения остаточного времени обслуживания.
1. Из множества процессов обслуживания, представляющих состояние k, выделяется процесс ik, связанный с прибором, на котором закончилось обслуживание. Процесс ik характеризуется известной функцией распределения времени обслуживания ![]() . Для прибора j, на котором обслуживание не закончилось, необходимо найти функцию распределения
. Для прибора j, на котором обслуживание не закончилось, необходимо найти функцию распределения 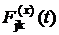 остаточного от состояния k времени обслуживания для следующего состояния х; Fjk(t) - функция распределения времени обслуживания заявки прибором j в состоянии k.
остаточного от состояния k времени обслуживания для следующего состояния х; Fjk(t) - функция распределения времени обслуживания заявки прибором j в состоянии k.
2. Вычисляется функция распределения времени работы z приборов, представляющих состояние k без приборов ik и jk:
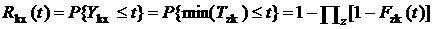 .
.
3. Для прибора ik находится условная функция распределения времени обслуживания, которое меньше времени обслуживания группы приборов, представляющих состояние k без приборов ik и jk:
![]()
где 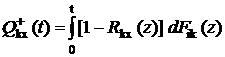 .
.
4. Функция распределения остаточного от состояния k времени обслуживания прибором jk в состоянии х
![]()
где 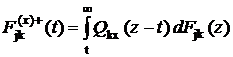 .
.
Для того чтобы и далее вычислялись все показатели для состояния х, переобозначим 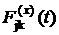 в Fjx(t), аналогично, как и для состояния k.
в Fjx(t), аналогично, как и для состояния k.
Проверочные соотношения для состояния k:
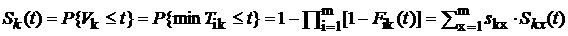 ,
,
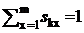 ,
,
где х - номер состояния, смежного с состоянием k.
Произвольное состояние k характеризуется длительностями Vkx пребывания системы в этом состоянии при условии завершения первым каждого по отдельности обслуживания ik из числа всех обслуживаний, представляющих это состояние [4]; при этом система перейдет в состояние x. Функция распределения продолжительности Vkx [5]:
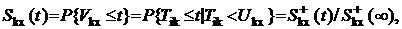 (1)
(1)
где ![]() ;
;
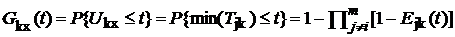 .
.
С вычислением Skx(t) одновременно определяется вероятность перехода системы из состояния k в состояние х:
![]() . (2)
. (2)
3. Численный пример
Для четырехфазной системы обслуживания исследуются показатели, связанные с блокированием системы.
Начало схемы функционирования системы представлено на рис. 1, правая и левая ветви - на рисунках 2 и 3 соответственно.
Расчет показателей начинается с состояния 0, которое характеризуется двумя условными длительностями пребывания в этом состоянии. Условная длительность V0.1 равна времени T1, которое меньше времени TО. Ее функция распределения ![]() вычисляется следующим образом:
вычисляется следующим образом:
![]()
где 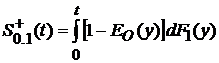 .
.
Соответственно, условная длительность V0.0* - это время TО, которое меньше, чем время T1. Его функция распределения ![]()
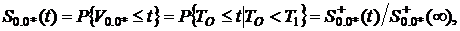
где 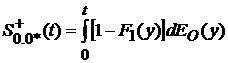 .
.
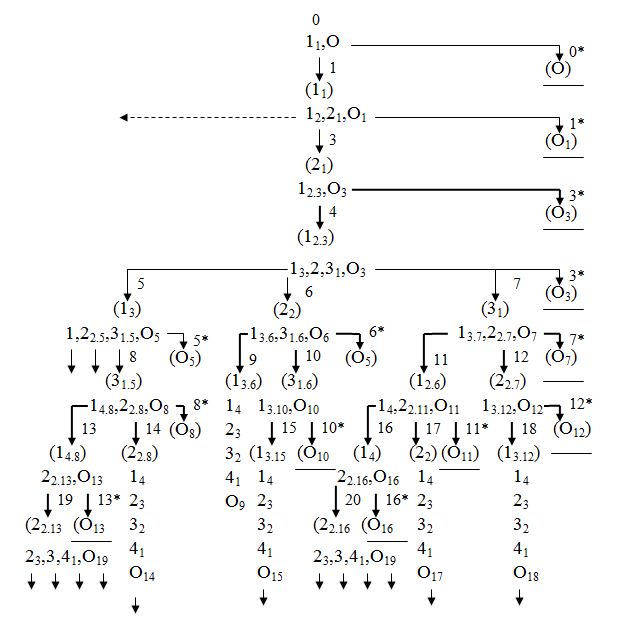
Рис. 2. Схема процесса функционирования в отведенном времени четырехфазной системы с непрерывной загрузкой (правая ветвь).
Соответственно, условная длительность V0.0* - это время TО, которое меньше, чем время T1. Его функция распределения ![]()
![]()
где 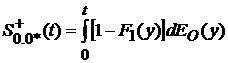 .
.
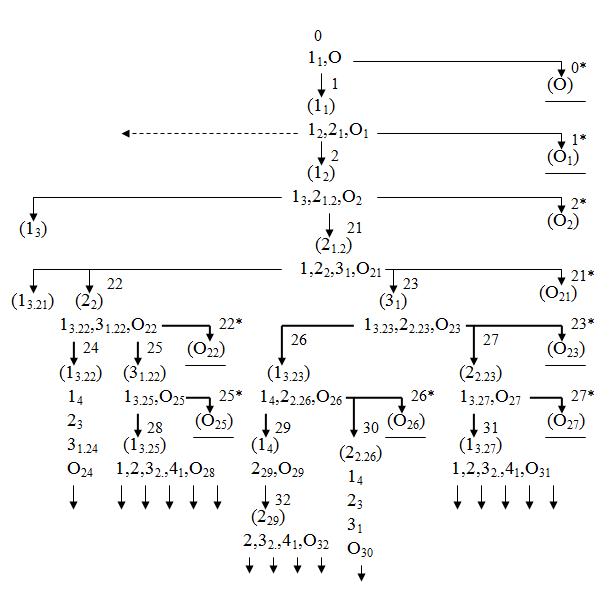
Рис. 3. Схема процесса функционирования в отведенном времени четырехфазной системы с непрерывной загрузкой (левая ветвь).
Вероятность перехода из состояния 0 в состояние 0* - это вероятность того, что время обслуживания T1 меньше отведенного времени TО ![]() . Вероятность перехода из состояния 0 в состояние 1 рассчитывается аналогично -
. Вероятность перехода из состояния 0 в состояние 1 рассчитывается аналогично - ![]() .
.
Если работа системы завершилась в состоянии 0*, остаточное время обслуживания T1.0* вычисляется согласно формальному соотношению 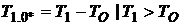 .
.
Во всех последующих состояниях обслуживаниям, которые не закончились к рассматриваемому моменту, свойственна остаточная длительность. Формально остаточное отведенное время в состоянии 1 записывается в виде 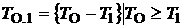 . Его функция распределения
. Его функция распределения
![]() ,
,
где 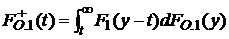 .
.
Время пребывания процесса в состоянии 1 при условии, что первым закончится обслуживание первой заявки на втором приборе, определяется из формального соотношения ![]() . Его функция распределения
. Его функция распределения
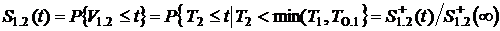 ,
,
где 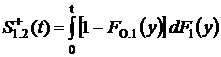 .
.
Время пребывания процесса в состоянии 1 при условии, что первым закончится обслуживание второй заявки на первом приборе - 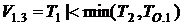 . Время пребывания процесса в состоянии 1 при условии, что первым закончится остаточное отведенное время ТО.1 -
. Время пребывания процесса в состоянии 1 при условии, что первым закончится остаточное отведенное время ТО.1 - 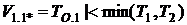 .
.
Вероятности перехода в каждое состояние:
![]() ,
, 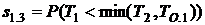 ,
,
 .
.
Если функционирование системы завершилась в состоянии 1*, остаточные длительности обслуживания на первом и втором приборах T1.1*, T2.1* рассчитываются согласно формальным соотношениям:
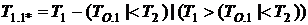 ,
,
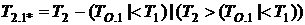 .
.
Рассмотрим состояние 3. Оно характеризуется остаточным временем обслуживания первого объекта на втором приборе T2.3 и остаточным отведенным временем TО.3. Формальные соотношения для их расчета:
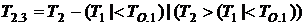 ,
,
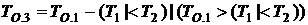 .
.
Функция распределения времени TО.3
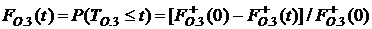 ,
,
где 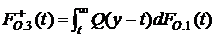 ,
,
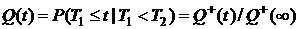 ,
, 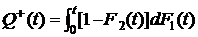 .
.
Функция распределения времени T2.3 вычисляется аналогичным образом.
После расчета остаточных длительностей обслуживания нетрудно вычислить условные длительности пребывания в состоянии V3.6, V3.3* и вероятности перехода ![]() ,
, ![]() . Эти величины определяются формальными соотношениями
. Эти величины определяются формальными соотношениями
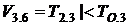 ,
, ![]() ,
,
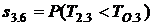 ,
, ![]() .
.
Функции распределения длительностей V3.6, V3.3* рассчитываются по (1), вероятности переходов - по (2).
Состояние 3 обусловлено завершением обслуживания второй заявки на первом приборе. Поскольку на втором приборе продолжается обслуживание первой заявки, вторая заявка блокирует первый прибор. Таким образом, вероятность первой блокировки первого прибора в течение заданного времени ![]() , ее длительность
, ее длительность ![]() .
.
Все блокировки, которым соответствуют состояния системы, находящиеся на схеме ниже ветви 0→3, будут вторыми по счету блокировками в течение отведенного времени. Переходы, обозначающие условные длительности состояний, в которых приборы блокированы, для наглядности выделены более толстыми линиями. Рассмотрим состояния 6 и 22. Они обусловлены окончанием обслуживания второй заявки на втором приборе. Поскольку на третьем приборе обслуживается заявка, то вторая заявка блокирует второй прибор. Однако эта блокировка не оказывает влияния на обслуживание следующей, третьей по счету заявки, которая продолжает обслуживаться на первом приборе. Такие блокировки могут учитываться либо не учитываться в зависимости от решаемой задачи. Состояния 10, 12, 24, 26 отражают состояния системы, в которой блокированы одновременно два прибора, в частности первый и второй.
Таким образом, с использованием метода условных вероятностей можно вычислить:
- вероятность s1 того, что какой-либо прибор будет блокирован, по крайней мере, один раз в течение отведенного времени (первая блокировка): ![]() ;
;
- вероятность ![]() того, что в системе произойдет блокировка двух приборов одновременно (двойная блокировка):
того, что в системе произойдет блокировка двух приборов одновременно (двойная блокировка): ![]() ;
;
- вероятность s2 того, что в системе произойдет не менее двух несмежных блокировок приборов: 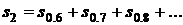 ;
;
- вероятность ![]() того, что вторая по счету блокировка будет двойной:
того, что вторая по счету блокировка будет двойной: ![]() .
.
Средняя длительность ![]() первой блокировки:
первой блокировки:
где 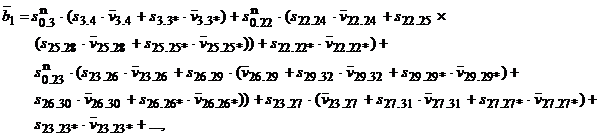
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Средняя длительность ![]() первой блокировки двух приборов одновременно:
первой блокировки двух приборов одновременно:
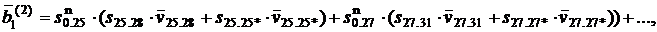
где ![]() ,
, ![]() ,
, ![]() .
.
Средняя длительность ![]() второй несмежной блокировки:
второй несмежной блокировки:
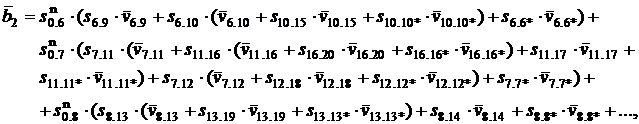
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Средняя длительность ![]() второй по счету одновременной блокировки двух приборов:
второй по счету одновременной блокировки двух приборов:
![]() ,
,
где ![]() ,
, 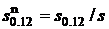 ,
, ![]() .
.
Метод позволяет не только детально рассмотреть функционирование системы обслуживания, но и достаточно быстро сделать выводы о работе системы. Так, первая блокировка определяется, в частности, вероятностью s1.3 (![]() ), которая вычисляется как
), которая вычисляется как ![]() . Поэтому, если система обслуживания допускает перестановку приборов, для уменьшения вероятности блокировки необходимо их располагать в порядке убывания среднего времени обслуживания. К такому выводу можно прийти и путем логических рассуждений, но для реальных систем важно знать, например, насколько эффективна такая перестановка.
. Поэтому, если система обслуживания допускает перестановку приборов, для уменьшения вероятности блокировки необходимо их располагать в порядке убывания среднего времени обслуживания. К такому выводу можно прийти и путем логических рассуждений, но для реальных систем важно знать, например, насколько эффективна такая перестановка.
Рассмотрим две многофазные системы, состоящие из четырех приборов, время обслуживания на которых подчиняется распределению Вейбулла с функцией распределения ![]() . Параметры распределения были выбраны таким образом, чтобы распределение времени обслуживания на каждом приборе отличалось по форме.
. Параметры распределения были выбраны таким образом, чтобы распределение времени обслуживания на каждом приборе отличалось по форме.
Параметры распределения времени обслуживания в системе 1:
λ1=9,2·10-4, α1=2; λ2=9,1·10-10, α2=5; λ3=4,4·10-7, α3=3,66; λ4=1,2·10-1, α4=1. Соответственно, средние времена обслуживания: 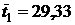 ,
, ![]() ,
, ![]() ,
, ![]() .
.
Параметры распределения времени обслуживания в системе 2:
λ1=9,1·10-10, α1=5; λ2=4,4·10-7, α2=3,66; λ3=9,2·10-4, α3=2; λ4=1,2·10-1, α4=1, средние времена обслуживания: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Результаты расчетов сведены в таблицу 1.
Таблица 1 - Показатели систем обслуживания, связанные с блокированием постов
|
|
Система 1 |
Система 2 |
||||
|
tO |
100 |
200 |
300 |
100 |
200 |
300 |
|
s1 |
0,9218 |
0,9968 |
0,9972 |
0,1059 |
0,5530 |
0,5904 |
|
|
28,06 |
34,07 |
34,36 |
8,52 |
14,05 |
14,47 |
|
|
0,0025 |
0,0152 |
0,0154 |
7·10-6 |
0,0082 |
0,0089 |
|
|
8,20 |
14,18 |
14,62 |
4,96 |
9,32 |
10,92 |
|
s2 |
0,2565 |
0,8848 |
0,8885 |
0,0002 |
0,1472 |
0,1612 |
|
|
16,35 |
37,10 |
38,24 |
5,97 |
14,57 |
16,42 |
|
|
0,0258 |
0,2886 |
0,2944 |
5·10-6 |
0,0142 |
0,01589 |
|
|
9,26 |
15,84 |
16,37 |
4,87 |
10,87 |
10,92 |
Из данных таблицы наглядно видно изменение значений характеристик, связанных с блокированием системы, во времени. Причем для системы 1 показатели, связанные с первой блокировкой (s1, ![]() ,
, ![]() ), к моменту времени ТО=300 можно считать установившимися. Система 2 к этому моменту времени еще находится в переходном режиме.
), к моменту времени ТО=300 можно считать установившимися. Система 2 к этому моменту времени еще находится в переходном режиме.
Данные таблицы также свидетельствуют о том, что перестановка приборов существенно влияет на показатели блокирования. Например, вероятность и длительность первой блокировки существенно снижаются, особенно для промежутка ТО=100. Для ТО>100 средняя длительность первой блокировки для системы 2 снижается более чем в два раза. Если такие изменения существенны для СМО, а перестановка приборов невозможна, то необходимо направленное изменение времени обслуживания на приборах путем проведения специальных мероприятий.
4. Выводы
- Новый метод условных вероятностей для многофазных систем массового обслуживания с непрерывной загрузкой на первом приборе, функционирующей в отведенном времени, позволяет исследовать нестационарное поведение СМО, характеризующейся произвольно распределенными длительностями обслуживания.
- Метод может применяться для исследования многофазных систем к СМО с периодической загрузкой, когда на первый прибор поступает поток заявок (в этом случае длительность интервала между поступлениями заявок добавляется в начальное состояние), с возможностью расчета показателей, характеризующих блокирование системы.
- Универсальность метода (каким бы ни был процесс, он описывается набором одних и тех же соотношений) обусловливает легкость программирования задачи на ЭВМ.
Рецензенты
- Гузеев Виктор Иванович, доктор технических наук, профессор, зав. кафедрой «Технология машиностроения», ФГБОУ ВПО «Южно-Уральский государственный университет» (НИУ), Россия, г. Челябинск.
- Бухтиярова Татьяна Ивановна, доктор экономических наук, профессор кафедры «Бухгалтерский учет и анализ хозяйственной деятельности», ФГБОУ ВПО «Всероссийский заочный финансово-экономический институт» филиал, г. Челябинск.
- Щукин Олег Семенович, д.э.н., доцент, профессор кафедры экономики труда и основ управления, ФГБОУ ВПО «Воронежский государственный университет», г. Воронеж.
Библиографическая ссылка
Королькова Л.И., Переверзев П.П. ОПТИМИЗАЦИЯ ПРОЦЕССОВ ПРЕДПРИЯТИЯ НА ОСНОВЕ НОВОЙ МЕТОДИКИ РАСЧЕТА ХАРАКТЕРИСТИК МНОГОФАЗНОЙ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С НЕПРЕРЫВНОЙ ЗАГРУЗКОЙ БЕЗ ПРОМЕЖУТОЧНЫХ НАКОПИТЕЛЕЙ // Современные проблемы науки и образования. – 2012. – № 3. ;URL: https://science-education.ru/ru/article/view?id=6424 (дата обращения: 27.04.2024).



