Введение
Пневматический транспорт (ПТ) сыпучих материалов, благодаря таким преимуществам перед другими видами транспорта, как экологичность, чистота, доступность в загруженных пространствах, нашел широкое применение в различных отраслях промышленности.
В настоящее время применение пневмотранспорта в различных технологических процессах сдерживается рядом объективных причин. Одной из них является отсутствие единого научного обоснования процесса пневмотранспорта и, как следствие, отсутствие общей методики расчета и конструирования пневматических транспортных установок. Это объясняется сложностью физических явлений, происходящих при пневматическом транспортировании материалов (в трубопроводе обычно используются турбулентные воздушные потоки, которые сами по себе еще далеко не изучены, особенно области течения вблизи стенок трубопровода), разнообразием пневмотранспортных операций и разнородностью транспортируемых материалов.
В настоящее время существуют десятки расчетных методик различных авторов. Их можно классифицировать по типу рассчитываемого оборудования, по видам перемещаемого материала, по отраслям промышленности, где используется оборудование и т.д.
Методы, используемые в строительной отрасли, создавались и отрабатывались на основе экспериментальных исследований транспортирования отдельных материалов (чаще всего цемента) на определенных установках. Поэтому они основываются на эмпирических зависимостях и расчетных формулах. Последние включают опытные коэффициенты, функции которых не определены, а их числовые значения у разных авторов различаются. Применение подобных методик ограничено диапазоном параметров и условий, для которых производились эксперименты. Какими бы масштабными ни были экспериментальные исследования, на основе которых были получены опытные коэффициенты, последние не могут учитывать все многообразие факторов, способных оказывать влияние на процесс пневмотранспортирования. Ввиду этого достоверность, при наличии малейших различий исходных данных и внешних условий, очень низка.
Наибольший интерес здесь представляют работы М. Д. Барского, А. А. Надеина, М. П. Калинушкина, В. Ф. Крамского, М. М. Шапунова, В. С. Серякова, И. П. Малевича и др.
На основании анализа работ приведенных выше авторов можно сформулировать (условно) «классическую» теорию расчета пневмотранспортных установок.
Основные зависимости «классической» теории расчета получены для движения одиночной частицы в ламинарном или турбулентном потоке и тем или иным способом распространяются на движение дисперсной среды двухкомпонентного потока. Основными допущениями здесь являются следующие:
- распределение частиц по сечению материалопровода равномерное;
- концентрация твердого компонента исключает взаимодействие между частицами;
- влияние частиц на движение несущей среды не учитывается.
Такой подход достаточно слабо отражает процессы, происходящие в пневмотранспортных системах.
Немаловажное влияние на достоверность результатов, получаемых при расчетах по этой теории, оказывает превалирование эмпирического подхода. Для упрощения расчетов рекомендуется использовать графики и номограммы, определяющие многочисленные опытные коэффициенты, использующиеся в уравнениях. Таким образом, при изменении исходных данных точность и достоверность расчетов, проведенных по этой методике, априори снижена.
Однако проведение экспериментальных исследований при изменении исходных данных нельзя считать панацеей ввиду их сложности, длительности и высокой стоимости.
В связи с широким распространением вычислительной техники и пакетов программ, позволяющих производить решение сложных систем уравнений, стала широко развиваться область математического эксперимента. Однако при проведении подобных экспериментов важным фактором становится выбор исходных уравнений и замыкающих соотношений, позволяющих корректно описать рассматриваемый технологический процесс в широком диапазоне изменения технологических параметров.
Проведение исследований процессов пневматического транспортирования методом математического моделирования позволит выработать научно-обоснованные подходы повышения его эффективности путем анализа динамических процессов, происходящих при перемещении твердых материалов потоком газа.
В настоящее время наиболее перспективным представляется исследование динамики двухфазового потока, основанное на гетерогенной теории, т. е. каждая фаза потока рассматривается самостоятельно.
В рамках этого подхода все существующие на сегодняшний день математические модели двухфазовых потоков можно разбить на два больших типа. Модели первого типа описывают движение несущей газовой фазы и движение множества взвешенных частиц, основываясь на эйлерово-континуальном представлении. Их называют двухжидкостными, поскольку обе фазы рассматриваются как взаимопроникающие континуумы, сосуществующие в каждой точке пространства. Каждая фаза описывается уравнениями континуальной механики. К другому типу моделей относятся модели, основанные на эйлерово-лагранжевом или континуально-дискретном описании движения гетерогенной среды, а именно: уравнения движения газовой фазы решаются в эйлеровой постановке, в то время как движение частиц описывается лагранжевыми уравнениями, которые интегрируются вдоль их траекторий.
Рассмотрим вкратце преимущества и ограничения эйлеровых (двухжидкостных) и эйлерово-лагранжевых моделей описания движения потоков газа с твердыми частицами.
Преимуществом двухжидкостных моделей является использование похожих уравнений для описания движения газовой и дисперсной фаз. Это позволяет использовать большой опыт моделирования однофазных турбулентных течений и применять одни и те же численные методы решения всей системы уравнений. К недостаткам моделей этого типа можно отнести некоторую «потерю» информации о движении отдельных частиц, а также сложности в постановке граничных условий для дисперсной фазы на ограничивающих течение поверхностях. Теперь несколько слов об эйлерово-лагранжевых моделях. Преимуществом данных моделей является получение детальной статистической информации о движении отдельных частиц в результате интегрирования уравнений движения (теплообмена) частиц в известном (предварительно рассчитанном) поле скоростей (температур) несущего газа. Однако с увеличением концентрации дисперсной фазы возникают сложности в использовании эйлерово-лагранжевых моделей. Можно выделить два обстоятельства. Во-первых, рост концентрации приводит к обратному влиянию частиц на параметры несущего газа, и расчеты приходится выполнять в несколько итераций, что осложняет вычислительную процедуру. Во-вторых, с увеличением концентрации возрастает вероятность столкновений частиц между собой, что ведет к запутанности их траекторий. С уменьшением размера частиц использование траекторных методов для расчета их движения также осложняется. Это связано с тем, что для получения корректной информации об осредненных характеристиках дисперсной фазы необходим учет взаимодействия частиц с турбулентными вихрями несущего газа все меньших и меньших размеров. Отмеченное обстоятельство также сильно осложняет процесс вычислений [1].
Среди исследователей гетерогенных потоков нет единого мнения о том, какому из рассмотренных выше методов следует отдать предпочтение.
Одни авторы [2] считают, что описание двухфазных газодисперсных потоков возможно лишь при раздельном описании жидкой и твердой фаз. Т.е. утверждается, что уравнения континуума могут быть составлены только для жидкой фазы, а для твердой - уравнения дискретного типа. Другие [3,5] - делают вывод о том, что применение моделей, основанных на смешанном эйлерово-лагранжевом описании движения газодисперсного потока, требует значительных затрат вычислительного времени на определение нескольких тысяч траекторий отдельных частиц, что затрудняет применение таких моделей в практических расчетах.
Авторы [4] проводили сравнение эйлерового-эйлерового и эйлерового-лагранжевого подходов к моделированию турбулентных течений смеси газа и частиц. Наряду с этим рассматривались два важных аспекта взаимодействия частиц и жидкости: турбулентная дисперсия частиц (влияние турбулентности газовой фазы на частицы) и влияние «модуляции» (влияние частиц на турбулентность газовой фазы). На основе полученных результатов был сделан вывод, что эйлеров-эйлеров подход является более экономичным и дает лучший результат для твердых частиц диаметром d < 200 мкм. Для смесей же газа и частиц, размер которых изменяется вдоль траектории, т.е. предположение о монодисперсности не выполняется, - единственно возможным является применение эйлерово-лагранжевово подхода.
В работе [1] Вараксин А. Ю. делает вывод о том, что «...с ростом концентрации частиц и уменьшением их инерционности использование континуального эйлерового представления для описания динамики дисперсной примеси оказывается предпочтительным», а применение статистических моделей наиболее рационально при изучении турбулентных газодисперсных потоков, содержащих крупные частицы малой концентрации [4].
Таким образом, на основании вышеизложенного можно сделать вывод, что для математического моделирования процессов пневмотранспорта сыпучих строительных материалов с размерами частиц в пределах от 0,02 до 0,3 мм и при концентрациях материала от 50 до 200 кг/кг наиболее эффективно разрабатывать математическую модель, в основу которой положено предположение о том, что дисперсный поток может быть представлен в виде двух взаимодействующих и взаимопроникающих континуумов.
Основные уравнения теории взаимопроникающих континуумов для описания движения двухкомпонентного потока газ - твердые частицы можно записать следующим образом:
Уравнение сохранения масс
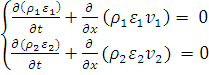 (1)
(1)
Уравнение сохранения импульса
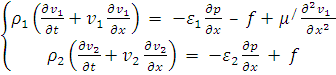 (2)
(2)
Уравнение сохранения энергии
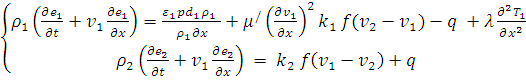 (3)
(3)
Для замыкания системы уравнений записывается уравнение состояния газа
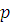 =
=![]() RT1 (4)
RT1 (4)
где ρ - давление потока; ρ1, ρ2 - плотности фаз, индекс 1 соответствует газовой (дисперсионной) фазе, 2 - твердой (дисперсной); ν1, ν2, T1, e1, e2 - скорости, температура и внутренние энергии фаз; ε1, ε2 - объемные доли фаз; R - универсальная газовая постоянная; f - сила межфазного взаимодействия; μ/ - вязкость, которая учитывает эффект присутствия частиц в потоке; q - поток тепла между фазами; λ - коэффициент теплопроводности газа; k1, k2 - коэффициенты, учитывающие долю тепла, возникающую в результате трения.
Для полного замыкания системы уравнений необходимо выбрать модель турбулентности. Не существует универсальной модели турбулентности для широкого диапазона задач. Её выбор зависит от характера турбулентного потока, требуемой точности, доступных вычислительных ресурсов. Кроме этого необходимо поставить физически корректные граничные условия.
Несмотря на сложность систем уравнений (1 - 3), их решение можно получить численными методами. Проведение вычислительного эксперимента позволяет получать необходимые для исследования зависимости. Корректная постановка начальных условий позволяет проследить влияние различных параметров на процесс транспортирования и определить возможность повышения эффективности работы пневмотранспортных систем.
Рецензенты:
- Добромиров Виктор Николаевич, д.т.н., профессор, директор института безопасности дорожного движения, г. Санкт-Петербург.
- Ушаков Алексей Иванович, д.т.н., профессор, директор ООО "Научно-производственный информационно-консультационный центр-плюс", г. Санкт-Петербург.
Библиографическая ссылка
Кузнецова А.А. К ВОПРОСУ О МЕТОДАХ РАСЧЕТА ПРОЦЕССОВ ПНЕВМОТРАНСПОРТА СЫПУЧИХ СТРОИТЕЛЬНЫХ МАТЕРИАЛОВ // Современные проблемы науки и образования. – 2012. – № 3. ;URL: https://science-education.ru/ru/article/view?id=6438 (дата обращения: 26.04.2024).



