Введение. Для обработки и анализа оптических изображений, а также визуализации измерений в настоящее время широко используется представление результатов в трехмерном виде. Применяемые технологии трехмерного сканирования являются весьма трудоемкими и, как правило, требуют ручной доводки получаемых в итоге их применения результатов. Для получения недостающей третьей координаты сканируемого объекта, а именно глубины, в этих технологиях используются либо время задержки отражений лазерного сканирующего луча от объекта, либо степень искажения проекций на сканируемый объект специальной решетки, например решетки в виде полос, смещение соответствующих точек сканируемого объекта на стереоизображениях, либо применяются методы вычисления третьей координаты, основанные на использовании эффекта размытия изображения, обусловленного конечностью глубины фокусировки оптической системы.
Перечисленные методы имеют некоторые ограничения. Лазерные сканеры применяют в настоящее время для сканирования только крупных объектов, таких как здания, вышки, башни, заводские территории, железнодорожные станции, аэропорты и так далее, поскольку погрешность измерения глубины при сканировании небольших объектов оказывается слишком большой.
В другом случае применяется технология, когда на сканируемый объект проецируется специальная решетка в виде полос, схема способа и примеры пространственно модулированной картины приведены на рисунке 1.
а)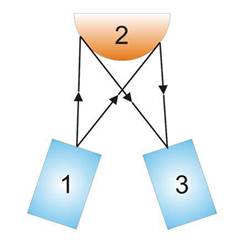 б)
б)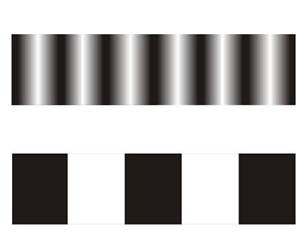
Рис. 1. Способ проекции пространственно модулированной картины на поверхность объекта: а) схема способа, на которой 1 – проектор, 2 – объект, 3 – регистратор изображения; б) примеры пространственно модулированных картин.
В этом способе изображение проецируемое устройством 1 пространственно модулированной подсветки (картины), искаженной поверхностью исследуемого объекта 2, регистрируется с несколькими ракурсами устройством 3, то есть с разным углом между устройствами 1 и 3. Пример искажения пространственно модулированной подсветки приведен на рисунке 2.

Рис. 2. Искажение полусферой проецируемой пространственно модулированной картины, регистрируемой под различными углами.
Возникает проблема сшивания изображений, полученных по нескольким проекциям. Поскольку у реальных объектов различные части имеют сильно различающуюся детализацию, то в областях высокой детальности в создаваемую модель приходится вручную добавлять точки, что делает метод трудоемким. Кроме того, при использовании нескольких камер, либо одной с различными ракурсами, нужно предварительно провести калибровку, то есть определить их взаимное расположение.
Недостаток технологии, основанной на использовании стереоизображений, заключается в том, что при ее применении трудно обеспечить точное соответствие пикселов на изображениях объекта, полученных с двух камер в бесструктурных областях, вследствие чего невозможно обеспечить достаточную точность получаемых трехмерных изображений.
Целью настоящей работы является описание метода и математической модели получения трехмерного изображения исследуемого объекта на основе его собственного поляризованного излучения без использования устройств подсветки объекта либо дополнительных устройств активного сканирования, а также анализ влияния оптических свойств поверхности на способ распознавания формы на основе поляризационных термограмм. Предлагаемая математическая модель получения трехмерного изображения рассматривается при условии, что температура поверхности объекта существенно превышает температуру окружающего фона. Учет влияния окружающего фона, отраженного поверхностью объекта, является отдельной задачей и в данной работе не рассматривается. Для построения трехмерного изображения необходимо иметь значения трех координат элементов поверхности объекта. Две из трех координат определяются размерами матричного фотоприемного устройства тепловизора, а третья координата определяется по ниже описанному методу. Данная математическая модель основана на получении и обработке тепловизионных изображений исследуемого объекта, при этом в оптическую систему вводится вращающийся линейный инфракрасный поляризационный фильтр и используются два поляризационных изображения одной сцены с различными азимутами поляризации, а именно 45 и 90 градусов.
Рассмотрим подробно математическую модель [3].
Известно, что поток излучения можно описать выражением (1):
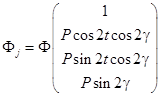 ,(1)
,(1)
где Φ – поток собственного излучения объекта;
Р, t, γ – степень, азимут и степень эллиптичности поляризации теплового излучения объекта;
j = 1, 2, 3, 4.
Данное выражение представляет собой вектор-параметр Стокса, то есть является характеристикой оптического излучения, которая качественно и количественно описывает как энергетические, так и поляризационные свойства излучения объектов [2].
В выражении (1) поток, прошедший через инфракрасный поляризационный фильтр, можно представить в виде [4; 8]:
![]() ,(2)
,(2)
где τij – матрица преобразования Мюллера [2], i = 1, 2, 3, 4.
В предлагаемой модели необходимо обработать две поляризационные термограммы с азимутами поляризации 45 и 90 градусов. Такие термограммы получают путем ввода в оптическую схему тепловизора вращающегося линейного поляризационного фильтра (поляризатора), матрицы пропускания которого для азимутов 45 и 90 градусов соответственно имеют следующий вид [8]:
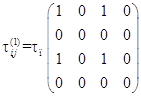 ;(3)
;(3)
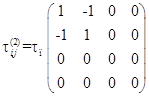 .(4)
.(4)
С учетом этого сигналы, снимаемые с фотоприемного устройства тепловизора, для каждого азимута поляризации, описываются следующими выражениями:
![]() ;(5)
;(5)
![]() .(6)
.(6)
В выражениях (5) и (6) величина U0 равна:
![]() ,(7)
,(7)
где S – чувствительность приемника излучения, который располагается после поляризационного фильтра; τо, τп, τа – соответственно коэффициенты пропускания оптической системы тепловизора, поляризатора и слоя атмосферы между объектом и прибором.
Зависимость степени поляризации собственного излучения элемента поверхности исследуемого объекта от видеосигналов изображения элемента, прошедшего через поляризационный фильтр излучения, с азимутами поляризации 45 и 90 градусов, описывается следующим выражением [5]:
![]() ,(8)
,(8)
где P – степень поляризации излучения; N – номер элемента в строке термограммы; L – номер строки.
Установлено, что степень поляризации собственного оптического излучения поверхности исследуемого объекта меняется в зависимости от угла ориентации участка наблюдаемой поверхности объекта относительно направления ее наблюдения [4]:
![]() ,(9)
,(9)
где Pmax – максимум степени поляризации; y – угол излучения материала поверхности объекта.
С использованием (8), на основании (9), получаем выражение для расчета углов y(N,L):
![]() .(10)
.(10)
При обработке термограмм процесс определения третьей декартовой координаты вдоль линии сканирования осуществляется по формулам [8]:
![]() ;(11)
;(11)
![]() ,(12)
,(12)
где yxy, yxz – соответственно проекции угла y на координатные плоскости XOY и XOZ; ∆yN и ∆zL – шаг сканирования вдоль координат OY и OZ.
В случае анализа поляризационного изображения с комбинированным фильтром в виде последовательно расположенных ахроматической пластинки l/4 с углом ориентации «быстрой» оси Θ=45° и линейного поляризатора с азимутом α=0° зависимость угла ориентации ψ(N,L) от видеосигналов U(N,L) получена в виде [6-7](Здесь и далее с целью удобства записи зависимость угла ψ и видеосигналов U от параметров N и L опущена):
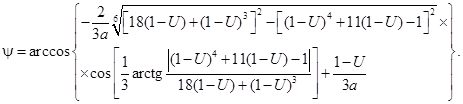 (13)
(13)
Для анализа влияния типа и состояния поверхности исследуемых объектов необходимо учитывать тот факт, что на поляризационные свойства их теплового излучения влияют оптические характеристики материала и шероховатости поверхности исследуемого объекта. При этом предлагается следующая связь между параметрами Pmax, Py, η и поляризованными компонентами коэффициента отражения ρ^ и ρ׀׀ материала поверхности объекта:
![]() ,(14)
,(14)
где
![]() ,(15)
,(15)
где d=2csin(y)tg(y)+sin2(y)tg2(y);
![]() .(16)
.(16)
Для непрозрачных материалов и материалов с комплексным показателем преломления ![]() =n+ik, параметры b2 и c2 равны [1]:
=n+ik, параметры b2 и c2 равны [1]:
![]() ;(17)
;(17)
![]() ,(18)
,(18)
где n, k – оптические постоянные материала поверхности объекта; ψ – угол излучения, при котором наблюдается значение Py степени поляризации теплового излучения материала поверхности объекта; n0 – показатель преломления среды, в котором находится объект; η – коэффициент, зависящий от индикатрисы излучения и шероховатости материала поверхности объекта (η = 1, если высота неровности поверхности h = 0).
Для случая (n2+k2)≫1 (металлы, сплавы) имеем [1]:
![]() ;(19)
;(19)
![]() .(20)
.(20)
Следует отметить, что значение Pmax для конкретного материала получается в том случае, когда в формулах (14)-(18) угол y соответствует значению максимума степени поляризации Py.
На рисунке 3 представлены результаты исследований влияния материала поверхности объекта на значение степени поляризации от угла наблюдения площадки для ряда металлических объектов с гладкой поверхностью.
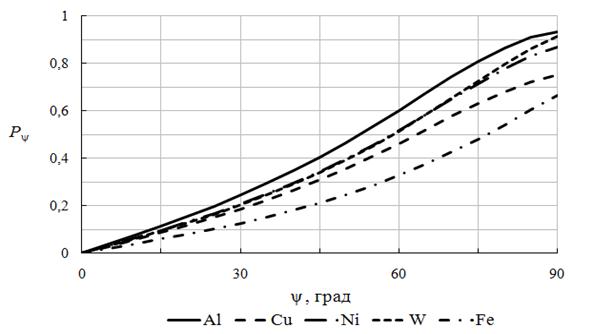
Рис. 3. Зависимость параметра Py от угла ψ собственного излучения для металлических объектов.
Из графиков на рисунке 3 и формул (5) и (6) видно, что материал, из которого выполнен исследуемый объект, оказывает влияние на яркость поляризационных изображений. Как следствие, на основании этих данных и формул (8) и (10) необходимо учитывать влияние оптических свойств поверхности исследуемых объектов на значение угла y для всех (NxL) элементов поляризационных термограмм.
На основе анализа зависимости видеосигналов U1 и U2 элементов поляризационных изображений от ориентации площадки поверхности и с учетом формул (8)-(12) выполнено моделирование и построение трехмерного изображения поверхностей металлических объектов из алюминия в виде сферы, рисунок 4(а) и конуса, рисунок 4(б).
а) б)
б)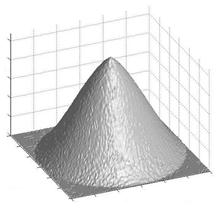
Рис. 4. Результаты моделирования трехмерного изображения объектов.
Заключение. Предложен метод дистанционного определения формы трехмерных выпуклых объектов. Приведены результаты математического моделирования воспроизведения трехмерной формы исследуемого объекта. Приведены результаты расчета влияния материала объекта на степень поляризации его теплового излучения.
Рецензенты:
Айрапетян Валерик Сергеевич, д.т.н., профессор, зав. кафедрой «Специальные устройства и технологии», ФГБОУ ВПО «Сибирская государственная геодезическая академия», г. Новосибирск.
Рахимов Нъематжон Рахимович, д.т.н., профессор кафедры «Специальных устройств и технологий», ФГБОУ ВПО «Сибирская государственная геодезическая академия», г. Новосибирск.
Библиографическая ссылка
Фесько Ю.А. МЕТОД ОПРЕДЕЛЕНИЯ ТРЕХМЕРНОЙ ФОРМЫ ОБЪЕКТОВ НА ОСНОВЕ ПОЛЯРИЗАЦИОННЫХ ТЕРМОГРАММ // Современные проблемы науки и образования. – 2012. – № 6. ;URL: https://science-education.ru/ru/article/view?id=7509 (дата обращения: 26.04.2024).



