Развитие пенсионной системы, основной компонентой которой является обязательное пенсионное страхование, представляет собой ключевую гарантию общества. В связи с увеличением совокупного объема средств пенсионных накоплений, переданных в доверительное управление уполномоченным институтам; нестабильностью финансового рынка и т.п. возникает необходимость развития альтернативных методик и моделей инвестирования средств пенсионных накоплений, которые позволили бы повысить эффективность накопительной компоненты пенсионной системы России. В данной работе авторами предложена модель формирования инвестиционного портфеля пенсионных накоплений с линейным критерием качества и получено ее решение. Предложенная модель проверена на реальных данных.
Постановка задачи
Рассмотрим портфель, состоящий из 
рисковых активов и 
безрисковых активов. Обозначим объемы вложений в момент времени 
в рисковые активы 
(
), а в безрисковые активы – 
(
).
Задача управления заключается в перераспределении капитала между включенными в портфель активами таким образом, чтобы сформированный портфель следовал капиталу эталонного инвестиционного портфеля на горизонте управления 
.
Стоимость инвестиционного портфеля 
в момент времени равна
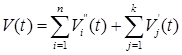. (1)
Заметим, что доля вложения в 
-й рисковый актив в момент времени равна 
, а в безрисковый актив 
.
Динамику капитала рисковой части инвестиционного портфеля в дискретном времени можно описать уравнением [1]
(2)
Здесь 
– капитал, вкладываемый в покупку рискового актива (
) либо вырученный от продажи рискового актива (
); 
– среднее значение ставки -й рисковой ценной бумаги; 
– случайная составляющая ставки рисковой ценной бумаги с параметрами 
, где 
– матрица ковариации доходностей рисковых ценных активов; 
– ставка 
-го безрискового актива. Безрисковая часть портфеля в работе [1] представлена одним активом.
В отличие от работы [1] безрисковый актив мы представляем в виде подпортфеля. Кроме того, предполагаем, что рыночная ставка доходности безрисковых ценных бумаг может изменяться мгновенно для всех периодов на одну и ту же величину. Это обстоятельство приводит к необходимости иммунизации безрискового подпортфеля.
Динамику капитала безрисковой части инвестиционного портфеля в дискретном времени будем описывать уравнением
(3)
Уравнение эталонного портфеля определим уравнением:
(4)
где 
- заданная ставка эталонного портфеля, 
.
Введем векторы 
и 
. Тогда уравнения (2), (3) и (4) можно переписать в виде
, (5)
где 
; 
– диагональные матрицы размерности 
с элементами
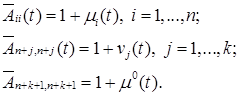
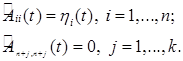(6)
Матрица 
размерности 
имеет структуру
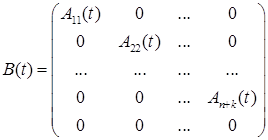. (7)
В качестве целевой функции выберем линейный функционал
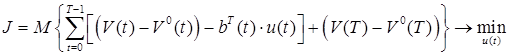, (8)
где 
.
Используя 
, перепишем 
в форме 
, где 
. Критерий качества 
примет вид
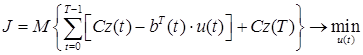. (9)
Итак, имеем задачу оптимального управления, в которой уравнение состояния описывается многошаговым процессом (5), а функционал качества – выражением (9). Управление задается вектором 
. Задача решается при ограничении 
или
. (10)
Ограничение, связанное с запретом продажи без покрытия, имеет вид
. (11)
В терминах ограничение (7) имеет вид
, (12)
где 
– матрица диагональная размерности 
с единичными элементами на главной диагонали и нулевой последней строкой.
Введем ограничения на объёмы вложений в ценные бумаги, определяемые законодательством [5; 6]
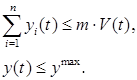(13)
Здесь
– максимально допустимый объем вложений в ценные бумаги; 
– ограничение на объем вложений в рисковые ценные бумаги.
Перепишем эти ограничения в терминах , получим
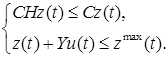(14)
где 
;
– диагональная матрица размерности 
с элементами:
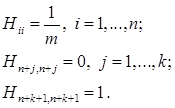
Для иммунизации подпортфеля безрисковых ценных бумаг введем ограничение
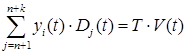, (15)
где 
– дюрация 
-й безрисковой ценной бумаги.
Перепишем (15) через
, (16)
где 
диагональная матрица размерности с элементами:
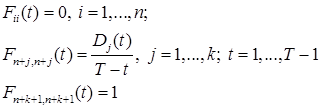
Для решения задачи слежения необходимо задать начальное состояние системы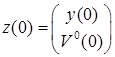 
. Стоимость эталонного портфеля в начальный момент времени считаем известной 
. В качестве 
используем решение задачи [3]
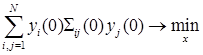, (17)
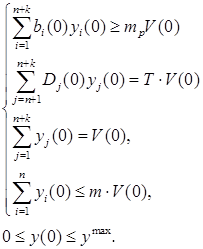(18)
где 
– желаемая доходность портфеля; 
– дюрация безрисковой ценной бумаги.
Итак, сформулируем окончательно задачу управления портфелем.
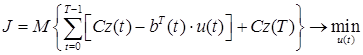, (19)
, (20)
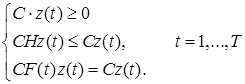(21)
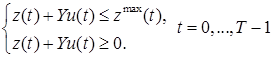. (22)
Решение задачи
Имеем линейную задачу динамического программирования. Ее можно решать методом Беллмана. Однако численная реализация этого метода достаточно трудоемкая задача. Мы будем решать ее другим способом.
Преобразуем нашу задачу к эквивалентной задаче линейного программирования. Подставим (20) в (19) и (21)-(22). Целевая функция примет форму
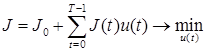, (23)
где
, (24)
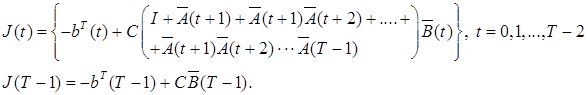(25)
В результате задача слежения примет вид
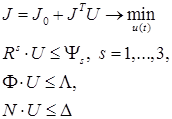(26)
Здесь 
: 
; 
;
; 
; 
.
; ;
;
.
; .
, ;
;
; 
; 
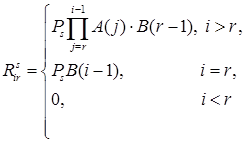
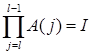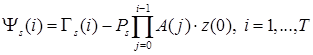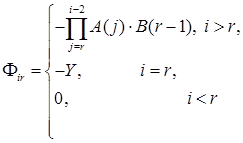
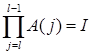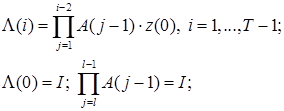
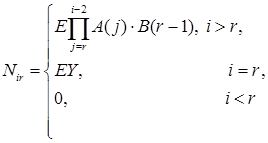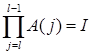
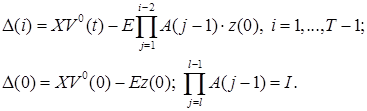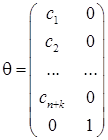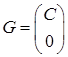
Здесь 
– вектор ограничений на объемы вложений (
).
Итак, мы имеем стохастическую задачу, так как в ограничениях (26) матрицы 
и случайны. Поэтому оптимальное управление будет также случайным. На практике, как правило, именно такая ситуация имеет место.
Алгоритм решения задачи
Задача (26) может быть решена стандартным симплекс-методом с помощью любого математического пакета (например, Mathcad) или компьютерной программы, написанной на языке, например, Fortran, С++, С#. Однако следует отметить, что на практике задачи линейного программирования большой размерности решаются очень плохо. В нашем случае размерность задачи составляет 
, и при 
и 
получим число переменных 100. Для преодоления этой трудности воспользуемся методом управления с прогнозирующей моделью [1].
Суть метода состоит в следующем. Задается горизонт прогнозирования 
. Для заданного начального состояния 
вычисляется последовательность управляющих воздействий 
. На следующем шаге горизонт управления сдвигается на один шаг (
), а в качестве начального состояния берется 
, найденное на предыдущем шаге. Процедура повторяется до тех пор, пока 
, где 
– число шагов. Размерность каждой подзадачи равна 
.
Учет волатильности рисковых ценных бумаг
Волатильность рисковых ценных бумаг будем учитывать с помощью ограничений рискового подпортфеля
. (27)
Введем следующую блочную матрицу
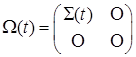размерности .
Здесь 
– матрица ковариации доходностей рисковых активов размерности 
; 
– нулевая матрица размерности 
. Тогда ограничение (27) можно записать в форме
. (28)
Прежде чем решать задачу с учетом ограничения (28), проверяем их выполнение с найденным решением задачи (26). Если ограничения (28) выполняются для всех 
, то в качестве решения оставляем найденное решение задачи (26). Если ограничения (28) для некоторых 
не выполняются, то решаем задачу (26) заново с учетом ограничения (28).
Для сохранения линейности задачи представим 
, где 
– начальное приближение управления, найденное при решении задачи (24) без ограничения (26); 
– добавка. При каждом значении будем линеаризировать ограничение (26). В результате получим
, (29)
где 
;
; 
;
; 
; 
;
;
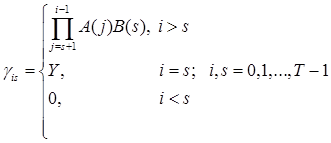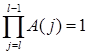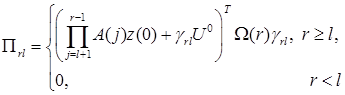
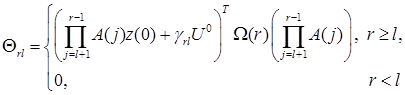Численное моделирование
Получим стратегию управления инвестиционным портфелем пенсионных накоплений, состоящим из облигаций 3 эмитентов: ОАО «АКБ Связь-банк», Самарская область, Министерство финансов РФ; и акций 10 эмитентов: ОАО «ВТБ», ОАО «Сбербанк России», ОАО «Лукойл», ОАО «Газпром», ОАО «Северсталь», ОАО «РусГидро», ОАО «Интер РАО ЕС», ОАО «ФСК ЕС», ОАО «Аэрофлот» ОАО «НК «Роснефть»» [2; 3]. Горизонт инвестирования: с 1 октября 2013 года по 1 октября 2014 года. Шаг пересмотра инвестиционного портфеля выбирается равным одному месяцу. Ниже введем начальные условия.
В начальный момент времени 
руб. Примем дневную доходность эталонного портфеля 
на всем горизонте инвестирования неизменной 
; дюрации облигаций 
, вектор ограничений 
;
- сводный вектор доходностей ценных бумаг; матрица 
.
В результате моделирования получили следующие результаты по управляемому и эталонному инвестиционным портфелям (рис. 1). На оси абсцисс отмечены моменты переформирования портфеля; на оси ординат – совокупный объем портфелей.
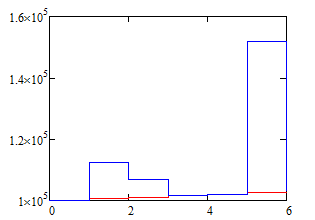
Рис. 1. Динамика управляемого (синяя линия) и эталонного (красная линия) инвестиционных портфелей
По результатам численного моделирования отмечаем, что капитал управляемого портфеля хорошо отслеживает рост капитала эталонного портфеля и преимущественно превосходит его.
Рецензенты:
Арефьев К.П., д.ф-м.н., профессор кафедры высшей математики Томского политехнического университета, г. Томск;
Катаев М.Ю., д.т.н., профессор кафедры АСУ Томского государственного университета систем управления и радиоэлектроники, г. Томск.
Библиографическая ссылка
Мицель А.А., Мицель А.А., Мицель А.А., Рекундаль О.И., Золтоев А.Б. ДИНАМИЧЕСКАЯ МОДЕЛЬ УПРАВЛЕНИЯ ИНВЕСТИЦИОННЫМ ПОРТФЕЛЕМ ПЕНСИОННЫХ НАКОПЛЕНИЙ // Современные проблемы науки и образования. 2015. № 1-1. ;URL: https://science-education.ru/ru/article/view?id=17416 (дата обращения: 04.11.2025).